三角形的外角

江苏省南京市六合区励志学校 孙德萍

一、复习三角形的内角

问题1：如图1，△ABC有几个内角？它们有什么关系？

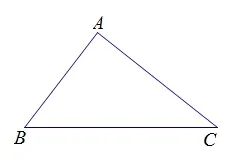
图1

设计意图：通过复习三角形内角的个数和三角形内角和定理，为进一步学习三角形外角的定义和三角形内角和定理的推论作准备。

二、三角形外角的定义

把三角形的一边延长，如图2，得到∠ACD，∠ACD叫作三角形的外角.

问题2：请你画出图中三角形的其他外角，并用自己的语言描述三角形外角的定义.

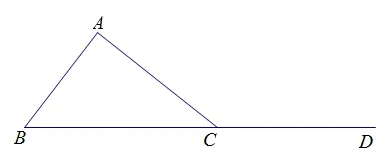
图2

师生活动：教师引导学生根据外角的形成过程，用文字语言给出三角形外角的定义.小组交流，达成共识。

设计意图：让学生通过画图操作，体验外角的形成过程，为进一步归纳三角形外角的定义提供思路，并指出根据三角形内角的个数，我们默认三角形的一个顶点处只算一个外角。

三、三角形内角和定理推论的证明

问题3：观察此图，∠ACD与△ABC的内角有什么数量关系？

师生活动：教师提出问题，学生思考后回答，出现两种数量关系：（1）∠ACD+∠ACB=180°；（2）∠ACD=∠A+∠B。

设计意图：通过观察图形中角与角之间的数量关系，培养学生发现问题和解决问题的能力。

追问1：针对第2 个数量关系，结合图2，你能写出已知、求证和证明吗？

师生活动：一般的思路是用三角形内角和定理结合平角的定义进行证明，教师巡视时，若有学生采用过点C添加平行线的方法，也要给予展示。

设计意图：让学生通过严格的逻辑推理证明“三角形的外角等于与它不相邻的两个内角的和”，进一步感悟几何证明的意义，体会几何证明的规范性。

追问2：你能用文字语言和符号语言概括出这个结论吗？

师生活动：学生回答问题，并相互补充，教师板书，归纳出推论的图形语言、文字语言和符号语言。

设计意图：锻炼学生的口头表述能力和用数学语言概括结论的能力。

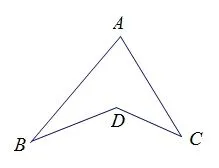
图3

四、巩固三角形内角和定理的推论

例题：如图3，是一个飞镖形ABDC。

求证：∠BDC=∠A+∠B+∠C。

师生活动：学生先思考后独立完成，对有困难的学生可适当提示：把不熟悉的图形转化为熟悉的图形来解决，然后小组交流，并汇报不同的作辅助线的方法和不同的证明思路。一般有三种添辅助线的方法：（1）延长BD交AC于点E；（2）连接并延长AD到E；（3）连接BC。

设计意图：飞镖形是一个非常基本的常见图形，对今后的解题有一定的帮助；通过“割”或“补”的方法，把飞镖形变成两个三角形，体会添加辅助线解决这种不规则图形问题，体现了“转化”的数学思想，丰富学生的解题经验.培养学生的逻辑推理能力.

追问：如果改变点D的位置，这四个角的关系会不会发生变化？请画出图形，写出结论。

师生活动：学生先独立思考画图，再分组讨论，教师深入小组，倾听学生的交流，并帮助、指导学生完成此题，再由一个学生在多媒体上演示点D的位置变化，所得到的不同图形，结论也不一样，总结有以下三种情况：

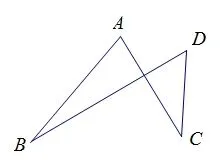
图4

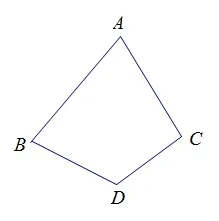
图5

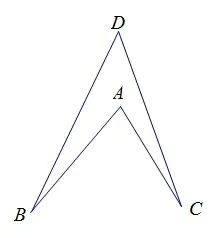
图6

图4 的 数 量 关 系 是：∠A+ ∠B= ∠C+ ∠D；图5 的 数 量关系是：∠A+∠B+∠D+∠C=360°；图6 的数量关系是：∠A=∠B+∠C+∠D。针对每一种情况，让学生进行说理。

设计意图：通过活动鼓励学生在独立思考的基础上，积极地参与到对数学问题的讨论中来，勇于发表自己的观点，学会说理；通过例题的变式，进一步拓展学生的思维.

五、小结

本节课学习了哪些主要内容？

对于外角，你认为后面我们还将学习什么？

师生活动：学生回顾与思考，总结本节课所学知识，教师引导学生回顾，关注学生对外角基本图形的认识。