基于改进卷积神经网络的短时交通流量预测

贾伟，赵雪芬

（宁夏大学新华学院，银川750021）

0 引言

近年来，随着城市化进程的推进和机动车数量快速增加，交通拥堵问题日益严重并成为影响城市发展的重要问题。为了有效解决交通拥堵问题，一些学者提出采用短时交通流量预测的方法解决交通拥堵问题。短时交通流量预测方法通过已经构建的交通流量预测模型预测未来一段时间内的交通流量信息，为交通管理人员和出行人员的交通管理和出行提供参考信息，从而避免交通拥堵。BP 神经网络[1]是一种多层前馈神经网络，由于其具有较好的自学能力、泛化能力和非线性映射能力，成为研究短时交通流量预测的重要方法。由于BP 神经网络选取的初始权值和阈值具有随机性，使得其会出现全局搜索能力较差，易陷入局部最优解和收敛速度较慢的问题。为了克服BP 神经网络的不足之处，在短时交通流量预测中，一些学者利用粒子群优化（Particle Swarm Optimization，PSO）算法[2]和布谷鸟搜索（Cuckoo Search，CS）算法等算法[3]优化BP神经网络的初始权值和阈值，例如，蔡玥[4]提出的改进BP 神经网络IPSO-BP，该方法给出一种自适应变异算子的PSO 算法IPSO，并将其应用于优化BP 神经网络的初始权值和阈值。唐新来等人[5]提出的改进BP 神经网络CPSO-BP，该方法利用混沌PSO 算法CPSO 优化BP 神经网络的初始权值和阈值。高述涛[6]提出的改进BP 神经网络GCS-BP，该方法利用基于高斯扰动的CS算法GCS 优化BP 神经网络的初始权值和阈值。赖锦辉和梁松[7]提出的改进BP 神经网络TCS-BP，该方法利用t 分布的CS 算法TCS 优化BP 神经网络的初始权值和阈值。但是，现有的优化算法对BP 神经网络的初始权值和阈值的优化结果还不够理想。为此，本文拟提出一种改进的BP 神经网络DPSO-BP，利用PSO 算法优化BP 神经网络的初始权值和阈值，提高BP 神经网络的全局搜索能力和收敛速度，从而提高交通流量预测的准确率。考虑到PSO 具有收敛速度快和参数设置较少的优点的同时，还存在易早熟收敛和局部寻优能力较差的问题，本文首先在PSO 算法框架中提出一种改进的PSO 算法，然后利用改进的PSO 算法优化BP 神经网络的初始权值和阈值，并将其应用于短时交通流量预测中。

1 BP神经网络算法

BP 神经网络的拓扑结构如图1 所示，其是由输入层、隐含层和输出层组成，其中，输入层的节点数是A，隐含层的节点数是B，输出层的节点数是Q，各层之间通过神经元相互连接，神经元一般采用Sigmoid 函数作为激励函数，xi是输入层第i 个神经元，输入层到隐含层的权重是wi,j，阈值是θj，隐含层到输出层的权重是λj,k，阈值是θk。

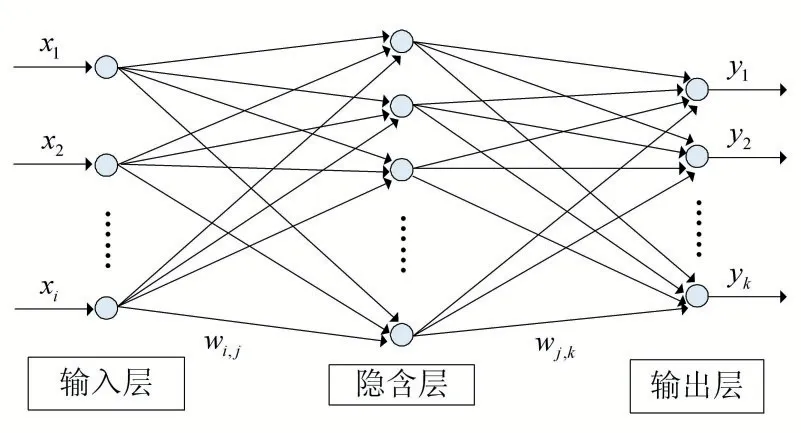
图1 BP神经网络拓扑结构

在隐含层中，第j 个节点的输出值为：

在输出层中，第j 个节点的实际输出值为：

期望值与网络训练后的实际输出值之间的误差由下式得到：

其中，Ok是样本在第k 个输出节点的期望值。

在得到期望值后，若期望值与网络训练后的实际输出值之间的误差较大，就进行反向传播，对各层的权值和阈值进行调整。重复多次正向和反向传播，直到网络输出的误差减小到一定程度或达到最大训练次数为止。反向传播过程中，根据学习速率η，隐含层的权值和阈值的更新分别为：

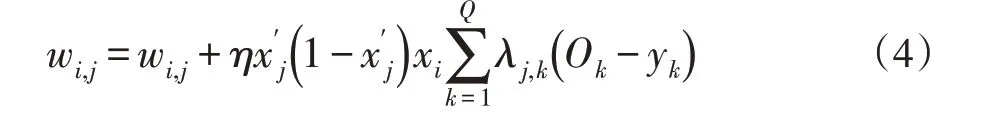
输出层的权值和阈值的更新分别为：

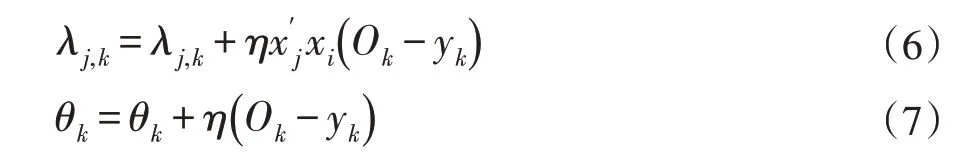
2 改进的BP神经网络

2.1 改进的PSO算法

设粒子的位置是X=( xi,1,xi,2,···,xi,D)，粒子的速度是V=( vi,1,vi,2,···,vi,D)，粒子i 的个体历史最优位置Pi=( pi,1,pi,2,···,pi,D)，整 个 粒 子 群 的 历 史 最 优 位 置Pg=( pg,1,pg,2,···,pg,D)，在D 维空间中，标准的PSO 算法的粒子的速度和位置的更新公式是：

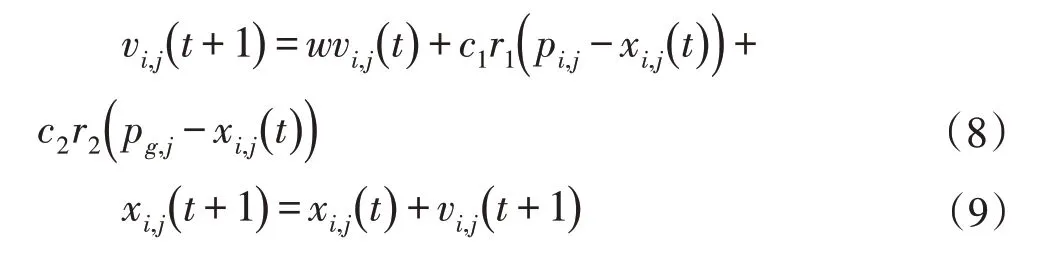
其中，c1和c2是学习因子，r1和r2是[0 ,1] 之间的随机数，w 是惯性因子。

w 的计算公式为：

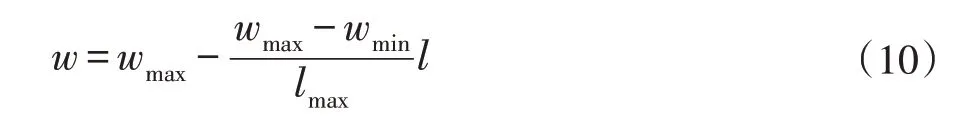
其中，wmax和wmin分别是w 的最大惯性权重和最小惯性权重，lmax是最大迭代次数，l 是当前迭代次数。

为了提高PSO 算法的局部搜索能力收敛性，本文该出一种改进的PSO 算法DPSO，该算法采用双种群搜索的策略，两个种群分别进行独立寻优，将Levy 飞行[8]和元胞自动机[9]分别应用到两个种群的搜索中，并在两个种群的搜索过程中采用差分进化算法提高种群的多样性，最后，在两个种群的最优解中选择最优的粒子作为全局最优解。

Levy 飞行作为一种服从Levy 分布的随机游走方式，可表示为：

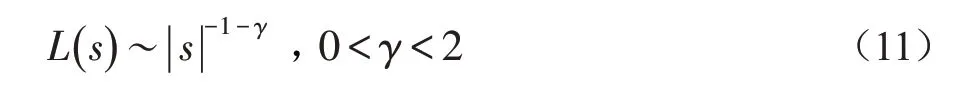
其中，s 为随机Levy 步长，s 由下式计算得到：

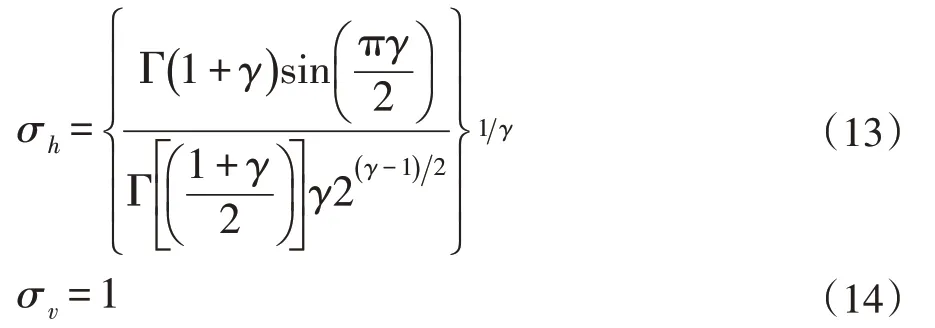
其中，Γ 是标准伽马函数。

引入Levy 飞行后，得到的粒子位置更新公式如下：其中，α 是步长因子，⊕是点乘积，Levy( )γ 是服从参数为γ 的Levy 分布。

元胞自动机是在一个由具有离散、有限状态的元胞组成的元胞空间上建立的动力学系统，本文在粒子群寻优过程中使用的元胞自动机类型是Moore 型。如图2 所示，在Moore 型中，种群中的所有粒子由元胞来表示，黑色的元胞通过与周围灰色的邻居元胞的比较实现元胞的更新。粒子群通过元胞的转换规则在整个子群空间中更新最优粒子。

图2 Moore型

粒子群在二维元胞空间中的描述如下：

（1）每一个粒子都被看成是一个元胞，

（2）粒子i 的位置是元胞的状态，定义为：

（3）粒子i 的邻居定义为：

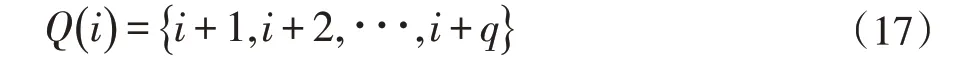
其中，q 是邻居数。

（4）元胞的转换规则为：

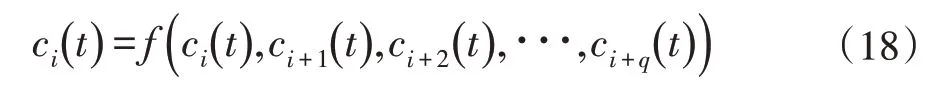
差分进化算法是一种基于群体差异的启发式随机搜索算法，在差分进化算法中，在第t+1 次迭代中，对于 每 一 个 个 体 yi(t)={yi1(t),yi2(t),···yij(t)}(i ∈{1,2,···,NP})，变异个体由下式得到：

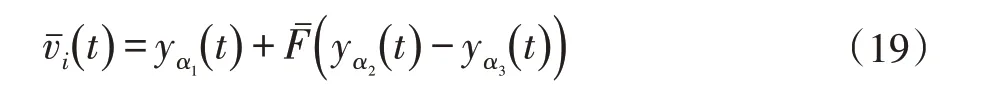
其中，α1、α2和α3，是随机正整数，Fˉ是缩放因子。

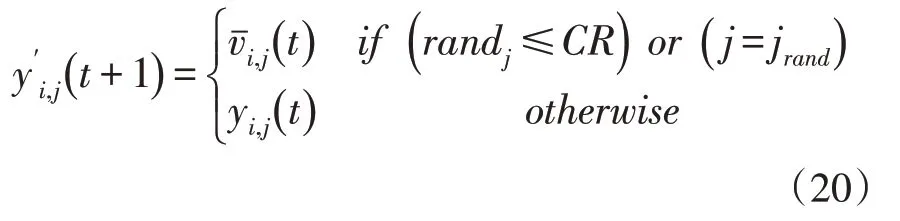
其中，randj是之间均匀分布的随机数，CR是变异概率，jrand是随机选择指数。

如图3 所示，在本文提出的改进的PSO 算法中，首先将种群随机划分为两个种群W1和W2，将Levy 飞行和元胞自动机分别应用到两个种群的搜索中。当两个种群找到最优解后，分别在两个种群中采用差分进化算法[10]对当前种群进行变异，得到两个变异种群CW1和CW2，将W1和CW1，S1和CW2进行比较，选取最优粒子组成两个新的种群NW1和NW2。在种群W1和W2寻优结束后，从两个种群中选取最优解作为全局最优解Pg。

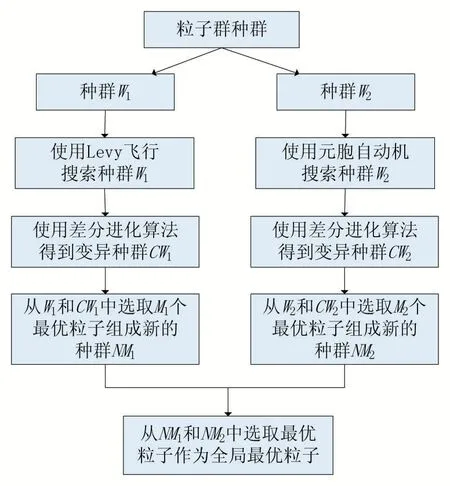
图3 改进的PSO算法

改进的PSO 算法描述如下：

算法1 改进的PSO 算法

输入：粒子的最大速度vmax，最大惯性权重wmax，最小惯性权重wmin，最大迭代次数Tmax，学习因子c1和c2，随机数r1和r2，邻居数q ；

输出：全局最优粒子；

begin

将当前种群随机划分为两个大小为M1的种群W1和W2；

对于种群W1，计算初始种群每个粒子的适应度函数值，得到粒子的历史最优位置和种群的最优位置；

while（g ≤gmax）

利用式（10）计算w；

for i=1 to M1do

for d=1 to D do

if rand ＜0.5

利用式（9）更新粒子的速度；

利用式（10）更新粒子的位置；

else

利用式（9）更新粒子的速度；利用式（15）更新粒子的位置；

end if

end for

end for

利用式（19）和式（20）对当前种群进行变异，得到新的种群CW1；

从W1和CW1中选取M1个最优粒子组成新的种群NW1；

更新pi( t )和pg( t )；

end while

对于种群W2，在元胞空间中，每个子群

t=1；

while（t ＜Tmax）

利用式（10）计算w；

for i=1 to M1do

for j=1 to h do

if fitness( ci( t ))＜fitness( ci+q( t))更新ci( )

t ；

end if

end for

利用式（9）更新粒子的速度；

利用式（10）更新粒子的位置；

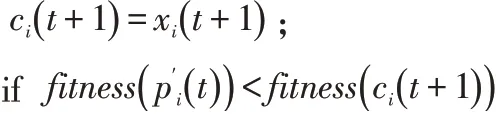
更新p′i( t )；

end if

更新p′g( t )；

end if

end for

利用式（19）和式（20）对当前种群进行变异，得到新的种群CW2；

从W2和CW2中选取M2个最优粒子组成新的种群NW2；

更新p′i( t )和p′g( t )；

t=t+1；

end while

从种群W1和W2中选取最优解作为全局最优解。

end

2.2 采用改进BP神经网络的交通流量预测

在BP 神经网络中，本文利用改进的PSO 算法选取最优的权值和阈值，使用改进后的BP 神经网络预测交通流量，具体的算法如下：

算法2 改进的BP 神经网络的交通流量预测

输入：输入层节点数A，隐含层节点数B，隐含层数，输出节点数Q，学习速率η，短时交通流量数据；

输出：短时交通流量预测结果；

begin

J=0；

将式（3）计算粒子的适应度，利用算法1 获取初始权值和阈值；

do

利用式（3）计算误差；

利用式（4）-（7）更新隐含层和输出层的权值和阈值；

J=J+1；

while（E ≤0.001 or J ≤500）

根据最优的权值和阈值建立基于BP 神经网络的交通流量预测模型；

利用建立的BP 神经网络预测交通流量；

end

3 实验与分析

3.1 实验数据与评价指标

实验数据来自OpenITS（http://www.openits.cn）提供的公开数据集，开放的数据是安徽省宣城市在2016 年12 月15 日全天的交通流量数据。

本文采用均方根误差（Root Mean Square Error，RMSE）和平均绝对误差（Mean Absolute Error，MAE）作为衡量交通流量预测结果的指标，RMSE 的公式为：

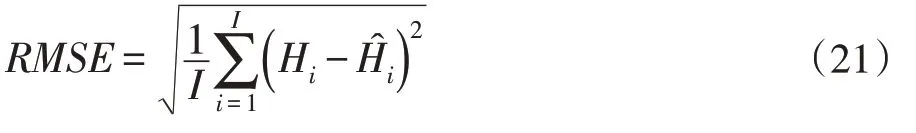
MAE 的公式为：

其中，I 为样本数，Hi为实际数据值，i为预测数据值。

3.2 实验参数

在实验中，改进的BP 神经网络涉及到的参数设置如 下：A=4 ，Q=3 ，η=0.01 ，vmax=4 ，wmax=0.9 ，vmin=0.1，Tmax=500，c1=c2=2，q=8。为避免隐含层节点数过多而出现“过拟合”问题，本文采用以下公式确定隐含层节点数[11-12]：

其中，输入层的节点数为A，隐含层的节点数为B，输出层的节点数为Q，a 是1 ～10 之间的常数，本文设置a=7。

3.3 结果与分析

为验证本文提出的BP 神经网络DPSO-BP 在交通流量预测中的有效性，将DPSO-BP 与BP 神经网络、IPSO-BP、CPSO-BP、GCS-BP、TCS-BP 进行比较。对全天每隔1 个小时的交通流量数据进行采样和预测，各改进的BP 神经网络对交通流量预测的比较如图4和表1 所示，从图3 和表1 可以看出，与现有的BP 神经网络相比，通过DPSO-BP 得到的交通流量预测结果最接近于真实的交通流量，而且DPSO-BP 的RMSE 和MAE 值最小，这说明采用DPSO-BP 得到的交通流量预测结果最稳定。

通过上述比较可以看出，本文提出的BP 神经网络DPSO-BP 在对交通流量的预测效果方面要优于现有的BP 神经网络，这是因为本文将改进的PSO 算法应用于优化BP 神经网络的初始权值和阈值，提出的改进PSO 算法分别在两个种群中采用了不同的寻优策略进行寻优，这样可以提高种群多样性和寻优能力。此外，在两个种群中都使用了差分进行算法对种群进行变异，并获得变异种群，这样可以帮助种群跳出局部极小值，扩大寻优范围。因此，改进的PSO 算法在寻优能力和收敛性方面要优于现有的PSO 算法和CS 算法，通过改进的PSO 算法得到的BP 神经网络的初始权值和阈值则更加有效。

图4 各算法的交通流量预测比较

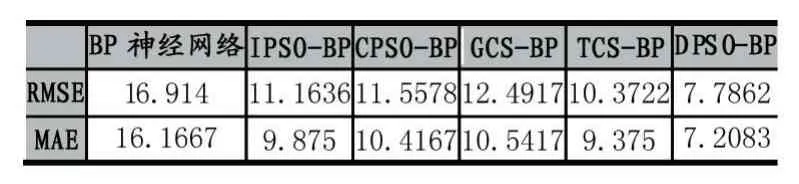
表1 各算法的RMSE 和MAE 比较

4 结语

权值和阈值的初始值影响BP 神经网络的寻优能力和收敛性。本文提出采用改进的PSO 算法提高BP神经网络的优化效果。在改进的PSO 算法中，本文采用双种群同时寻优的策略提高PSO 算法的全局寻优能力和收敛性。对交通流量的预测实验说明，与现有的BP 神经网络相比，本文采用基于改进PSO 算法的BP神经网络能够准确地预测交通流量，且具有较好的稳定性。