基于蚁群算法的高校排课问题的应用研究

蒋正锋，覃韩，吕佩佩，刘溯奇

（广西民族师范学院数学与计算机科学学院，崇左532200）

0 引言

20 世纪50 年代，一些国外学者首次研究了自动排课系统，如Gotlieb 在1963 年提出了自动排课的数学模型，并对排课问题进行深入的研究，而我国对自动排课的研究始于80 年代初期，起步是比较晚，但取得了一定的成果[1-3]。

自2016 年秋季以来，广西民族师范学院的课程安排任务从教务处下放到二级学院。一般是二级学院教学秘书手工安排课程，这将是非常耗时耗力，并且教学资源之间有可能存在冲突等情况，排课效果不尽人意。鉴于高等教育招生规模进一步扩大，入学大学生人数不断增加，相对有限的教学资源提高了课程安排任务的难度和复杂性，如何设计一个多约束高效的自动排课系统替换二级学院手工排课已成为目前亟待解决的问题[4]。考虑广西民族师范学院的具体情况，根据各种自动排课算法[5]的特点，本文探讨了使用蚁群算法来解决排课问题。

1 排课问题分析

1.1 排课问题五要素

如何合理配置有限的教学资源已成为每个高校避不开的问题，其中编排科学且合理的课表是这个问题的核心部分。排课问题需考虑课程、教师、班级、教室和时间五要素之间的相互制约的不确定因素，它是一多约束、多目标优化的时间表问题，使编排的课表尽可能满足全校师生的要求。排课过程中涉及到课程、授课教师、上课班级、教室和时间五要素[10]，将其定义为如下的集合：

（1）课程集合：CO={ CO1,CO2,CO3,…,COL }，其中L 是开设课程的数量。

（2）授课教师集合：TE={TE1,TE2,TE3,…,TEK}，其中K 是全校授课教师的数量。

（3）班级集合：CL={CL1,CL2,CL3,…,CLN}，其中N是全校班级的个数。

（4）教室集合：CR={CR1,CR2,CR3,…,CRP}，其中P是不同类型教室的总数。

（5）时间集合：TI={TI1,TI2,TI3,…,TIQ}，其中Q 为25，表示时间片的个数。

1.2 排课问题的约束条件

课表的五要素之间是相互制约的，尽可能的去满足约束条件，探索五要素之间最优的组合，排出比较合理的课表。排课过程中涉及到的分硬约束和软约束两类，其中硬约束是课表必须满足的约束条件，软约束是可选的约束条件，它起优化课表的作用。硬约束和软约束[2,5,9]如下所示：

●硬约束

（1）上课教室在相同时间内，只能排一门课程。

（2）上课班级在相同时间内，只能排一门课程。

（3）授课教师在相同时间内，只能排一门课程。

（3）授课教师在相同时间内，只能给一个班级授课，合班除外。

（4）授课教室容量大小必须大于或等于上课班级的人数。

（5）学校上课教室的总数量必须大于或等于同一时间内上课的总课程数。

（6）上课教室类型要与课程对教室要求的类型匹配。

●软约束

（1）同一班级的课程应均匀分散在一周内。

（2）同一教师同一门课程不同班级授课，同一天每个班级都安排授课内容，保证教学的连贯性。

（3）同一门班级同一门课间隔安排，至少间隔一天，但也不能超过两天。

（4）体育课一般安排在下午，并且体育课后不再安排其他课程。

（5）连续上课或授课时，教室之间的距离不能太远。

（6）数学类课程或专业课，安排在上午，选修课安装在晚上或者周末。

（7）教师的授课任务间隔安排均匀分散在一周内。

2 蚁群算法概述

2.1 蚁群算法的基本思想

蚁群算法是一种从自然界观察蚁群觅食行为中衍生出来的仿生优化算法，蚁群借助释放一种称为信息素（pheromone）的物质相互协作来发现巢穴与食物之间的最短路径。蚁群算法最初是用于解决TSP（Traveling Salesman Problem）问题，TSP 问题具有广泛的代表性，许多其他的问题都可抽象为类似TSP 问题来求解。

（1）蚁群算法的模型描述

一只蚂蚁要去m 个城市觅食，它先随机选择其中一个城市作为起点，然后再逐个到达其他所有的城市，蚂蚁在觅食过程中释放随时间推移而挥发的信息素，最后回到起点城市，要求蚂蚁每个城市只能达到一次，那么蚂蚁按什么顺序访问城市使得觅食的总行程是最短[6]？

（2）构建蚁群算法的数学模型[10]

假设求解问题的规模即觅食城市数为m，蚁群中蚂蚁的数量为n 只，则城市集合V={v1,v2,…,vm}，城市之间路径的集合E={（r,s）|r,s∈V}。定义ci(t)(i=1,…,m)为t 时刻位于城市i 的蚂蚁数量，故总的蚂蚁数量n 的计算如公式（1）所示。

蚁群算法中出现了禁忌列表、信息素和能见度等概念。禁忌列表是记录蚂蚁经过的城市，为了避免蚂蚁多次走进同一城市而设置的一种数据结构，Tubek为蚂蚁k 的禁忌表，蚂蚁k 经过城市i，则将城市i 添加到禁忌表Tubek，Tubek(q)是蚂蚁k 的禁忌表中第q 个元素，表示蚂蚁k 经过的第q 个城市。信息素是蚂蚁释放出来的一种物质，这种物质的浓度随时间推移而挥发。能见度也称为启发信息，定义为两城市间距离的倒数，如公式（2）所示。

σij( t )为城市i 与城市j 之间的启发信息，dij是两城市间的距离。城市间距离越近，启发信息就越大，引导蚂蚁搜索，路径被选择的概率就越大，这种启发信息是固定不变的。

Pijk(t)表示t 时刻时，蚂蚁k 从城市i 转移到城市j的概率，Pijk(t)的定义如下公式（3）所示。

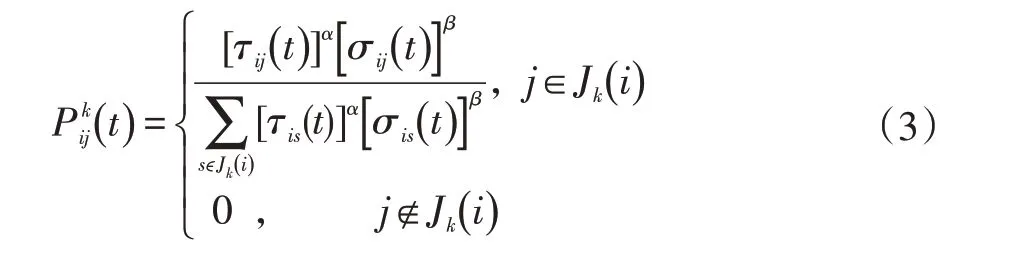
其中τij( t )为t 时刻两个城市间路径（i,j）上残留的信息素，α 是信息启发式因子，残留信息的重要程度，β 是期望启发式因子，是信息的相对重要程度。 Jk(i)表示蚂蚁k 在城市i 时，下一步允许转移到的城市集合，定义为如下公式（4）所示。

每只蚂蚁觅食访问完所有城市后，城市间路径的信息素浓度会发生改变，所以需要对路径上的信息素进行更新，信息素更新的计算如下公式（5）、（6）和（7）所示。

其中Δτij(t)为t 时刻路径（i,j）上增加的信息素，是t 时刻蚂蚁k 在路径（i,j）上增加的信息素。ρ 是信息素蒸发系数，1-ρ 为信息素的持久性系数。蚂蚁释放的信息素量为Q，Lk是蚂蚁k 是经过所有城市的总路径长度。

2.2 蚁群算法的二分图模型

二分图模型[10]是由顶点、边和权值三部分组成的无向图G=（N,S,C），图中所有顶点N 划分为互补的两个集合，不同集合顶点的连接构成了边集合S，边的权值集合C 是选择下一个顶点的依据。二分图模型如下图1 所示。

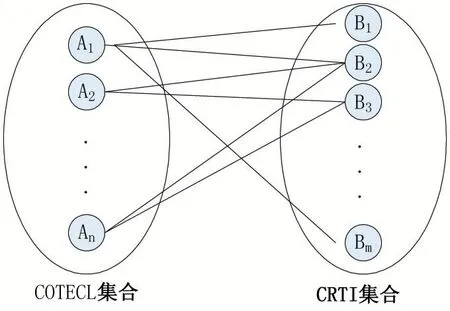
图1 二分图模型

排课问题的五要素课程、教师、班级、教室和时间的笛卡尔积CO×TE×CL×CR×TI 就构成排课问题的解空间，排课问题就是在这个解空间上寻找满足所有硬约束条件并且尽可能满足软约束条件的解。因为任课计划表中教师给哪个班教授什么课程是确定的，所以课程、教师、班级的笛卡儿积CO×TE×CL 简化为COTECL，教师和时间是满射的关系，其笛卡儿积为CRTI=CR×TI。

（1）二分图的顶点集合

开设哪些课程是根据培养方案先制定下学期合理的任课计划表，任课计划表中教师给哪个班教授什么课程是确定的，因此课程、教师和班级看成绑定在一起的组合，把排课问题中的课程、教师和班级组合组成的COTECL 集合作为二分图左边的顶点集。教室和时间动态组合组成的CRTI 集合作为二分图右边的顶点集。

（2）二分图边的集合

二分图左边COTECL 集合中的顶点与右边CRTI集合中的顶点只要满足对教室安排的两个基本条件才能进行连接构成边的集合。对教室安排要满足的两个基本条件：一是COTECL 集合顶点中班级的人数要少于CRTI 集合顶点中教室的容量，二是COTECL 集合顶点中课程对教室要求的类型与教室的类型是一致的。

（3）二分图边的权值

二分图中边的权值是根据具体课程时间的期望度来设置，排课过程中通过依据合理的权值才能排出高质量的课表。

3 基于蚁群算法的自动排课模型

蚁群算法解决排课问题[7,9]，需建立特殊的图形结构，由排课问题分析可知，排课过程中的课程、教师、班级、教室和时间五要素之间的关系转成COTECL“课程、教师、班级”和CRTI“教室、时间”之间的关系，则使用二分图模型可解决两个互不相交COTECL 集合和CRTI 集合的最大匹配问题。

构造排课问题满足硬约束条件的二分图模型，可完成排课问题的基本需求，即任课计划中应开设的班级课程都在右边顶点集中，教室要满足安排所有课程的需求，以及教师、班级、课程时间不冲突，但是优化课表，还需要使用蚁群算法进一步的动态调整[5]。

3.1 蚁群算法排课步骤

步骤1：参考任课计划表，把排课问题的五要素分成两个顶点集合COTECL 和CRTI，然后连接满足条件的COTECL 和CRTI 集合中的顶点，构建边集合及边两边顶点公用权值信息表，建立二分图模型。

步骤2：初始化蚁群算法中信息启发因子、期望启发因子、信息素蒸发系数、循环迭代次数、信息素浓度记录表等参数。

步骤3：初始化所有教师时间分配表、班级时间分配表和教室时间分配表，初始化每只蚂蚁的临时课表、个体权值、禁忌表、访问过的顶点集和CRTI 中教室和时间的分配表。

步骤4：判断迭代优化是否结束，如果CNT＜=MAXITER 为假，则跳转到步骤11。

步骤5：所有蚂蚁分别随机分配COTECL 集合中的一个顶点，初始化每只蚂蚁的个体权值和课表。

步骤6：判断每只蚂蚁是否访问过所有COTECL集合中的顶点，如果访问了所有的顶点，则跳转到步骤10，否则随机选择一个没有访问过的顶点。

步骤7：计算每只蚂蚁的转移概率Pij( t )，然后使用轮盘赌算法去选择路径。

步骤8：判断是否满足硬约束，如存在冲突，则跳转到步骤7 重新选择路径。

步骤9：记录选好的路径，修改蚂蚁个体课表、禁忌表、访问过的顶点集和个体权值，跳转到步骤6。

步骤10：更新二分图模型的信息素浓度值，跳转到步骤3。

步骤11：输出个体权值即代价最小的课程表。

3.2 蚁群算法自动排课流程图

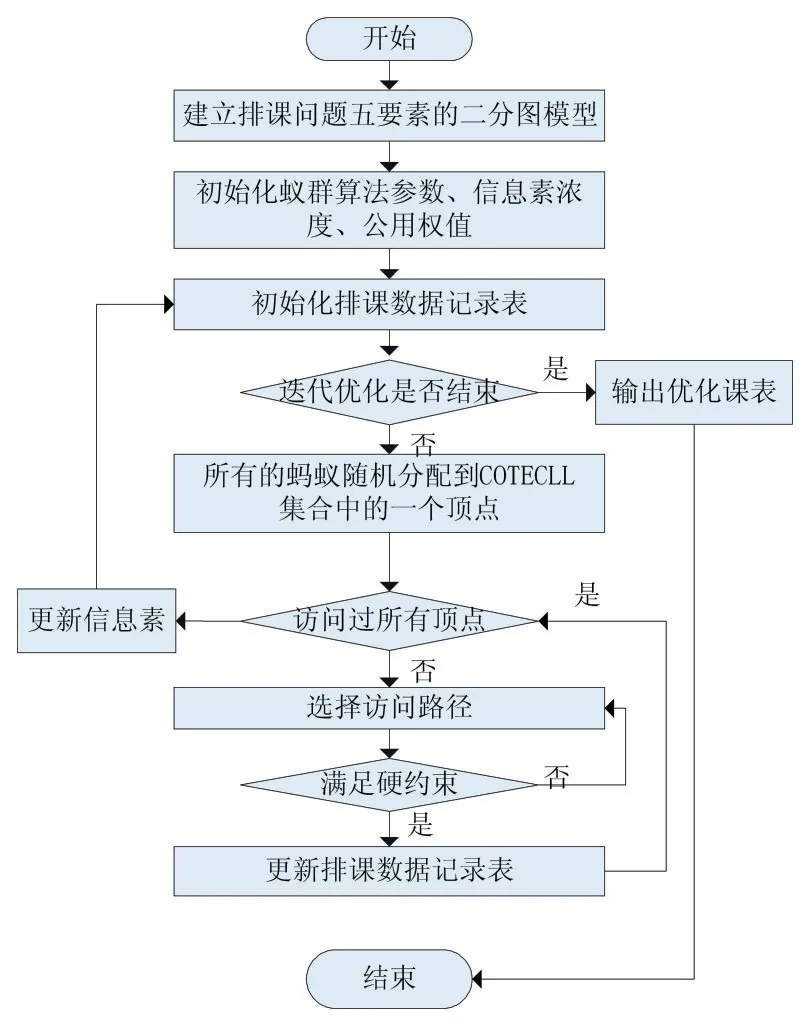
图2 蚁群算法自动排课流程图

4 基于蚁群算法智能排课系统

本排课系统采用B/S 结构，前端使用HTML、CSS、JavaScript 和Bootstrap 等技术，后端采用SSM 框架技术，最后通过自动化构建工具Maven 来管理整合整个项目。

排课系统面向的学校管理人员、教师和学生，所以根据使用系统用户对象的不同，整个系统分管理员操作模块、教师操作模块和学生操作模块，用户登录界面如图3 所示。

图3 基于蚁群算法智能排课系统的登录界面

自动排课是属于管理员操作模块，也是本系统最为核心的部分。管理员成功登录后，进入管理员操作界面，主要有班级管理、课程管理、教师管理、教室管理和自动排课等功能模块，系统功能界面如图4 所示。

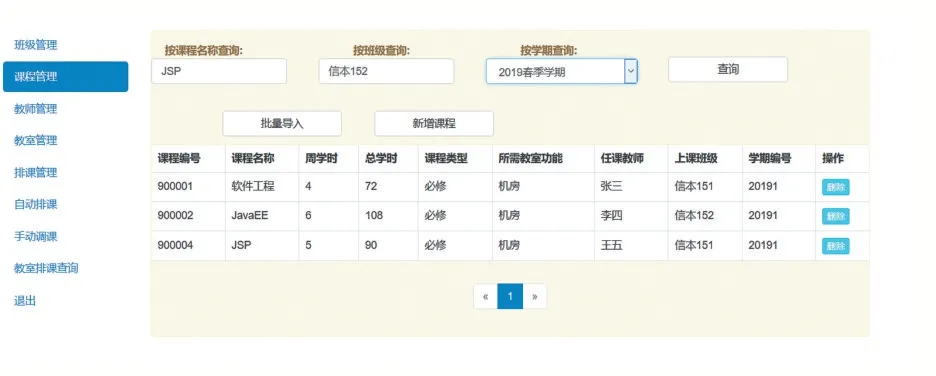
图4 基于蚁群算法智能排课系统功能界面

其中自动排课是经过班级、课程、教师和教室等基本数据维护后进行自动排课，可对生成的课表进行查看、修改、检查和确认操作。确认自动排课课表之前可进行课表检查及手动修改，最终确认后，将课表数据维护到系统数据库中，系统自动排课界面如图5 所示。

自动排课保存到数据库中的课表是班级课表，课表分班级课表、教师课表和教室课表三种，但教师课表和教室课表可由班级课表变换得到。某教师登录排课系统查看自己下学期授课任务的课表如图6 所示。

图5 基于蚁群算法智能排课系统自动排课界面

图6 教师查看自己的课表

5 结语

如何合理配置有限的教学资源已成为每个高校避不开的问题，其中编排全校科学与合理的课程表是这个问题的核心部分。本文简单介绍了蚁群算法及二分图的基本原理，并对排课问题的硬约束和软约束条件进行了分析，考虑广西民族师范学院的具体情况，对蚁群算法以及二分图匹配策略进行分析，设计了一个基于蚁群算法的自动优化课表的排课模型，排课结果表明该智能排课模型先生成一个满足硬约束的基本课表，然后自动优化成较科学与合理的课表，省时又省力。随着学校的快速发展及招生规模的进一步扩大，以及学校教务管理工作的变化，因此排课问题有待于进一步研究。