基于指数趋近律滑模控制DC-DC 变换器控制研究
2019-10-19张鹏翔陈国初俞庆
张鹏翔,陈国初,俞庆
(1.上海电机学院,上海201306;2.上海电气风电设备有限公司,上海200241)
0 引言
DC-DC Boost 变换器在新能源发电、电动汽车等领域有十分广泛的应用。由于DC-DC Boost 变换器具有特殊时变非线性的特点,控制器的设计具有较高难度。传统线性的双闭环PI 控制能够满足设计工作点周围的稳定要求,但不能保证变换器偏离设计工作点的稳定性。滑模控制器是一种针对变结构系统为控制对象的非线性控制,与线性的双闭环PI 控制器相比,滑模控制器对输出负载的变化具有较好的鲁棒性。滑模控制器负载变化与输入电压变化时拥有较好的鲁棒性和响应速度。近年来,滑模变结构控制在DC-DC 变换器的应用研究成为了热点。文献[1]中提出了一种基于输出电压的PID 控制滑模变结构控制,这种方法设计简单易于实现,但仅考虑了输出电压的影响,没有考虑电流的影响。文献[2]采用了Super-Twisting 高阶滑模控制算法来控制Buck-Boost 变换器,通过将不连续控制量作用在其高阶导数上,降低了一阶滑模面的抖振,但设计较为复杂。文献[6]以输出电压为控制量设计了Buck 变换器的模糊滑模控制,并进行了自适应控制的改进。
本文分析了Boost 电路连续导电模式的工作工程,得到其状态空间模型。并基于此模型进行滑模控制的设计,分析滑模控制的存在性与稳定性,最后设计仿真实验控制进行验证。
1 Boost电路建模
Boost 变换器是一种常用的直流升压变换器,具有典型的非线性特征。Boost 变换器在开关管导通与关断的工作状态如图1 和图2 所示。在充电过程中,开关闭合,开关处用导线代替。此时,输入电压流过电感。二极管防止电容对地放电。输入为直流电,电感上的电流以一定的比率线性增加,上升比率与电感大小有关。随着电感电流增加,电感开始储能。放电过程中,当开关断开时,由于电感的电流保持特性,流经电感的电流不会马上变为0,而是缓慢的由充电完毕时的值变为0。而原来的电路已断开,于是电感只能通过新电路放电,即电感开始给电容充电,电容两端电压升高。

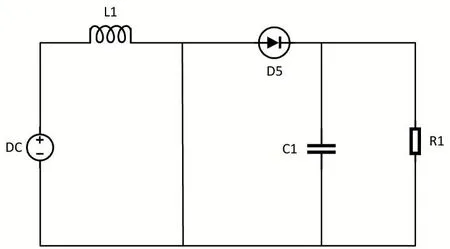
图1 开关管导通状态
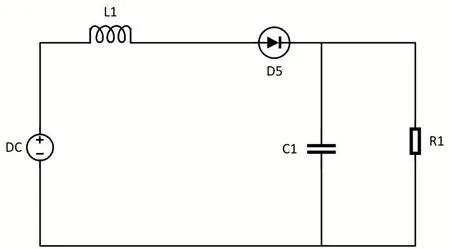
图2 开关管关断状态

则Boost 变换器在一个完整周期内的状态空间方程为:
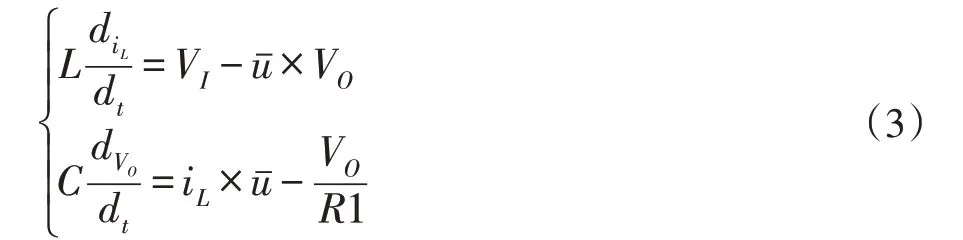
其中,VI为输入电压,VO为输出电压,iL为电感电流,iR为电阻电流,L 为电感值,C 为电容值,u 为开关器件的开关状态(开关开通u=1,开关关断u=0)。
2 滑模变结构控制器设计
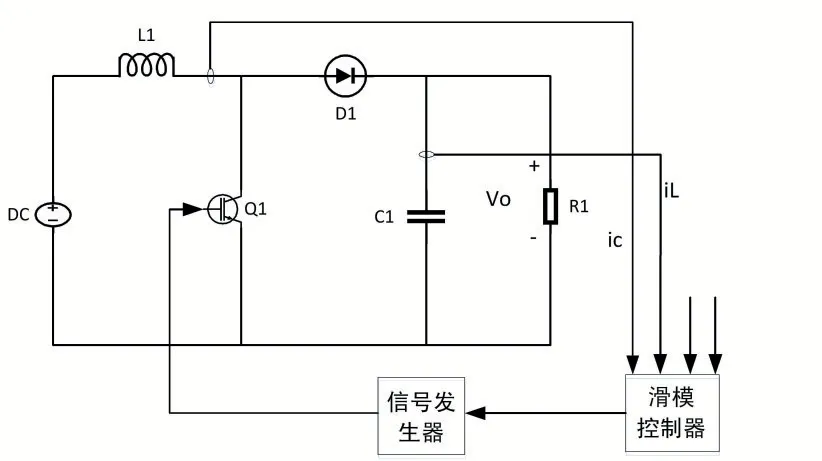
图3 滑模控制调制形式

控制状态变量选择电压误差x1,电流误差x2以及电流与电压的误差积分,表达式为:

其 中 Vref为 输 出 电 压 的 参 考 值 ,为电感电流的瞬时参考值,k1、k2分别为电压误差与电流误差的比例值。设计以3 个状态变量组成的滑模面:S=a1x1+a2x2+a3x3,a1、a2、a3为滑模面的滑模系数。
将Boost 变换器的状态空间方程式(3)代入式(5)并对时间进行微分可得到电路的动态模型:
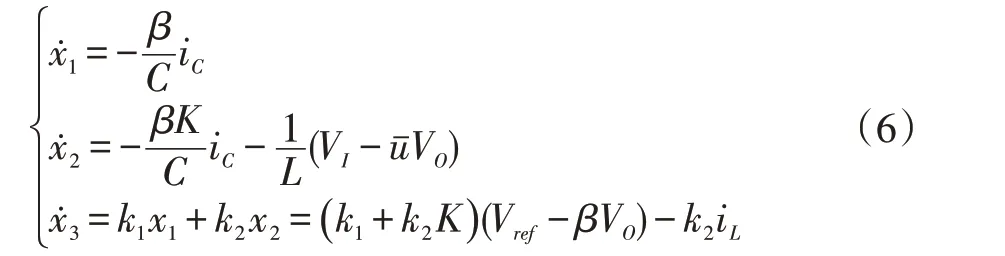
其中ū=1-u,滑模运动包含趋近运动和滑模运动两个过程,趋近运动即系统从任意状态向切换面的过程,由于开关器件的开关频率有限、延时及状态轨迹在趋近滑模面惯性的影响。为对趋近运行的运行轨迹进行改善使其快速运动到滑模面,可以引进趋近律对变换器趋近运动的动态品质进行改善,本文采用指数趋近律=-ε sgn s-ηs,减少状态运动到切换面的趋近时间。将式(6)代入求解得到等效控制:
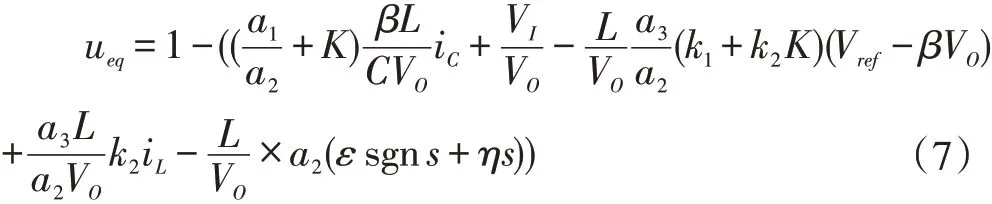
ueq为连续值,且在范围0 和1 之间。同乘VO可得:
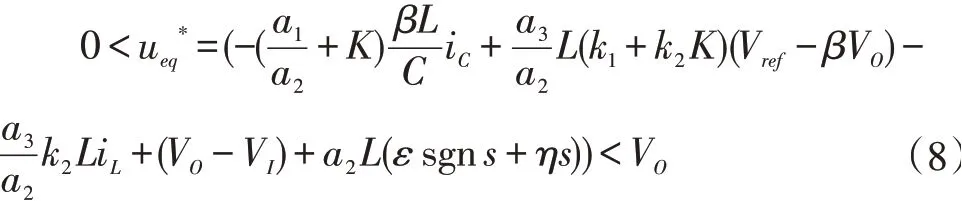
令 占 空 比 d 设 置 为 d=ueq,并 设 置,设计控制信号Vc与斜坡信号Vramp,但由于所设计方程采用的参数数值较大,不太适合直接在电路中使用,尤其在电压等级较高的场合。因此引入比例因子g,则方程为:
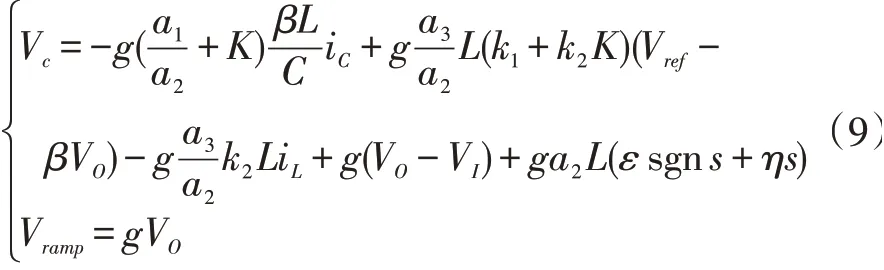
3 滑模控制分析
3.1 可达性分析
可达性即为变换器状在趋近运动过程后达到滑模面,且运动轨迹能保持在滑模面周围较小区域内的能力,为保证可达性的要求需要满足
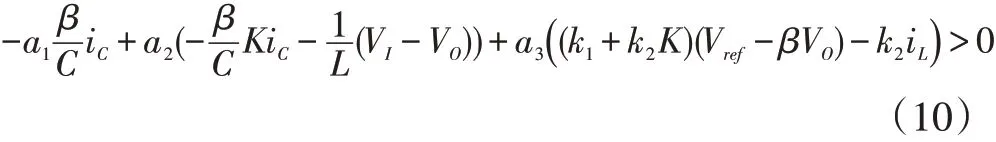
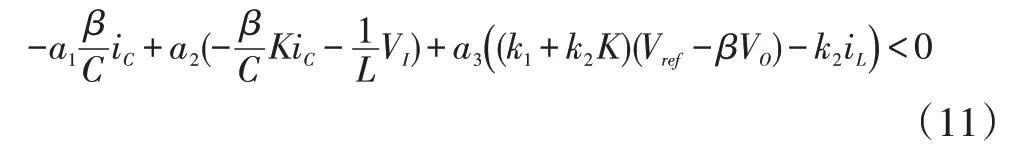
可化简为:
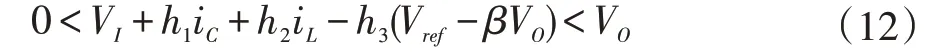
若变换器的工作最大值与最小值满足存在性条件,则可以表明变换器的全部工作范围都能满足存在性的要求。采用输出的预期稳态值替代VO,可以保证变换器的工作状态在原点周围区域内满足存在性要求,可得存在条件为:
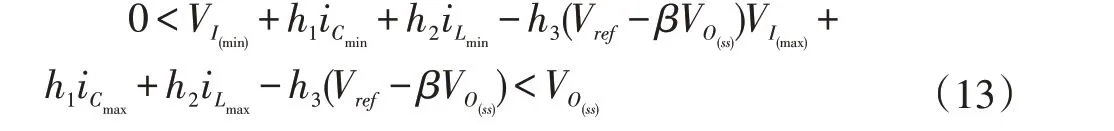
3.2 稳定性分析
Boost 电路的滑模控制器的运动方程是由电压和电流的状态变量组成,非线性程度较高且有较高的求解难度,为降低求解难度采用等效控制进行分析。将ueq带入变换器的状态空间方程中可得:
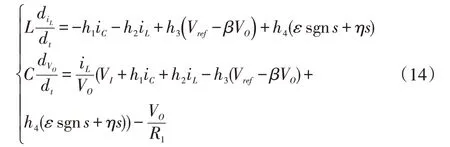
假设滑模面上存在平衡稳定点,且理想滑模状态最终停留在此点,平衡点满足
则状态空间方程可以化简为:
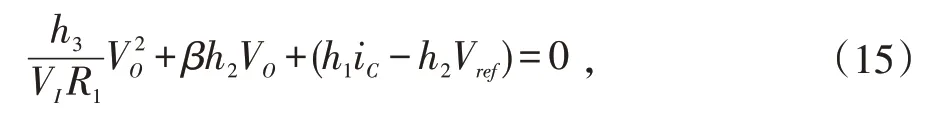
求解此方程可得:
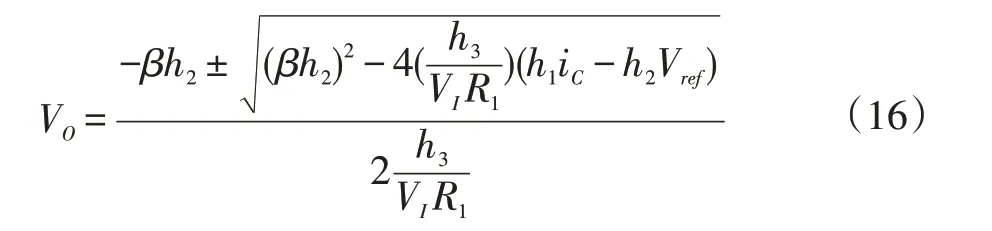
此方程的正实数解为输出电压的平衡点,则系统稳定的约束条件为:
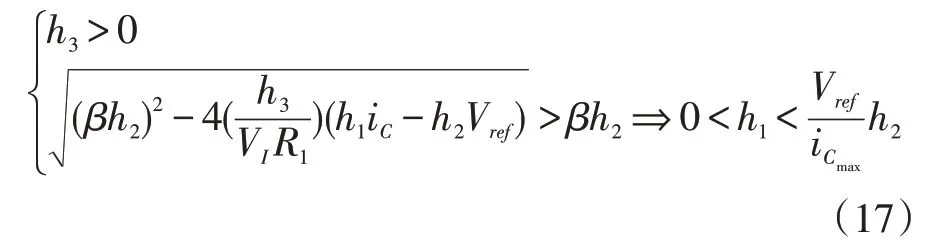
4 仿真与实验验证
为了验证所设计Boost 滑模控制器的有效性与可行性,在MATLAB/Simulink 中搭建Boost 电路的仿真模型,Boost 变换器电路参数如表1 所示。

表1 Boost 变换器参数
分别采用本文所设计滑模控制与传统PI 控制对Boost 变换器进行控制,观察变换器在加载启动、负载突加突减、输入电压变化突变的情况下,两种控制的控制效果。
图4 显示了Boost 变换器在滑模控制及PI 控制下的100Ω 负载加载启动输出电压的波形,滑模控制在0.01s 达到了稳定状态,PI 控制在0.06s 达到稳定状态,与PI 控制相比滑模控制拥有较短的稳态时间与超调量。图5 为负载突减的输出电压波形,在t=0.2s 时,负载由100Ω 切换到50Ω,图6 为电压突变的输出电压波形,在t=0.2s 时,输入电压由500V 突变为600V 。通过输出电压的仿真波形上可以得出,利用本文设计的滑模控制策略控制Boost 变换器,在负载加载启动、负载突增突减及输出电压波动时,输出电压的波动范围均停留在稳态值较小的范围内。而常规PID 控制器在变换器存在较大扰动影响时,出现较大的负调现象,具有较长的过渡时间,动态品质不够理想。
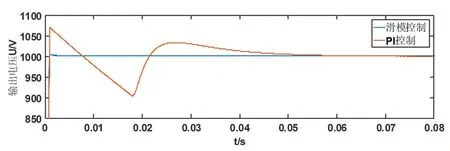
图4 滑模控制与PI控制负载加载启动输出电压波形
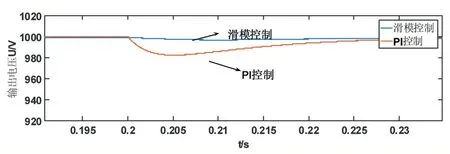
图5 滑模控制与PI控制在负载突减输出电压波形
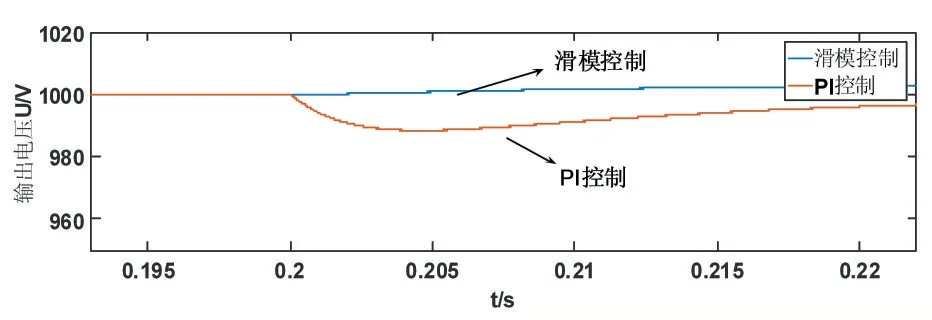
图6 滑模控制与PI控制在电压变化输出电压波形
5 结语
本文首先根据Boost 变换器在连续导电工作模式下的运行状况得到其状态空间模型,然后设计了以电压误差、电流误差及电流电压误差积分和为状态量的滑动模态面,为改善趋近运动的运动轨迹引入指数趋近律改善其趋近运动的动态性能;随后,通过理论分析推导得到其的存在与稳定条件,最后通过仿真实验对比滑模控制与PI 控制在负载突加突减及输入电压变化下的控制效果,可以得出本文采用的滑模控制相较PI 控制对系统参数变化有具有较小的过渡时间,较好的动态品质,较高的鲁棒性。
