基于深度学习的MPSK信号调制识别*
2019-10-14刘明骞郑诗斐李兵兵
刘明骞,郑诗斐,李兵兵
(1. 西安电子科技大学 综合业务网理论及关键技术国家重点实验室, 陕西 西安 710071;2. 西安电子科技大学 信息感知技术协同创新中心, 陕西 西安 710071)
信号的调制识别是通信侦察、认知无线电等领域的关键技术,它在复杂环境和干扰噪声的情况下,不需要其他的先验知识,就能判断信号的调制方式,并提取相应的调制参数,为信号的进一步分析处理提供依据[1]。按调制识别依据理论的不同,可以分为依赖先验知识的判决论方法以及基于特征提取和分类器设计的统计模式识别方法。国内外众多学者在这方面做了大量的研究,各种调制识别方法也不断涌现。其中,一些学者利用循环谱对数字调制信号进行识别[2]。但是,在这些识别方法中,针对多进制相移键控(Multiple Phase Shift Keying,MPSK)信号的识别效果不理想,本文针对这一问题开展了进一步的研究。
近年来,深度学习在模式识别等领域取得了突破性的进展,也有部分学者将其应用于通信信号的调制识别。文献[3]提出了一种利用信号循环谱特征和深度自动编码器进行通信信号自动识别的方法。文献[4]采用两个深度自动编码器和通信信号的循环谱特征和小波特征进行了调制识别,当信噪比为10 dB时,识别率可达到95%。但是,在低信噪比环境下,识别性能欠佳。
本文从人工智能角度出发,解决基于循环谱的高阶MPSK(M≥4)信号识别困难的问题,提出基于深度学习的MPSK信号识别方法。
1 基于循环谱的特征参数
1.1 信号的循环谱
信号x(t)是广义循环平稳过程,自相关函数为
Rx(t;τ)=E{x(t)x*(t-τ)}
(1)
式中,τ为时间间隔。根据周期性可将Rx(t;τ)展开为Fourier级数的形式[5]。
(2)

(3)
其中,T为信号的持续时间。 如果x(t)是各态历经过程,则
(4)
循环自相关函数的傅立叶变换被称为循环谱密度函数,简称循环谱[6],其表达式为
(5)
式中,f为信号频率。α≠0时,平稳噪声的谱相关函数等于0,因此循环谱具有抗噪声性能。
二进制相移键控(Binary Phase Shift Keying, BPSK)信号可表示为
(6)

则BPSK信号的循环谱为
(7)

MPSK(M≥4)信号可表示为
(8)
式中,φk为被调相位,有M种不同的取值。
则MPSK(M≥4)的循环谱为
(9)
1.2 循环谱的等高图
目前,国内外针对信号循环谱的估计算法进行了诸多研究,其中,应用较为广泛的有时域平滑算法中的快速傅立叶变换累加算法(fast Fourier transform Accumulation Method,FAM)[7]和分段谱相关函数算法(Strip Spectral Correlation Algorithm,SSCA)以及频域平滑算法(Frequency Smoothed Method,FSM)。为了减少计算量,本文采用时域平滑算法估计MPSK信号的循环谱。
循环谱时域平滑算法估计表达式为

g(n-r)
(10)
式中,XT(r,f)被称为复解调,表示信号x(n)加窗后的短时傅立叶变换,其计算公式为
(11)
其中:a(n)为数据衰减窗;g(n)为平滑窗;Δt为数据采集时间,Δt=NTs,N为样本数,Ts为采样周期,N′为傅立叶变换的长度,T为复解调所需N′点离散傅立叶变换(Discrete Fourier Transform, DFT)数据时间。式(10)计算的是循环谱中点(α0,f0)处的幅度值。
选取常用的MPSK信号中BPSK、正交相移键控(Quadrature Phase Shift Keying, QPSK)和八进制相移键控(8 Phase Shift Keying, 8PSK)为例,图1给出MPSK信号的循环谱的等高图。从图1中可以直观地看出,不同调制的MPSK信号,它们的循环谱等高图是不相同的。因此,将MPSK信号循环谱的等高图作为特征参数用于调制识别。
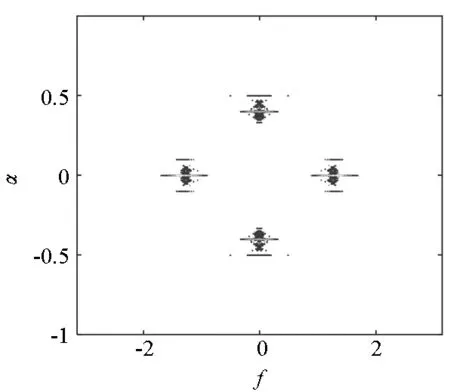
(a) BPSK的循环谱等高图(a) Cyclic spectrum contour maps of BPSK

(b) QPSK的循环谱等高图(b) Cyclic spectrum contour maps of QPSK

(c) 8PSK的循环谱等高图(c) Cyclic spectrum contour maps of 8PSK图1 MPSK的循环谱等高图Fig.1 Cyclic spectrum contour maps of MPSK
2 基于卷积神经网络的调制识别
2.1 卷积神经网络
标准卷积神经网络(Convolution Neural Network, CNN)[8]是一种特殊的前馈神经网络模型,一般具有比较深的结构,由输入层、卷积层、下采样层、全连接层、输出层组成。图2为标准卷积神经网络的整体结构。

图2 卷积神经网络结构模型Fig.2 Structure of convolution neural network
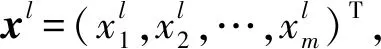
(12)

下采样阶段,运用平均池化方法[9]对每个特征图进行操作。下采样层的形式如式(13)所示。
(13)
式中,down(·)表示下采样函数,权值β一般取值为1,偏置bj一般取值为零矩阵,f(·)一般取为恒等线性函数f(x)=x。
在对网络进行训练时,通常使用反向传播法则和有监督训练方式[9]。神经网络中输入特征通过前向传播得到输出特征,假设输入为X,经过多层网络传播后得到输出特征图O。然后将得到的输出特征图O与给输入图像所加的标签G进行比对,根据一定的运算公式得到误差E。根据反向传播路径,将误差E层层传播,并通过权值更新公式对卷积层的权值wi,j进行调整。随着迭代次数的不断增加,网络误差逐渐降低,并最终收敛到稳定的权值集合。在训练过程中,网络中权值的初始化通常随机,而偏置的初始化往往全置为零。
反向传播过程中优化的目标函数为
(14)
当L层是网络的最后一层时,输出层误差为
(15)
式中:σ(x)是一个向量值函数,在非线性情况下通常取为逐元sigmoid函数,或者逐元tanh函数,σ′(x)为其导数;“∘”代表两个向量的哈达马积。
当L层为卷积层时,
(16)
通过求和来计算偏差的梯度。
(17)
计算对权值的偏导数。
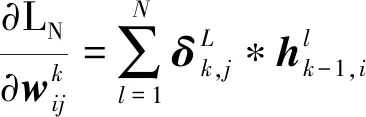
(18)
当L为下采样层时,
(19)
式中,rot180(·)表示把一个矩阵水平翻转一次再垂直翻转一次。
误差计算出来后,便可以用式(20)~(21)更新所有的网络参数。
(20)
(21)
2.2 调制识别方法的步骤
综上所述,所提基于深度学习的MPSK信号调制识别方法的具体步骤如下。
步骤1:利用时域平滑算法估计接收到的MPSK信号的循环谱,并提取信号循环谱的等高图转换为二维图像信息。
步骤2:对二维图像进行预处理,同时为了减少运算量,提取大小为81×81的像素块,并按照分类器所需的格式进行处理。
步骤3:确定卷积神经网络分类器的网络参数,并利用数据样本进行训练。
步骤4:在完成卷积神经网络的训练后,输入测试样本进行MPSK信号的调制方式识别。
3 仿真结果及分析
为了验证所提方法的有效行,基于MATLAB软件平台进行仿真实验。仿真实验的参数设置为:待识别的信号为BPSK、QPSK、8PSK,载波频率为4 kHz,码元速率为2 kBd,采样频率为20 kHz,各个信噪比下产生的每种信号的训练样本和测试样本分别为5000个和1000个,卷积神经网络的参数见表1。
在信噪比范围为0~10 dB的条件下,对BPSK、QPSK、8PSK信号进行调制识别。其中,训练样本的信噪比分别为0 dB、5 dB、10 dB,从而得到0 dB、5 dB、10 dB的测试样本的正确识别率见表2。从表2可以看出,在不同的信噪比下,该方法具有较好的识别结果,当测试样本信噪比为0 dB、5 dB、10 dB时,单个信号的正确识别率可达85%以上,信号的平均识别率高于90%。由此可见,所提基于深度学习的MPSK信号识别方法在不同的信噪比下具有良好的识别性能。
表1卷积神经网络中的参数设置
Tab.1 Parameter settings of convolution neural network

名称释义缺省值outputmaps输出映射面的个数6或12kernelsize卷积核的边的长度6或7scale滑动窗口的边的长度2opts.alpha学习率0.1opts.batchsize迷你块包含的样本数50opts.numepochs迭代次数50

表2 单信噪比信号训练样本的识别结果
为了提高训练样本集的完备性,将0 dB、5 dB、10 dB三种不同信噪比的信号同时进行训练,即构建这三种混合信噪比下MPSK(M=2,4,8)信号的训练样本集合。对信噪比为0 dB、5 dB和10 dB三种情况下单个信号的测试样本分别进行识别,其识别结果见表3。从表3可以看出,该方法在低信噪比下能够对MPSK(M=2,4,8)信号进行有效的识别。另外,在混合信噪比信号训练样本下信号的正确识别率高于单信噪比信号训练样本下的正确识别率。从而可以看出,训练样本数量的增多能够有效地提高信号的识别性能。
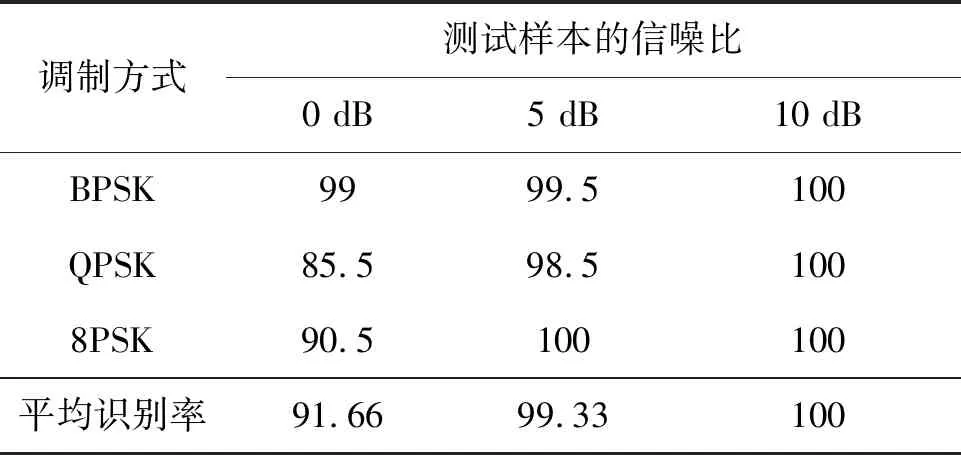
表3 混合信噪比信号训练样本的识别结果
在相同的仿真实验环境和相同的码元速率、载波频率、采样频率、采样点数等信号参数的设置下,信噪比分别在0 dB、5 dB和10 dB情况下,本文方法与文献[10]基于高阶累积量的方法和文献[11]基于循环谱的方法进行对比实验,对比结果见表4。从表4可以看出,在信噪比为0 dB和5 dB时,本文方法的平均识别率较文献[10]方法有了明显的提高;在信噪比为5 dB和10 dB时,本文方法的平均识别率比文献[11]方法高。并且在信噪比为0 dB、5 dB和10 dB的情况下,对于BPSK信号,本文方法的识别率优于文献[11]方法。本文方法的计算复杂度为O(N2log2N),文献[10]方法的计算复杂度为O(N),文献[11]方法的计算复杂度为O(N3log2N)。由此可以看出,本文方法的计算复杂度高于文献[10]方法,但在低信噪比条件下,本文方法的平均识别效果优于文献[10]方法;本文方法的计算复杂度低于文献[11]方法,并且本文方法能够解决文献[11]方法不能识别8PSK信号的问题。
该实验使用了带有两个Intel 酷睿i3 3110M CPU的PC,并且神经网络的运行效率良好。每个信噪比下每种信号的训练样本数为5000个,离线训练时间为20 539.87 s;每个信噪比下产生的每种信号的测试样本数为1000个,在线测试时间为165.247 591 s。相比而言,文献[10]方法中每种信号的测试样本数为1000个,每个信噪比下每种信号识别时间为0.764 339 6 s;文献[11]方法中每种信号的测试样本数为1000个,每个信噪比下每种信号识别时间为170.611 929 s。可见,所提方法的在线时间复杂度低于文献[11]方法,而高于文献[10]方法。
4 结论
本文提出了一种基于深度学习的MPSK信号调制识别方法。仿真结果表明,在不同的信噪比下所提方法具有良好的识别性能,并且针对高阶MPSK信号,所提方法比现有的基于循环谱的识别方法的识别性能更优。
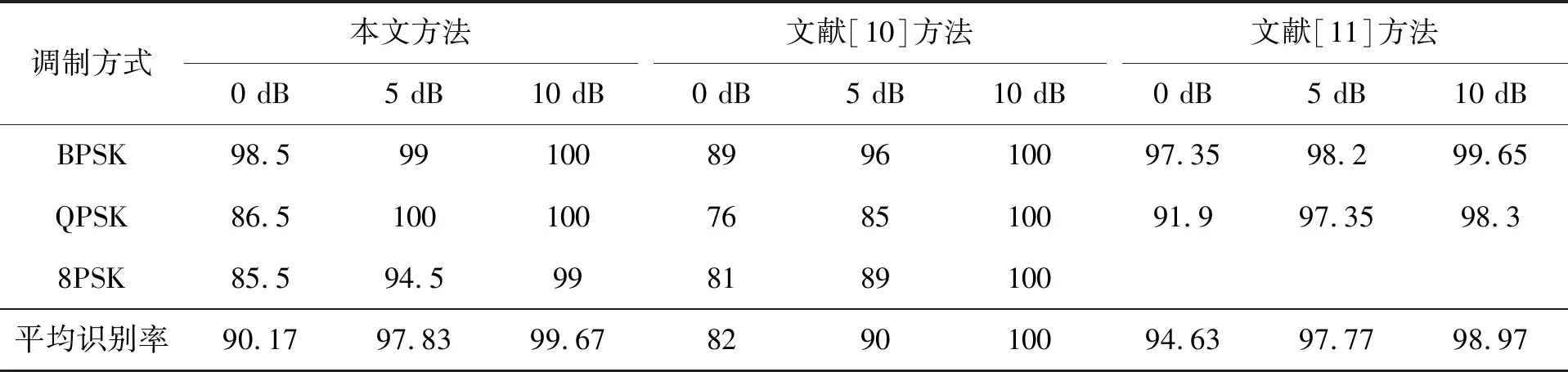
表4 三种不同方法的识别率对比
