高中数学立体几何几种高效解题方法探究

山东省寿光现代中学 李佳庆

在高中数学中，立体几何知识属于重点内容，也是学习的难点。因此，作为未来社会建设型人才，学生必须熟练掌握各种立体几何解题方法与技巧，并通过大量训练提高自身的解题质量与效率，从而促进自身更好地发展。

一、提高空间想象力

对高中数学学习而言，平面图形认识到立体图形认知实际上是一个飞跃，而这一飞跃需要较长过程。为了实现飞跃，一些高中同学会采取有效结合自制空间模型和数学题目的方式，并进行反复观察；另一些高中同学则会仔细观察并揣摩教材中的立体图形，对立体几何中线、角、面间的关系进行判断，找出辅助线作法，从而确立立体空间观念。这也就意味着在具体学习过程中，应该在综合考虑自身实际情况的基础上，合理选择解题方法，并逐渐建立空间观念，促进自身空间想象能力的提升，为后续立体几何问题的解决奠定基础。

在实际操作中，要想加强自身的空间感，应该采取简单模型构建的方式来激发自身的联想与想象。例如，可以先制作简单的长方体与正方体，之后通过仔细观察，明确其中线线、面面以及线面间关系，然后通过具体立体几何问题完成拓展延伸，以此来促进自身解决问题能力的提升。同时，在了解了空间几何线面关系后，高中生要想掌握高效、正确的解题方法，还应该培养自身的绘图能力。这就意味着高中生应该从简单绘图入手，并在掌握基本技法的基础上进行延伸，保证自身能够以题干为依据绘制图像，为想象与问题解决提供便利。

二、实现图形转换

图形转换也是有效解决立体几何题目的有效方式。在解答一些立体几何题目时，如求取值范围、求最值等，若可以灵活变化图形，并加强对运动变化理念的运用，那么就可以进一步分析问题，并快速解出正确答案。同时，高中生还可以通过构建辅助图形的方式，实现原命题特殊化，降低复杂问题难度，并将不熟悉的问题转化成常见问题。

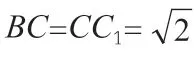
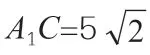
由此看来，在解答立体几何中范围和最小值问题时，要正确、合理地转变图形，并以变化观念分析、解决问题，只有这样，才能获得良好的解题效果，促进自身数学素养与学习能力的提升。

三、提高逻辑论证能力

在对高中数学立体几何知识进行学习时，还可以通过多种方式的运用，如类比平面几何、构建模型以及联系实际生活等，提出相应的命题或猜想。需要注意的是，在命题提出后，不能急于做出肯定或否定判断，而是要利用特例检验命题，并在对命题性质进行确定后，探索相应证明方法。在实际分析过程中，要想实现由局部到整体、由低到高，就必须在具体解题过程中融入逻辑论证能力与综合分析能力，这样不但可以提高解题效率与正确性，还能够锻炼逻辑论证能力与综合分析能力。同时还应该从不同角度分析立体几何题目，如综合处理距离、垂直、角以及平行等问题，只有这样，才能促进高中生解题能力的提升，并增强其数学素养。

四、综合运用解题技巧

在实际学习过程中，不能局限于自身思维，在对立体几何问题进行解决时，不但要运用立体几何知识，还应该综合运用各种解题技巧与知识体系。这也就意味着高中生应该在解题过程中综合运用运动距离、空间几何以及函数等思想，并通过对各种学习技巧的利用，找出最简的解题方法。

以线段最短问题为例：正方体ABCD—A1B1C1D1的棱长是3，其中棱AA1上有一点E，已知A1E为1，且是A1BD这一截面上不断移动点F，求AF与FE的最小值。

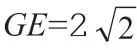
由此看来，在实际学习中，只有对思维进行发散，综合运用各种解题技巧，才能为解决立体几何问题提供便利，并促进自身学习效率的提高。

综上所述，掌握立体几何解题方法具有重要意义，熟练掌握立体几何相关知识，并通过提高空间想象力、实现图形转换、提高逻辑论证能力以及综合运用解题技巧等方式，提高解题的质量与效率，从而为后续学习奠定良好基础。