数形结合在初中数学教学中的应用

江苏省昆山市石牌中学 王维娟

数学不仅需要研究数量关系，还要研究图形，二者存在着对立和统一的关系，宇宙万物无不是数和形的矛盾统一。对此，国内外有很多专家对于数形结合都有着深刻的见解。我国著名数学家华罗庚说过：“数缺形时少直观，形少数时难入微，数形结合百般好，隔裂分家万事休。”数学中的很多概念、法则、公式、定理都与一定的空间形式密切联系。数形结合是具体和抽象的结合，是形象思维和抽象思维转化的桥梁，是逻辑含义和空间表达形式的展现。在拉格朗日的《数学概要》中描述：“只要代数同几何分道扬镳，它们的进展就是缓慢的，应用就狭窄，但当这两门学科结成伴侣后，它们就互相汲取新鲜的活力，从此便以快速的步伐走向完善。”

初中阶段正是学生打基础的阶段，教师应该重视数形结合的思想，通过多种方法不断渗透到教学中。基于此，本文立足于初中数学教学，结合本人教学时的体会，对数形结合方法和思想进行相关的探讨。

我们所接触到的初中数学中，数形结合在不等式、数列、最值问题、函数和解析几何等多方面都有涉及。

一、数形结合在不等式中的应用

例1：求不等式 |x+2|+|x-3| ＞5 的解集。

分析：这是一个绝对值不等式问题，既涉及了绝对值的知识点，还涉及了不等式里的知识点。

记数轴上表示数-2 的为点A，表示数3 的点为B，记表示数x的点为C，点C是数轴上的一个动点。“数轴”是初中数学中最基本的数形结合，也是初中数学中最早运用数形结合的一个例子。绝对值表示数轴上的一个点到原点的距离，而用两数的差的绝对值表示数轴上两点之间的距离。根据题意，画出简易数轴：

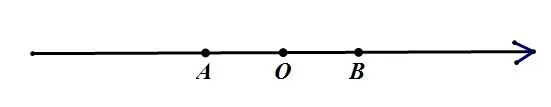
我们可以发现，点A和点B将数轴分成了三段，根据动点C的三个不同位置画出三种不同情况下的数轴再一一进行分析。此时，这个问题就转化为线段CA+CB＞5 的题目了。

通过观察三张图可以发现：当点C运动到点A和点B之间时，线段CA+CB=5；当点C运动到点A的左边或者点B的右边时，线段CA+CB＞5。

所以，我们就有结论：当-2 ≤x≤3 时，|x+2|+|x-3|=5；当x＜-2或x＞3 时，|x+2|+|x-3|＞5。

二、数形结合在二次函数中的应用

例2：已知点A（-1，y1）、B(-3，y2)、C(-2，y3)、D(1，y4)在函数y=x2+2x+2 的图像上，比较y1、y2、y3、y4的大小。

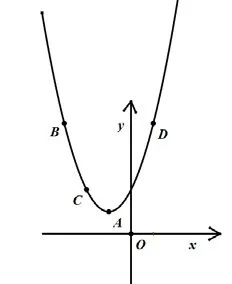
分析：我们已经学过了二次函数的图像，根据函数表达式画出函数图像，描出A、B、C、D这四个点的相应位置。那么，要比较y1、y2、y3、y4的大小就是看这四个位置的高低。如图所示：

通过图像，我们就可以马上看出y1＜y2＜y3＜y4。用这样的方法解决问题，就使得数学更形象、更直观，数学就不那么枯燥了，数学也有美的一面，也让那些后进的学生感觉到数学很有趣。

三、数形结合在数列计算中的应用

分析：我们可以这样解：

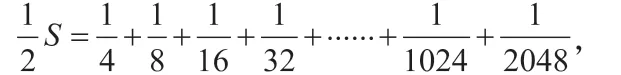
我们还可以试着通过图形来理解。画一个正方形，把这个正方形一分为二就得到，把其中一半再一分为二就得到，把的一半再一分为二就得到……画完图形之后我们可以发现：这些全部加起来就是用整个正方形减去右下角的最后一块小正方形，也就是。如图所示：

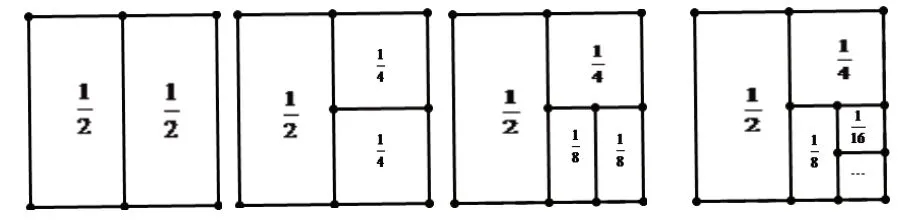
这样的方法既简单又直观，容易理解，同学们一看就知道了，充分展现了数形结合的优势和奇特之处。

四、数形结合在勾股定理中的应用

分析：对于初中生来说，这种类型的题目是非常新颖的，以前没有见到过。同样，我们可以根据题意，构造一个图形，将题目转化成图形来解决。

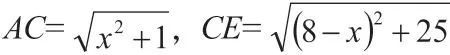
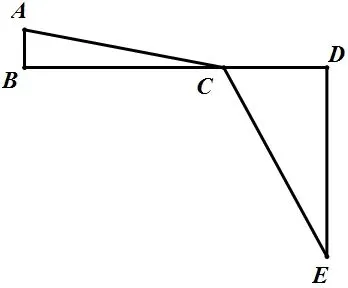
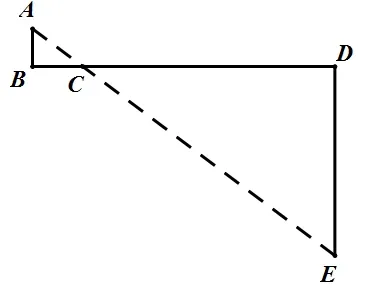
此时，上述问题就转化成求AC+CE的最小值的问题了。到了这一步，同学们很容易想到：两点之间线段最短。要求AC+CE的最小值，只需要连接AE，线段AE 与线段BD 的交点就是动点C 的位置。此时AE 的长度就是AC+CE 的最小值。如图所示：

之后，过点A作AF平行且等于BD，连接BF，则在直角三角形AFB中，利用勾股定理即可求出线段AE的长度，也就是线段AC+CE的最小值。如图所示：

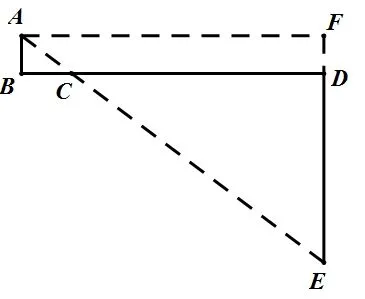
如此，运用图形将学生束手无策的最小值问题转化成了熟悉的勾股定理的问题，不仅方便同学们理解，还降低了计算的难度，提高了做题的正确率。

在教学过程中，老师应鼓励学生多利用图形去研究、探索问题，培养学生的创造性思维和开放性思维，使同学们对数学学习更有兴趣。

总之，作为一名初中数学教师，应该在传授知识的同时，提高学生数形结合的能力，从“数”的方面、“形”的方面深化理解，形成直觉思维，从而顺其自然地找到解题方法。在日常教学的过程中，教师要尽量利用多媒体教学，充分体现数字和图形之间的联系和变化规律，使学生理解更深刻，更灵活地掌握方法，充分观察图像，不管是静态的还是动态的图像，对它们的特点观察得越仔细，思考得越深入，那么认识也就比较深刻，这样遇到相关联的情景时才能够产生灵感，找到切入点解决问题。

当前，素质教育已经成为主流，对学生进行综合素质和能力的培养是建设创造性人才的需要。拥有创造性思维的人，才能更好地在各自的领域内有所创新，推动科学技术和社会向前发展。教师应该发挥外因的作用，积极引导学生的兴趣，发挥学生自主学习的内在动因，学生才能长久受益。