高中数学解题中整体思想的运用管窥

江苏省扬州市邗江区瓜洲中学 刘桂龙

真正成功的高中数学教学不是单纯地讲解课本知识，而是让学生掌握数学解题方法，教师应引导学生加强对数学思想方法的学习，如此学生在今后的学习中遇到相似问题时就会迎刃而解。整体思想是一种重要的解题思想，是指从整体角度出发看待问题，发现问题的整体结构特点，把握各个组成部分之间的关联，对问题进行有意识的整体处理的一种思想方法。高中数学教师需要认识到整体思想的重要性，灵活应用整体思想，帮助学生培养整体解题思路，如此才能实现事半功倍的教学效果。

一、借助整体思想，化解椭圆问题

椭圆是高中数学知识体系的重要组成部分。椭圆问题非常复杂，且计算量也很大，面对椭圆问题，很多学生都表示无从下手，头痛不已，椭圆问题已经成为教学难点。为了帮助学生更好地解决椭圆问题，教师可引导学生灵活运用整体思想，借助整体思想简化椭圆问题，帮助学生抓住解决问题的关键，从而更好地提升学生解题能力。

二、借助整体思想，化解三角函数问题

三角函数一直是高中数学知识体系的重要组成部分，也是高考的重头戏。三角函数题目往往变化多端，让学生摸不着解题头脑。化解三角函数问题的一个重要方式就是利用整体思想，把几个变量通过整体设元的方式，构建一个新的解题方程，从而实现化难为易的解题效果。当然，这需要教师引导学生体会整体思想在三角函数中的积极意义，如此才能帮助学生深入理解整体思想。

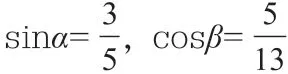
在上述案例中，教师根据整体思想，把α-β、cosαcosβ、sinαsinβ看成一个整体，从而根据三角函数关系式求出问题答案，如此可以让三角函数问题变得更为简单易懂，有助于提升学生解题效率。

三、借助整体思想，化解立体几何问题

立体几何知识是高中数学知识体系的另一重要内容。在解决立体几何问题的过程中，切忌将知识点分开来看，而是应当从整体角度思考各个知识点之间的关系，如此才能减少解题过程中的疏漏，实现顺利求解的目标。在立体几何教学中，教师可借助整体思想，引导学生系统思考立体几何知识体系，帮助学生全面看待立体几何知识，从而促使学生不断完善解题思维。

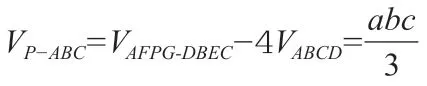
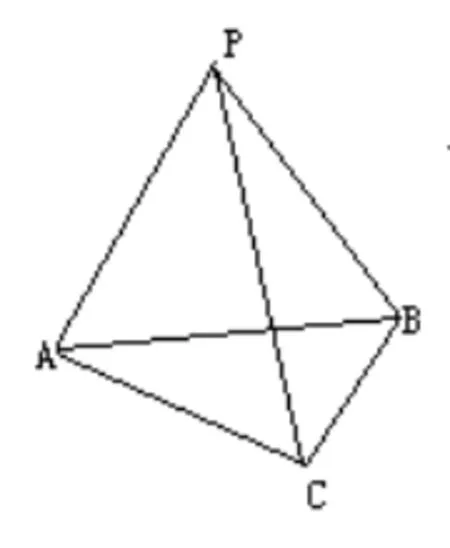
图1

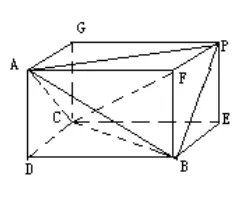
图2

当然，在立体几何教学中，教师也可以利用整体思想帮助学生构建立体几何知识体系。比如，当学生学习完了平行知识之后，教师应当引导学生对线线平行、线面平行、面面平行进行整体、全面的思考。比如，通过“a∥b，b∥c，则a∥c”这个线线平行原理，联想到“a∥面b，c∥面b，则a∥c”这个线面平行原理，如此可以帮助学生构建系统的立体几何知识体系，促使学生更好地解决立体几何问题。

在上述案例中，教师根据整体思想，把三棱锥当作长方体的一部分来看，利用割补法进行体积转化来实现化难为易，如此可以让立体几何知识变得更为简单明了，从而帮助学生掌握解决立体几何问题的关键。

总而言之，整体思想是一种有效的解题思想。在高中数学教学中，教师需要重视整体思想，通过整体思想与三角函数知识、椭圆知识和立体几何知识之间的渗透融合，帮助学生掌握整体思想的精髓，促使学生灵动提升解题能力，从而更好地提升高中数学教学效率。值得注意的是，整体思想只是高中数学解题思想的内容之一，诸如数形结合思想、化归思想和分类与整合思想等数学思想也在培养学生解题能力方面发挥了巨大作用，教师只有结合数学知识，引导学生系统掌握各种解题思想，才能真正实现提升学生解题效率和速度的目标。