基于迭代插值的实复转换频率估计算法

陈 鹏, 涂亚庆, 李 明, 张海涛

(陆军勤务学院 军事物流系，重庆 401311)

实信号的频率估计广泛应用于雷达、通信与仪表装置等领域，具有重要的理论研究意义和实际应用价值[1-2]。例如，线性调频连续波(Linear Frequency Modulation Continuous Wave, LFMCW)雷达就是通过估计采样信号的频率来测量目标距离。因此，提高采样信号的频率估计精度有利于改善LFMCW雷达的测距精度[3]。

目前，针对实信号的频率估计算法得到了广泛研究，主要可分为时域法和频域法两类。时域法主要是基于信号自相关的频率估计算法，如扩展自相关法、相频匹配法等。频域法主要是基于DFT(Discrete Fourier Transform)的频谱分析法，如极大似然法，加窗插值法等。

文献[4]提出一种基于扩展自相关的频率估计算法，该算法采用粗估计和精估计两步法估计频率。首先对采样信号进行两次自相关计算，得到频率粗估计值，然后根据最小二乘法构造误差函数，通过最小化误差函数得到频率精确估计值。该算法提高了频率估计精度，但受信号非整周期采样影响，且在中高信噪比时，估计精度较低。在此基础上，文献[5]提出一种相频匹配频率估计算法，首先利用两步自相关法进行频率粗估计，消除信号非整周期采样的影响，然后生成参考信号，并利用柯西不等式构造误差函数，通过最小化误差函数实现频率精估计。该算法克服了信号非整周期采样的影响，但运算量大，实时性差，不利于实际应用。

时域法易受信号非整周期采样影响，抗干扰性不强，或计算量较大，实时性较差。而频域法容易借助硬件实现，计算速度快，且具有更好的抗噪性，受到了广泛的研究[6]。

在高斯白噪声背景下，极大似然法通过寻找信号周期图上最大值点来计算信号频率[7]。该算法在处理复信号时，其估计效果最好，但计算量大，不利于实际应用。当处理实信号时，受信号中负频率成分的影响，在中高信噪比条件下的频率估计精度降低。文献[8]通过加窗来抑制实信号中负频率成分的影响，并采用频谱插值来减少信号频谱泄露，降低了负频率的影响，但当信号频率较低时，受窗函数主瓣干涉的影响，频率估计精度较低，存在估计偏差。文献[9]提出一种滤除负频率成分的频率估计算法，通过粗估计信号频率生成参考信号，并与采样信号相乘实现频谱搬移，以滤除直流分量的形式降低负频率的影响，并采用高精度的复信号频率估计算法实现频率估计，该算法计算量低，精度较好，但在低频与高信噪比时，频率估计精度较低。

针对频域法易受实信号中负频率成分影响的问题，本文在频谱分析法的基础上，提出一种实复转换频率估计算法，给出算法原理和计算的具体流程，并进行计算验证和实验验证。

1 频域法分析

1.1 信号模型

采样信号模型如式(1)所示。

x(n)=acos(ωn+θ)+z(n)n=0, 1, …,N-1

(1)

式中：ω=2πf/fs为信号圆周频率，f与fs分别为信号的模拟频率和采样频率，由采样定理可知fs>2f，则ω∈(0,π)，rad；a>0和θ∈(-π,π)分别为采样信号的幅度和初相位；N为信号长度；z(n)为均值为0，方差为σ2的高斯白噪声；采样信号的信噪比为SNR=a2/2σ2。

在频谱分析中，采样信号频率可用式(2)表示

ω(k0+δ)ωs

(2)

式中：ωs为频率分辨率，ωs=2π/N；k0为信号频谱中能量最大值点，k0=[ωN/2π]；[t]为取最接近于t的整数；δ为频率偏差，-0.5≤δ≤0.5。

1.2 存在问题分析

根据欧拉公式

acos(ωn+θ)=Aeiωn+A*e-iωn

(3)

式中：A为复幅值，A=0.5aeiθ;A*=0.5ae-iθ,A与A*互为共轭。

从式(3)可以看出：无噪实正弦信号含有正频率和负频率两种频率成分。由于二者相互影响叠加，使得频率估计时存在偏差。

对x(n)进行DTFT计算

(4)

当ω=kωs时，即δ=0，|X+|取得最大值，受负频率成分的叠加影响，|X|不能取得最大值。因此，用频域法估计频率存在偏差。当ω≠kωs时，即δ≠0，|X+|不能取得最大值，受负频率成分的影响，|X|也不能取得最大值，因此频率估计存在偏差，且实际应用中δ常常不为0。

对于各类频率估计算法的性能，可用统计信号的无偏估计下限(克拉美罗下限(Cramer-Rao Lower Bound,CRLB))来检验[10]。单频实信号的频率估计下限为

(5)

2 实复转换频率估计算法

为消除实信号中负频率成分的影响，本文提出一种基于迭代插值的实复转换频率估计算法。下面分别从算法原理和具体算法两方面进行介绍。

2.1 算法原理

所提算法的核心思想是将实信号转换为复信号，再对复信号进行处理，以消除实信号中负频率成分的影响，其原理如图1所示。

首先，将采样信号进行90°相移，生成正交分量。然后，将采样信号与其正交分量合成为复信号，实现实复转换，以减少实信号中负频率成分对频率估计的影响。

图 1 算法原理Fig.1 Algorithm schematic diagram

最后，采用迭代插值估计算法对复信号进行频率精估计，重新生成采样信号的正交分量和复信号。再对复信号进行处理，以极大程度地消除实信号中负频率成分对频率估计的影响，最终得到频率的精确估计值。

2.2 频率估计算法

2.2.1 频率粗估计

首先，利用FFT算法对采样信号x0(n)进行预处理，得到频率粗估计值。

(6)

(7)

(8)

2.2.2 频率精估计

采用复信号中的AM迭代算法思想[11]，利用式(9)～式(15)完成信号的频率精估计。

(9)

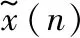
(10)

(11)

利用式(12)与式(13)对合成的复信号进行频谱两点插值，求取信号频率偏差。

(12)

(13)

根据频率偏差，利用式(14)计算信号频率值。

(14)

2.3 算法流程

综上所述，基于迭代插值的实复转换频率估计算法的计算流程如下：

步骤1利用式(6)与式(7)对采样信号进行频率粗估计，并利用式(8)生成参考信号；

步骤2利用式(9)实现采样信号90°相移，得到其正交分量，并利用式(10)实现实复转换，得到复信号；

步骤3利用式(12)和式(13)计算信号频率偏差，利用式(14)得到较精确的频率估计值；

步骤4重复步骤2和步骤3，得到精确的频率估计值。

3 计算验证

不失一般性，在仿真时，实信号的幅度设为1，初相位θ∈(-π,π)随机取值，每组实验各进行1 000次蒙特卡罗实验。RCSD法与本文算法均属于迭代插值算法，均采取2次迭代，即I=2。

3.1 不同信噪比

为说明所提算法在不同信噪比下的频率估计性能，设N=64，ω=2π/9，在SNR由0 dB以步长2 dB递增到70 dB的条件下进行了仿真实验，实验结果如图2所示。

图2 不同信噪比下的频率估计结果Fig.2 Frequency estimation results on different SNRs

从图2中可以看出：EA法在低信噪比时的估计精度较好，当SNR>10 dB时，估计效果逐渐饱和，估计精度最差。SINW法在中低信噪比下的估计精度较好，但与CRLB存在约4 dB的偏差，当SNR>50 dB时，估计精度逐渐饱和；MPHD法在低信噪比下的估计精度较差，当SNR>8 dB时，其估计精度随信噪比的增加而提高，与CRLB存在约1 dB的偏差；RCSD法在低信噪比下具有较高的估计精度，接近CRLB，优于MPHD法，但当SNR>44 dB时，其估计效果逐渐趋于饱和；本文算法在整个信噪比范围内均具有高精度估计性能，始终接近于CRLB，优于EA法、SINW法以及MPHD法，当SNR<40 dB时，本文算法与RCSD法具有相当的估计性能，当SNR>40 dB时，本文算法优于RCSD法，且随着信噪比的增加，本文算法的优势更加明显。

3.2 不同信号频率

为说明所提算法在不同频率下的频率估计性能，设N=64,SNR= 40 dB，在频率由0.04π以步长0.02π递增到π的条件下进行了仿真实验，实验结果如图3所示。

从图3中可以看出：EA法受信号非整周期采样影响严重，估计效果呈波动状态，差于其他几种算法；SINW法在0.04π～0.84π频率范围内的估计效果大致相当，优于EA法，与CRLB存在约3.5 dB的偏差，当频率大于0.84π时，其估计精度随频率增加而逐渐降低；MPHD法在频率为0.04π～0.9π时，估计精度较高，优于EA法和SINW法，与CRLB存在约1 dB的偏差，当频率大于0.9π时，估计精度降低；RCSD法在频率范围为0.18π～0.82π时的估计精度均优于MPHD法，当频率低于0.18π或高于0.82π时，RCSD法的估计精度低于MPHD法与本文算法；本文算法在0.04π～0.9π内的估计精度最高，优于其他几种算法，更加接近CRLB，当频率大于0.9π时的估计精度略低于MPHD法。

图3 不同频率下的频率估计结果Fig.3 Frequency estimation results on different frequencies

3.3 不同频率偏差

为说明所提算法在不同频率偏差下的频率估计性能，设N=128,SNR=40 dB，k0=4，在δ由-0.5以步长0.025递增到0.5的条件下进行了仿真实验，实验结果如图4所示。

从图4中可以看出：EA法、SINW法与RSCD法的估计结果受频率偏差影响较大，呈波动状态，EA法在δ=±0.25时，估计效果最好；SINW法在δ=±0.5和δ=0.1时，估计效果最好；RCSD法优于EA法与SINW法；MPHD法与本文算法的性能优于其他几种算法，更接近CRLB，当频率偏差为-0.25≤δ≤0.25时，MPHD法优于本文算法，当频率偏差为-0.5≤δ≤-0.25与0.25≤δ≤0.5时，本文算法优于MPHD法。

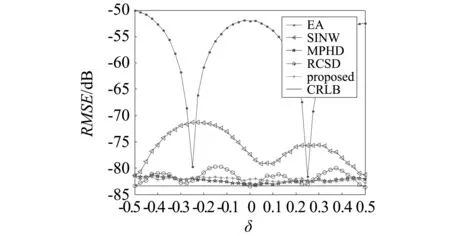
图4 不同频率偏差下的频率估计结果Fig.4 Frequency estimation results on different frequency offsets

3.4 不同信号长度

为说明所提算法在不同信号长度下的频率估计性能，设SNR=40 dB，ω=0.146π，在N由32以步长8递增到256的条件下进行了仿真实验，实验结果如图5所示。

图5 不同信号长度下的频率估计结果Fig.5 Frequency estimation results on different signal lengths

从图5中可以看出：EA法受信号非整周期采样的影响，估计效果差于其他方法，且呈周期性波动；SINW法优于EA法，与CRLB存在约3.5 dB的偏差；MPHD法的估计精度随信号长度增加而提高，且没有明显波动，接近于CRLB；RCSD法在N>64时的估计精度均优于MPHD法，当信号较短时，其估计性能有所下降；本文算法在信号较长时，其估计性能与RCSD法相当，优于其他几种算法，在信号较短时，本文算法的估计性能具有明显的优势，优于其他算法，提升了算法的实时性。

4 实验验证

为检验所提算法的实际测量效果，利用项目组自研的LFMCW雷达实验平台进行了测距实测实验，雷达各参数设置如表1所示，实验现场如图6所示。

表1 雷达参数设置值

图6 测距实验现场Fig.6 Ranging experiment field

根据LFMCW雷达测距原理，测量距离可由式(15)进行计算。

R=ωfsCT/4πB

(15)

式中：R,fs,C,T,B分别为测量距离、采样频率、电磁波传播速度、调频周期和调频带宽。

设实验的测距范围为5～10 m，间隔1 m，利用DEVONL80手持激光测距仪和田岛L-50U玻璃纤维标尺来测量实际距离。为了验证本文所提方法的有效性，和仿真实验中较好的两种方法，即MPHD法和RSCD法进行了比较，实验结果如表2所示。从实测实验结果可以看出：运用本文所提算法的测量结果比运用MPHD法和RSCD法的测量结果更接近实际距离，与仿真实验结果一致。本文所提算法的平均绝对误差为0.022 m，MPHD法和RSCD法的平均绝对误差分别为0.041 m和0.034 m。因此，本文所提算法具有更低的测量误差，比MPHD法和RSCD法更有效，改善了LFMCW雷达的测距性能。

表2 测距结果

5 结 论

为消除实信号中负频率成分对频率估计性能的影响，本文提出了一种基于迭代插值的实复转换频率估计算法，该算法通过将实信号转换为复信号的形式，并对复信号进行迭代插值得到频率估计值。

计算验证表明：本文所提算法有效的消除了负频率成分对频率估计的影响，其频率估计性能在不同的条件下均优于其他算法，或与目前最优秀的算法具有相当的性能。特别地，当信号频率较低时，优势更加明显，并提升了算法的实时性，改善了算法的抗噪性，提高了估计精度，使得频率估计值的均方误差更接近于克拉美罗下限。并在LFMCW雷达实验平台进行了测距实验，验证了本文算法的有效性，优于MPHD法和RCSD法。