随机结构主动控制系统的鲁棒控制研究
2019-10-10赵时运周福霖
王 磊, 谭 平, 赵时运, 陈 刚, 周福霖
( 1. 广州大学 工程抗震研究中心,广州 510405; 2. 安徽水利开发股份有限公司,合肥 230031;3. 安徽建工集团有限公司,合肥 230031)
自1972年Yao[1]结合现代控制理论提出结构振动控制概念以来,结构振动控制从理论到应用都取得了很大进展。其中,主动控制作为一种现代化程度最高,更为积极主动的土木工程结构防灾策略,受到世界各国学者的广泛研究。在结构振动控制理论最初的研究中,以经典随机最优控制理论为代表的主动控制方法多是基于确定性结构模型、在特定激励时程或随机激励模型下进行控制系统设计,由此建立的控制系统控制效果完全依赖于被控对象和外界干扰的数学模型,但在实际中,由于非完备观测和非完全控制的存在,结构的物理参数难以精确地确定,在结构不确定性因素的干扰下,控制系统的控制性能和稳定性很难得到保证[2]。因此,不确定性系统的鲁棒控制问题已成为结构振动控制领域研究的热点问题之一。但是在以往的控制系统鲁棒性研究中,研究者们基于有界不确定性结构模型讨论较多[3-9],对随机结构模型研究较少。但对于实际结构或多或少都具有一定的随机性[10],如果直接以现有不确定性模型鲁棒控制理论进行随机结构的控制设计,其结果将相对保守,造成控制能量的浪费[11]。因此,对于随机结构的鲁棒控制问题值得进一步地深入研究。
本文针对随机系统的鲁棒控制问题进行了一些初步的研究,提出了基于线性矩阵不等式(Linear Matrix Inequality,LMI)和随机结构正交展开理论的鲁棒H∞控制系统设计方法,该方法以随机结构正交展开扩阶模型为基础,结合有界实引理和线性矩阵不等式,建立鲁棒控制系统,并使得控制系统传递函数对不确定性扰动满足H∞干扰抑制。最后,以某典型随机框架结构为例,结合概率密度演化方法,比较了不同鲁棒H∞控制系统对于随机响应的控制效果,验证了本文所述方法的有效性和适用性。
1 随机结构控制系统模型
1.1 运动方程
对于n自由度随机结构控制系统,其运动方程为

(1)
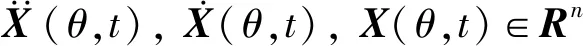
1.2 扩阶模型
不失一般性,假设式(1)中随机结构的质量、阻尼和刚度具有下列形式
(2)
(3)
(4)
式中:M0,C0,K0,M′i,M″i,C′j,C″j,K′l,K″l为质量、刚度、阻尼部分的确定性矩阵;θi(i=1,2,…,N1+N2+N3)为结构中服从λi-PDF分布的相互独立的有限随机变量, 其随着λ取值不同,分别具有不同的分布形式, 关于λi-PDF分布的详细介绍可参阅文献[15]。
对于式(1)结构响应可基于随机结构正交展开理论,利用Gegenbauer多项式近似表示为
(5)

把上述式(2)~式(5)代入式(1),进一步利用Gegenbauer多项式一次和二次递推关系式,式(1)可转化为均方残差最小意义下的确定性扩阶系统

(6)

2 基于LMI的鲁棒H∞控制器设计
对于式(6)可转化为如下状态空间描述
(7)


(8)
对于控制系统式(8)由w(t)~Y(t)的闭环传递函数为
(9)


(10)
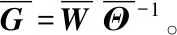
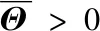
(11)
求解式(11)即可得到满足要求的随机结构鲁棒H∞控制系统。
3 随机结构概率密度演化分析
对于式(1),在确定性初始条件下,其解存在、唯一且连续的依赖服从λ-PDF分布的随机参数θ。 根据广义概率密度演化方程,结构响应X的第j分量Sj和θ的联合概率密度函数psjθ(sj,θ,t)有[17]
(12)
利用有限差分法[18]求解式(12)即可得Sj概率密度函数
(13)
式中:Ωθ为前述服从λ-PDF分布的结构随机参数θ的PDF分布区域。
对于结构响应极值的概率分布可以建立相应的伪随机过程
(14)
Y(τ)=Zext·τ
(15)
式中:τ为伪时间步,利用式(12)及有限差分法数值求解可得
(16)
则相应极值概率密度分布为pZext(z)=pY(y,τ)|τ=1,y=z。
4 仿真分析
取三层框架结构,结构顶层设置AMD控制系统,其刚度、阻尼按最优TMD参数设计[19],控制力峰值取为25 kN,结构名义模型参数和AMD参数如表1所示。假设结构的一层刚度k1具有随机性,其概率密度函数如式(17)所示,概率密度曲线如图1所示。
(17)


结构层间位移是反映结构是否安全的一项重要指标,因此本文以结构层间位移作为AMD系统的控制对象,同时为兼顾考虑控制能量,其输出矩阵C1,D1,D2定义如下
式中:a1,a2,a3分别为各层层间位移相对重要性系数,其值分别取为1.5,1和2;a4为考虑能量输入的相应系数,取为1×10-5。

选取图2所示的El Centro(NS)地震波作为外激励,其地震动峰值设为0.1g。对于概率密度演化方法(PDEM)选取5个概率代表点进行计算,其计算结果如图3~图5和表2~表4所示。

表1 名义结构参数

图1 概率密度曲线Fig.1 PDF curve

图2 地震动时程曲线Fig.2 Time histories of El Centro
图3和图4分别给出了随机结构一层层间位移响应的均值和标准差,其他各层响应均值、标准差和均方根如表2所示。通过对前述图表分析可以发现:①概率密度演化方法与蒙特卡罗法计算结果差异较小(以无控结构响应为例),说明概率密度演化方法具有较好的计算精度;②三种控制系统对于随机结构响应均值、标准差和均方根都有较好的控制效果,在整个时程范围内,控制系统都将随机结构响应的概率密度限定在较小的区间内进行演化,减小了响应的离散性。

图3 一层层间位移响应均值Fig.3 The mean of the inter-story drift of the first floor
图5(a)和表3、表4分别给出了结构层间位移响应峰值的概率密度分布和相应的数字特征。通过对表3分析可知除二层响应峰值标准差外,控制系统对于结构响应峰值均值、标准差和均方根都具有较好的控制效果,再结合图5(a)分析可知,虽然控制系统放大了二层响应峰值的标准差,但由于控制系统降低了响应峰值的均值,因此仍增大了结构的动力可靠性。对表4中响应峰值变异系数的比较可以发现,虽然控制系统增大了峰值响应的变异性,但控制力减小了各层响应峰值变异系数的差异性,即刚度的随机性对于结构响应峰值的影响更为均匀。
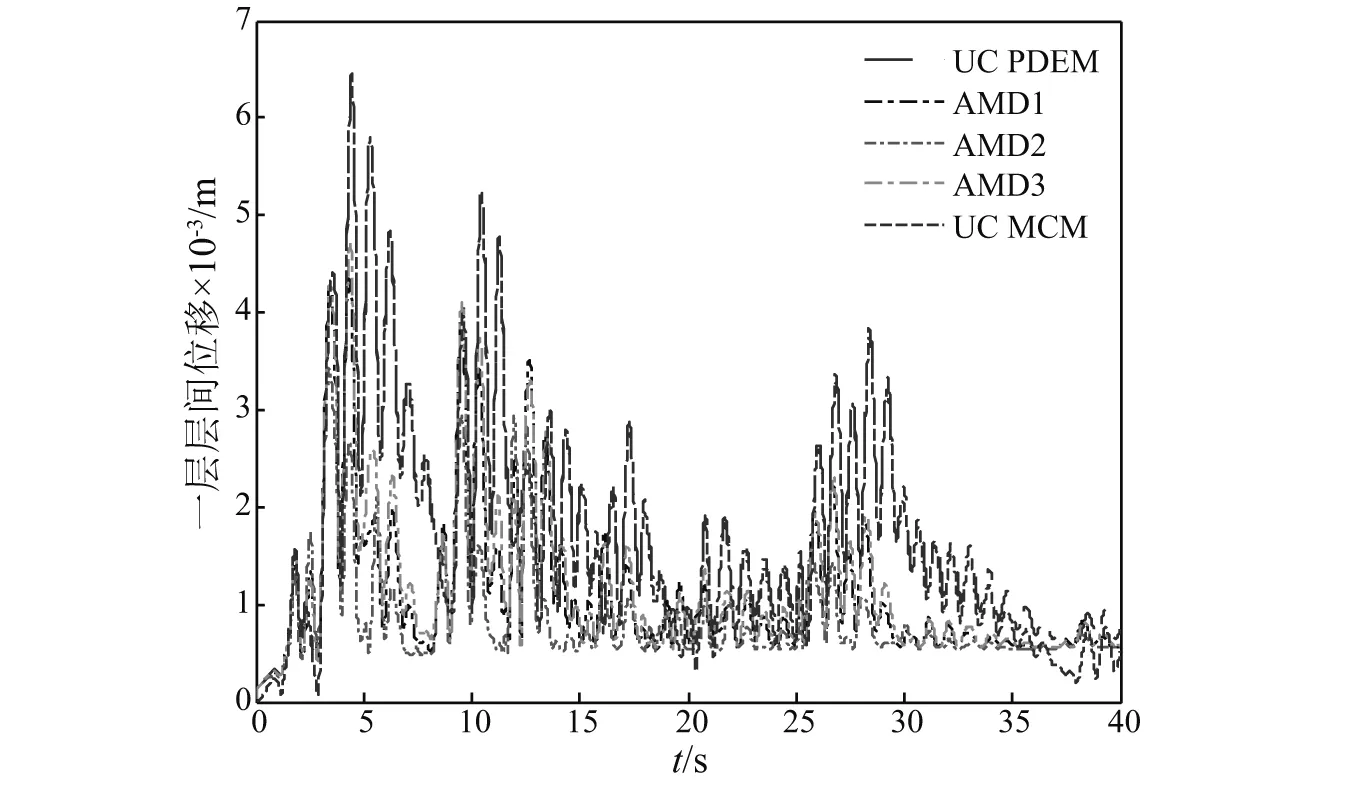
图4 一层层间位移响应标准差Fig.4 The standard deviation of the inter-story drift of the first floor

图5 El Centro 波作用下极值概率密度曲线Fig.5 The probability density curves of the extreme value of the structure under El Centro earthquake
通过前述分析可以看出三种鲁棒H∞控制系统都能有效抑制随机结构响应,即控制系统对于结构的随机性具有较好的鲁棒性。为了进一步的比较各控制系统的差异,以下将以均方根作为控制指标进行比较。因为在随机结构控制系统设计中,随机响应的均方根相较于均值和标准差,能更为全面的反应控制系统的控制效果而常作为设计者们关注的重点。从表2和表3中可以看出,对结构一、二两层层间位移响应和响应峰值,AMD3具有仅次于AMD2的控制效果。而对结构顶层响应,AMD1控制效果最优,AMD2和AMD3次之且控制效果差异较小。再结合图5(b)分析可知在整个控制过程中,AMD2所需控制能量最多,AMD3最少,即AMD3以最少的控制能量取得了优于AMD1的控制效果。
通过如上比较分析可以发现,在三种AMD控制系统中,AMD1控制效果的鲁棒性相对较差;而AMD2设计相对保守,需要较大的控制能量以保证控制系统的控制效果;本文所述方法设计的AMD3以最少的控制能量较为理想的抑制了随机结构响应,控制效果鲁棒性较好。
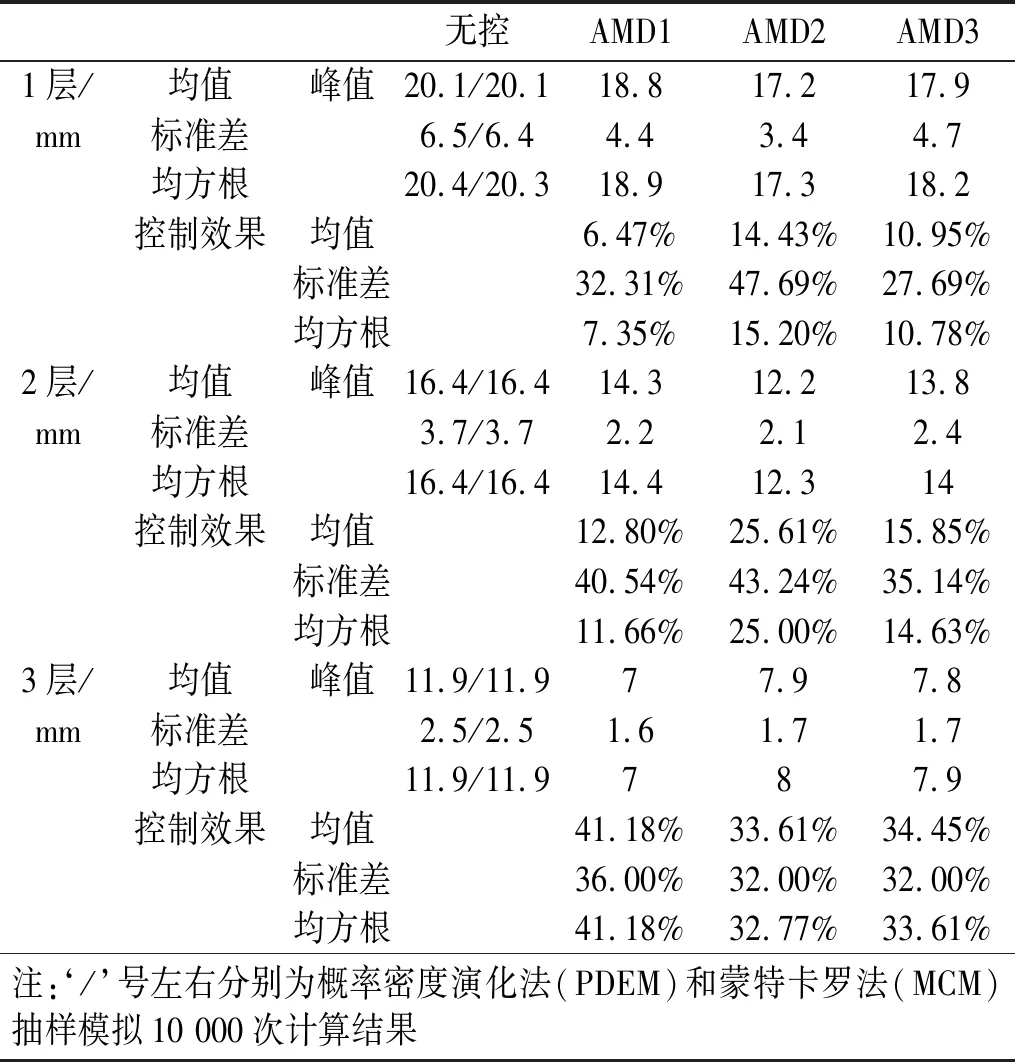
表2 El Centro波作用下随机结构层间位移响应

表3 El Centro波作用下随机结构层间位移响应峰值

表4 响应峰值的变异系数
5 结 论
本文以随机结构的正交展开扩阶模型为基础,结合线性矩阵不等式(LMI)和概率密度演化方法,研究了随机结构的鲁棒H∞控制问题,得到了以下一些主要结论:
(1) 相较于无控系统,三种鲁棒H∞控制系统对于结构层间位移响应均值、标准差和均方根都具有较好的控制效果,在整个时程范围内,控制系统都将随机结构响应的概率密度限定在较小的区间内进行演化,减小了响应的离散性。
(2) 三种鲁棒H∞控制系统都能够有效地抑制结构层间位移响应峰值,在增强结构的可靠性的同时,减小了结构各层响应峰值变异系数的差异,从而使得刚度的随机性对于响应峰值的影响更为均匀。
(3) 以结构名义模型设计的控制系统,由于忽略了结构参数的随机性,其鲁棒性相对较差;而以结构最不利状态设计的控制系统,因为设计的保守性,在控制过程中需要以较大的能量来保证控制系统的控制效果;本文所述方法设计的控制系统以合理的控制能量利用效率较为理想的抑制了随机结构响应,控制系统鲁棒性较好。
