压电阻抗损伤识别温度影响的协整消除方法研究
2019-10-10李秀娟屈文忠
李秀娟, 屈文忠, 肖 黎
(武汉大学 工程力学系,武汉 430072)
近年来,结构健康监测技术在国内外得到大量的研究和广泛的应用[1-2]。结构健康监测与损伤识别研究中广泛采用压电高频机电阻抗方法(Electromechanical Impedance,EMI)。利用压电材料的特性与波动理论,得到结构的动态阻抗信息,根据阻抗谱的频移和幅值变化,以及其他损伤指标判断结构是否损伤[3]。该方法有许多优点,可以识别局部损伤,进行损伤定位;工作频段较高,对微小损伤敏感;同时压电元件激励电压低,尺寸小,成本低廉,所以在结构健康监测领域,压电阻抗方法应用前景广泛[4]。
在压电阻抗方法中,所建立的损伤特征量不仅仅与结构损伤有关,还会受到环境温度的影响。温度对损伤特征量的影响甚至会完全淹没损伤影响,造成损伤误判,因此,有效消除温度影响至关重要。Sun等[5]利用基准和测量信号之间的互相关分析来补偿阻抗谱的频移;Park等[6]利用修正的RMSD(Root Mean Square Deviation)系数,进行频率和幅值的同时补偿;Koo[7]在Park等的基础上将获得最大互相关系数的频移利用有效频移(Effective Frequency Shift,EFS)进行温度补偿;Baptista等[8]同样利用互相关偏差度量指标(Correlation Coefficient Deviation Metric, CCDM)进行有效频移补偿温度效应。与以上温度补偿方法不同,本文利用协整思想消除EMI损伤检测技术中温度效应。该方法不需记录环境温度值,不必确立相关参数与温度关系便可消除长期监测过程中的环境温度影响,且对微小损伤敏感,表征结构损伤的效果明显。
协整思想来源于计量经济学,它将不平稳阶数相同的时间序列线性组合为一个平稳的时间序列,由此消除时间序列的不平稳性。协整理论已经被国内外学者引入结构健康监测领域里,用于处理环境因素的影响。Liu 等[9]将协整变量取为应变,Cross等[10-11]将协整变量分别取为频谱幅值和频率,以此消除了环境因素的影响,准确识别出损伤发生;刁延松等[12]以结构加速度响应数据第一阶AR 模型系数选为协整变量去除了温度、质量对结构损伤识别的影响;梁亚斌等[13]以固有频率作为协整变量,消除了温度对损伤识别的影响;何浩祥等[14]以自然环境下的混凝土桥梁为研究对象,基于协整思想建立了其温度、湿度、一阶固有频率之间的长期均衡关系,进而得到了消除温度和湿度影响的频率修正模型,有效消除了多环境因素对损伤检测的影响。近年来结构健康监测与损伤识别研究中广泛采用压电高频机电阻抗方法(EMI),上述研究中没有涉及EMI中的协整研究,本文将协整思想应用于EMI方法,以阻抗谱峰值频率作为协整变量进行研究,以消除其环境温度影响,准确识别损伤。
1 压电阻抗方法及温度影响
1.1 压电阻抗方法基本原理
结构损伤会使其机械阻抗发生变化,但机械阻抗不易直接测得。将压电片粘贴于结构表面或埋置于结构内部,施加高频电压激励压电片,由于逆压电效应,压电片会产生振动,并且会带动主体结构振动;主体结构的振动又会影响压电片的振动,由于正压电效应,压电片会产生电信号,从中提取的电阻抗信号便包含主体结构的损伤信息。
对于压电片与结构系统构成的单自由度弹簧-质量-阻尼(Spring-Mass-Damper, SMD)系统模型,其耦合电导纳表达式为[15]
(1)

由式(1)可以看出,压电系统耦合电导纳包含结构的机械阻抗信息,结构损伤时,其机械阻抗会发生变化,可以通过耦合电导纳反映出来。在压电阻抗方法中,通常会用导纳实部信息作为损伤指标判断结构是否损伤,这是由于其实部对结构的完整性更加敏感,而其虚部对黏结层特性和温度变化比较敏感。对电导频谱进行分析时,可以利用其频谱偏移、幅值等特性来判断结构是否损伤。扫描频率一般选择为30~500 kHz,在具体选择时,要尽量包含结构的高阶固有频率。
1.2 温度影响

2 协整基本原理
2.1 协整思想
协整思想用于处理非平稳问题,其基本思想为:选取协整变量,得到若干个非平稳的时间序列,若它们之间存在长期均衡关系,则可以将它们线性组合为平稳的时间序列,消除时间序列的非平稳性。
对于不平稳的时间序列yt, 其中,t=1,2,3,…,若其前d-1阶差分均不平稳, 而d阶差分平稳,那么就称该时间序列的不平稳阶数为d阶, 此时, 称它为d阶单整时间序列, 记作yt~I(d)。I(0)指平稳的时间序列。
时间序列可以协整需要两个前提条件[16]: ①时间序列的不平稳阶数相同;②时间序列的变化趋势相同。
2.2 ADF检验
ADF(Augmented Dickey-Fuller)检验是一种平稳性检验,用于确定时间序列的平稳性及不平稳阶数。在执行ADF检验时,首先需要对时间序列进行回归分析,建立其AR(p)模型
yt=c+dt+ayt-1+b1Δyt-1+…+
bpΔyt-p+e(t)
(2)
式中:p为滞后长度,p个滞后项保证了误差项et是白噪声, 即et~(0,σ2),且相互独立;c为漂移项; dt为趋势项,可以根据时间序列的数据特征判断这两项是否存在。
对于上述AR(p)模型, 当|a|<1时,yt是平稳的; 当a=1时,yt是不平稳的; 当|a|>1时,时间序列是爆炸的,没有意义。确定了合适的滞后长度和模型类型后,利用最小二乘法估计AR(p)模型的系数,然后执行显著性检验判断序列平稳性。若时间序列非平稳,则对其作差分,对差分序列进行平稳性检验,重复上述过程直至序列是平稳的,便可以确定时间序列的不平稳阶数。
2.3 Johansen检验
Johansen检验用于判断时间序列是否可以协整,并计算协整向量。
假设Yt=[y1t,y2t,…,ynt]′, 其中y1t,y2t,…,ynt均为一阶单整序列,且变化趋势相同,首先建立其向量误差修正模型
ΔYt=ΠYt-1+Γ1ΔYt-1+…+Γp-1ΔYt-(p-1)+
DX+εt
(3)
式中:Π为长期均衡矩阵;Γk为短期动态矩阵;Γ1ΔYt-1+…+Γp-1ΔYt-(p-1)是p-1个滞后差分项,p即滞后长度;DX即漂移项和趋势项; ΔYt和滞后差分项都是平稳的,所以,ΠYt-1也必定是平稳的。而ΠYt-1是唯一包含一阶单整序列的项,所以如果Yt可以协整的话,ΠYt-1包含协整关系,Π矩阵的秩即为线性无关协整向量的个数。
然后执行迹检验或者最大特征值检验,得到长期均衡矩阵Π的秩的大小,同时也可以得到r个线性无关的协整向量。
3 EMI温度影响的协整消除方法
3.1 理论基础
在EMI方法中,电导频谱峰值频率即为结构固有频率[17],对于两端自由梁,第r阶固有频率的表达式为[18]
(4)
式中:E,L,A,I分别为梁的杨氏模量,长度,横截面积和惯性矩;ρ为梁的密度;αr只与模态阶数有关。 假设ωm,ωn,ωq分别为第m,n,q阶固有频率随温度变化的序列,则
(5)
即3个序列线性相关,比值仅与频率所在阶数有关,而与其他参数无关。对于矩阵ω=[ωm,ωn,ωq],其最大线性无关组只有一个向量,即r(ω)=1。对于线性方程组ωβ=0应当有3-1=2个线性无关解,即对于ωm,ωn,ωq这3个时间序列有2个线性无关的协整向量,由此,可以得到2个相应的协整方程,即
β11ωm+β12ωn+β13ωq=ε1
(6)
β21ωm+β22ωn+β23ωq=ε2
(7)
式中:β1=[β11,β12,β13],β2=[β21,β22,β23]是两个线性无关的协整向量;ε1~(0,σ2),ε2~(0,σ2), 且ε1,ε2相互独立。温度变化下的协整余量ε1,ε2是平稳的。温度变化时,结构的相关参数会产生连续有规律的变化,温度对阻抗谱的影响是整体的;而损伤发生时,结构的局部刚度和阻尼会发生变化,损伤对阻抗谱的影响是局部的。因此,在结构损伤后,峰值频率序列不再满足之前的协整关系,将相应频率序列代入式(6)和式(7)中,得到的余量ε1d,ε2d将与ε1,ε2有明显不同。
3.2 损伤识别过程
在EMI方法中,以电导谱峰值频率作为协整变量,首先建立温度变化工况下健康状态结构的电导谱峰值频率序列。利用ADF检验和Johansen检验确定其不平稳阶数,将温度变化影响下不平稳的阻抗谱峰值频率时间序列协整为一个平稳的余量序列,有效消除了环境温度影响。结构损伤发生时,平稳的协整余量序列发生突变,准确表征了结构损伤的发生。
4 实验及结果分析
4.1 实验装置及试件
利用压电片高频主动激励进行钢板在温度变化工况下模拟损伤的EMI检测实验。
实验试件为700×90×3 mm3的430钢板, 一个PZT传感器(直径12 mm,厚度0.6 mm,STEMINC SMD 12T06R412WL),改性丙烯酸酯胶,一个钕铁硼磁铁(重2.69 g)。利用改性丙烯酸酯胶将PZT粘贴在钢板指定位置,将磁铁吸附在钢板上作为损伤,如图1所示,吸附磁铁后,结构机械阻抗发生变化,并且不会造成永久性损伤,可以进行重复实验。

图1 实验试件及位置图(mm)Fig.1 Experimental specimen and location map(mm)
图2所示为自制阻抗测量系统,该系统可以代替通用阻抗仪测量结构阻抗谱,且能够实现对结构的连续监测。该阻抗测量系统包括自传感电路与数据采集分析系统两部分,其中自传感电路由PZT传感元件、电阻/电容元件及连接线构建,数据采集分析部分则由NI数据采集系统组成,如图3所示。NI数据采集系统型号为NI PXIe-1071,采用PXIe-6124采集卡。系统软件通过LabVIEW编程开发,借助NI-DAQmx提供的硬件驱动接口,可以方便地对采集卡的输出与采集功能进行控制编程。

图2 阻抗测量系统Fig.2 Impedance measurement system
首先,通过NI数据采集系统对PZT传感器施加电压激励Vi,激励信号为与所需测量阻抗信号点频率相同单一频率正弦信号。由数据采集系统采集自传感线路中的电容或电阻的电压信号V0。最后,计算所测结构单频率点的阻抗值。若自传感电路中采用电阻元件,阻抗计算公式为
(8)


(9)
式中: j为虚数单位;ω为激励信号频率;C为电容元件电容值。改变激励信号频率,利用LabVIEW程序编程的循环结构,重复以上过程即可得到不同频率点的阻抗值,从而得到结构阻抗谱。LabVIEW编程时,利用定时功能即可实现对结构阻抗信息的定时采集。
实验使用高低温交变实验箱(LRHS-504B-LJ)使试件处于温度变化工况下,如图4所示。
4.2 实验方案
将钢板放在温度箱内,两端自由,如图5所示。使钢板所处环境温度从-15~115 ℃反复连续变化,利用NI系统每10 s测一次钢板的电导频谱,频率范围选择为53~57 kHz,利用MATLAB提取电导频谱54.8~55.2 kHz,55.3~55.7 kHz,56.4~56.8 kHz频率段内的3个共振峰明显的峰值频率时间序列,即结构的3个固有频率时间序列,获得结构正常时的参考数据,对其进行ADF检验和协整检验,得到协整方程和协整余量;110 min后,将磁铁放置在图1中所示位置模拟损伤发生,其余条件不变,仍然利用NI系统每10 s测得一次钢板的电导频谱,得到钢板在损伤情况下相应的3个峰值频率时间序列,代入上一步求得的协整方程中,得到相应的的协整余量并对其进行分析。

图3 NI阻抗采集分析系统Fig.3 NI impedance acquisition and analysissystem

图4 温度箱Fig.4 Temperature box

图5 温度箱内部试件状态Fig.5 The specimen status in temperature box
选择扫描频率范围时,必须包含试件的固有频率,对于金属材料,其高阶固有频率一般在30~100 kHz,试验时先将频带选为30~100 kHz,然后选出波形较好,共振峰明显的53~57 kHz频带范围。该频段虽然相对较窄,但是包含若干个峰值频率,已经达到了协整处理的数据需求;且频带相对较窄会使得电导频谱峰值频率精度较高,实验数据更加精确。
4.3 实验结果及其分析
4.3.1 温度对电导频谱的影响
图6所示是在20 ℃和40 ℃下的电导频谱。通过实验可以发现,当温度升高时,电导频谱向左移动,峰值频率减小,幅值增大,但频谱形状几乎不变。图7是20 ℃时试件在正常和损伤状态下的电导频谱。损伤发生时,电导频谱形状变化,产生频移和幅值变化,变化规律与温度有所不同,但两者不易区分。
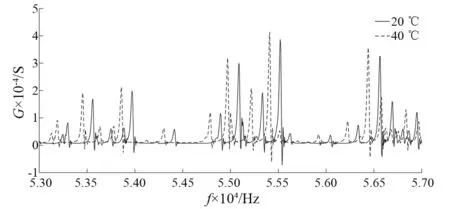
图6 20 ℃和40 ℃的电导频谱Fig.6 Conductance signatures at 20 ℃ and 40 ℃

图7 20 ℃正常和损伤时的电导频谱Fig.7 Normal and damaged conductance signatures at 20 ℃
以0 ℃结构正常时的电导频谱作为参考数据,各种情况下的均方根值(RMSD)如表1所示。以正常结构在20 ℃时的RMSD为参考点,温度和损伤均会对RMSD的值产生影响,甚至温度对RMSD的影响比损伤还要大。也就是说,温度变化会对损伤识别产生影响,甚至会淹没损伤的影响。

表1 各种情况下的RMSD表
4.3.2 温度对电导频谱谐振峰值的影响
图8所示是从电导频谱中提取的54.8~55.2 kHz频率段内(图7虚线处)峰值频率随温度的变化,两者呈线性关系。图9所示是实验获取的3个峰值频率时间序列,3个序列变化趋势相同,满足协整的其中一个前提条件。

图8 不同温度下的某阶共振频率值Fig.8 The peak frequency at different temperatures

图9 3个峰值频率时间序列Fig.9 Three peak frequency time series
4.3.3 协整结果及分析
首先,对上述3个时间序列执行ADF检验,建立各自的VAR模型,计算t统计量的值,进行显著性检验,判断序列为非平稳时间序列,对序列作一阶差分,执行上述相同步骤,序列仍为非平稳的,再作二阶差分,序列是平稳的,故3个峰值频率序列均为二阶非平稳时间序列。3个序列变化趋势相同,不平稳阶数相同,符合协整条件。
然后,执行Johansen检验,建立误差修正模型,即式(3),利用最大似然法估计矩阵Π的秩为r=2, 即有2个线性无关的协整向量。 将Π分解为Π=ABT, 其中,A,B均为n×r矩阵(n为序列个数), 并且r(A)=r(B)=r,B的r列即为r个线性无关的协整向量,协整向量即协整方程系数,于是得到2个协整式(10)和式(11)。
u1=0.501 9ω1+0.121 3ω2-0.599 1ω3-500.1
(10)
u2=0.388 4ω1-0.637 7ω2+0.207 7ω3+2 268.3
(11)
式中:u1,u2为2个协整余量序列;ω1,ω2,ω3为实验中获取的3个峰值频率序列。此时,2个余量序列均是平稳的。
假设余量序列服从标准正态分布,利用3σ准则确定余量序列的上下控制限。中心线为余量序列均值,上下限分别为
UCL=CL+3σ
(12)
LCL=CL-3σ
(13)
式中:CL为余量序列均值;σ为余量序列标准差。对于新的待检数据,分别将其代入协整式(10)和式(11)中,得到相应的协整余量。若余量仍在控制限内,说明结构没有损伤,反之,则判断为结构产生损伤。
最后,将钢板在损伤情况下相应的3个峰值频率序列代入协整式(10)和式(11)中,此时,协整余量序列发生突变,均在控制限外,且损伤后的余量序列不再平稳,如图10所示,虚线代表损伤发生。
图10中,损伤发生前余量序列平稳,说明协整方法有效消除了温度影响,损伤发生时,余量突变,超出控制限,且序列不再平稳,表征损伤发生的现象明显。这是由于温度与损伤对峰值频率的影响机制与规律不同,温度对阻抗谱的影响是整体的,温度变化时,结构的相关参数会产生连续有规律的变化,从而使得阻抗谱产生左右偏移和幅值变化,而阻抗谱形状几乎不改变;损伤对阻抗谱的影响是局部的,损伤发生时,结构的局部刚度和阻尼会发生变化,从而使阻抗谱产生偏移、幅值变化、峰值分裂、峰值合并、峰值消失、产生新的峰值等,阻抗谱形状显著改变,这不同于温度的影响。因此,峰值序列间的线性组合可以消除温度影响,但不会消除损伤影响。由此,验证了在EMI方法中利用协同整合思想消除温度影响的有效性。
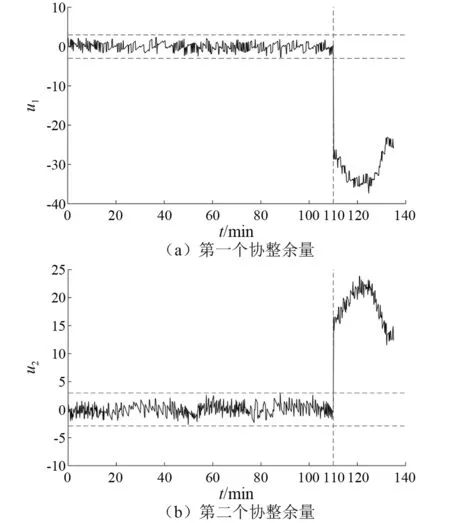
图10 2个协整余量序列Fig.10 Two cointegration residuals
对正常情况下得到的2个余量序列u1和u2作ADF检验, 检验结果表明u1序列比u2序列更加平稳,并且根据图10可以知道,损伤发生时,u1突变的幅度更大,对损伤更加敏感。以u1作为新的损伤特征量效果更好。
5 结 论
本文基于协整处理阻抗谱以消除温度影响,通过钢板在温度变化工况下模拟损伤的EMI检测实验,发现温度升高时,电导谱向左移动,峰值频率减小,幅值增大;电导谱峰值频率与温度呈线性关系。本文基于实验选取的3个在温度影响下不平稳的峰值频率时间序列,有2个线性无关的协整向量,从而得到2个平稳的协整余量,且第一个协整余量更加平稳。损伤发生后,2个余量序列均发生突变,且损伤时的余量序列不再平稳,验证了阻抗谱协整处理环境温度变化方法的有效性,且第一个余量序列对损伤更加敏感。在长期监测中,基于协整处理阻抗谱以消除温度影响,不必研究损伤指标与温度的具体关系,不必记录环境温度值,且对微小损伤敏感,表征结构损伤的效果明显,相对于其他方法有明显优势,在实际应用中有很大参考价值。
