一维六方压电准晶中圆孔边周期裂纹分析

杨 娟, 李 星， 周跃亭

(1.宁夏大学 民族预科教育学院，银川 750002；2.宁夏大学 数学统计学院，银川 750021；3.同济大学 航空航天与力学学院，上海 200092 )

1984年准晶体的发现是近年来凝聚态物理的一大突破。准晶作为一类新型材料，与传统材料相比，由于其独特的准周期结构，表现出与众不同的一些性能，在众多科学技术领域有广泛的应用前景。由于准晶中相位子场的存在,导致准晶压电性能比传统晶体要复杂得多。目前，含缺陷准晶材料的断裂问题研究已取得了大量的重要成果[1-4]。压电准晶材料是一种特殊的压电材料,正是由于准晶材料具有压电效应这种特殊性能，与一般的压电材料相比,允许有五次或高于六次的旋转对称操作。所以, 压电准晶材料比普通的压电材料有着良好的应用前景。对于压电效应下的准晶断裂问题在近几年才有研究，目前压电准晶材料的方程已经初步建立[5],文献[6]指出,三维准晶和部分拥有中心对称的二维准晶是没有压电效应的,因此研究主要放在了一维压电准晶材料上。在实际的工程应用中，材料破坏的形式多种多样，实际的结构也千变万化。一般而言，材料开孔现象非常常见，比如机械结构中的螺栓孔，飞机蒙皮中的铆钉孔等。在复杂的加载环境下，含孔洞的结构不可避免的会出现应力集中，在孔边诱发裂纹，从而导致材料的断裂破坏。因此，研究孔边裂纹问题具有重要的理论意义和工程价值。文献[7]采用Green函数法研究界面上含圆孔边界径向有限长度裂纹的两半无限压电材料对SH波的散射和裂纹尖端动应力强度因子问题。文献[8]采用“镜像”和“剖分-契合”等方法,对SH波作用下半空间孔边界面裂纹的动应力问题进行了研究。文献[9]采用 Green 函数法对压电材料中多个孔边径向裂纹的相互作用问题进行了研究。文献[10]采用数字激光动态焦散线实验系统，研究爆炸荷载作用下空孔缺陷对裂纹扩展行为的作用关系，以及裂纹扩展行为的规律。

近几年,关于一维压电准晶材料弹性与断裂力学研究成果已经涌现了不少[11-20]。从上述文献中可以看出，涉及准晶材料断裂力学研究问题时，缺乏数值算例。因为只有通过数值分析， 解决准晶材料本质的物理问题，比如声子-相位子场的耦合、电场耦合、相位子场的出现对裂纹的影响等等，这样才对研究准晶材料有意义，并有别于其他的材料。论文作者曾借助于保角映射在渗透型边界条件和非渗透型边界条件下研究了一维六方准晶中圆孔边单裂纹和三条不对称裂纹的电弹问题，通过数值分析探讨了裂纹长度、半径、耦合系数、声子场载荷、以及相位子场载荷和电载荷对应力强度因子和电位移强度因子的影响[21-22]，在此基础上，Yang等[23]考虑部分渗透电边界条件，基于Stroh公式，研究了压电效应下一维六方准晶材料中具有不对称共线裂纹的椭圆孔边反平面断裂问题，给出裂纹尖端场强度因子和能量释放率的解析表达式，通过数值算例分析了几何参数、耦合系数、以及相位子场载荷和机电载荷对材料断裂特性的影响规律。但值得注意的是，上述工作论文作者仅是针对圆孔边单裂纹和三条不对称裂纹以及不对称共线裂纹的椭圆孔边情况。而实际工程中多个裂纹的模型是普遍存在的，再者材料科学家和工程师们已经开始通过微结构工程设计、研制各种复合材料，在计算机辅助复合材料设计中，通常设计具有周期分布微结构的材料，而且现代材料制造技术已有能力实现精确周期分布。同时在研究大量缺陷相互作用时，将缺陷抽象为周期有序排列是一个实用、有效的力学模型。因此，对于周期型裂纹模型的研究也是有重要的实际工程意义的。除此之外，据论文作者所知，并无其他文献对一维六方压电准晶中圆孔边周期裂纹问题进行过研究。

本文借助于力学和应用数学模型，运用复变函数方法和解析函数理论，对一维六方压电准晶中圆孔边周期裂纹反平面断裂问题进行了分析研究。获得电不可导通边界条件和电可导通边界条件下裂纹尖端应力强度因子，电位移强度因子和能量释放率。通过数值算例分析裂纹数、几何参数、耦合参数、声子场应力、相位子场应力和电载荷对材料断裂特性的影响规律。

1 一维六方压电准晶基本理论

由文献[24]知，对于其准周期方向为沿x3轴并且周期平面为(x1,x2)面的一维六方压电准晶体的反平面弹性问题的最终控制方程为

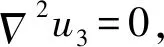
(1)

式中：u3和v分别为声子场和相位子场的位移；φ为电势。由复变函数理论可知[25]，u3,v和φ可表示为三个解析函数的实部或虚部，不妨设

u3=Reφ1(z),v=Reφ2(z),φ=Reφ3(z)

(2)

式中：φi(z)(i=1,2,3)为任意三个解析函数。所以一维六方压电准晶的弹性平衡问题最终归结为在适当边界条件下求解式(2)。为了简便，下文中都有φi来表示φi(z)。

2 一维六方压电准晶中圆孔边周期裂纹问题的解析解

2.1 力学模型

如图1所示，在一维六方压电准晶体中含一半径为R的圆孔，沿孔壁均匀分布着k(k=1,2,3，…)个长度为L的周期径向裂纹。假设x3轴方向为准周期方向，且裂纹穿透准周期方向，垂直于准周期方向的平面为坐标平面x1-x2。准晶体在无穷远处受沿声子场与相位子场边界的纵向剪应力以及面内电载荷的作用。

图1 一维六方压电准晶中具有个周期裂纹的圆孔边(An的坐标为n=0,1,2,…,k-1)Fig.1 k periodic radial cracks emanating from a circular hole in 1D hexagonal piezoelectric quasicrystalsn=0,1,2,…,k-1)

2.2 场强度因子

2.2.1 电不可导通边界条件

线弹性理论表明，仅对应力集中而言，此问题可以转化为在无穷远处不受外应力，仅在圆孔边及其所带裂纹的表面上受纵向剪切力和电载荷作用σ32=-τ1,H2=-τ2,D2=-D0，并考虑电不可导通边界条件, 则该问题的电力学边界条件可表示为

(3)

式中：N为具有k(k=1,2,3,…)个周期径向裂纹的圆孔边的边界；σ32和H2分别为声子场和相位子场;D2为电位移。

对于电不可导通边界条件， 有

(4)

将边界条件式(3)代入式(4)，可得

(5)

引入保角变换[26]

(6)

对式(6)两端关于ζ求导，得

(7)

这里有

(8)

从式(7)，可得

(9)

其中，

A=-8(1+ε)e4nπi[-3+ε+(1+ε)cos(2nπ)]sin2(nπ);

[2ki(ε-1)cos(nπ)+(ε-7)sin(nπ)+(1+ε)sin(3nπ)]。又由式(8)有

(10)

(11)

式中：K为无量纲场强度因子，其表达式为

(12)

特别地，当n=0时,有式(12)得电不可导通边界条件下一维六方压电准晶中圆孔边k个周期裂纹在(A0,0,0)处声子场与相位子场应力强度因子及电位移强度因子分别为

(13)

式中：K*为无量纲场强度因子，为

(14)

2.2.2 电可导通边界条件

考虑电可导通裂纹，则边界条件为

(x1,x2)∈N∶σ32=-τ1,H32=-τ2,φ=C(常数)

(15)

对于电可导通边界条件， 有

(16)

所有的应力与电位移均由φi(i=1,2,3)表示, 只要解出φi, 便可以确定应力场和电位移场。

将边界条件式(15)代入式(16)，可得

(17)

在电可导通边界条件下，由Fan的研究得一维六方压电准晶中圆孔边k个周期裂纹在(An,0,0)(n=0,1,2,…,k-1)处声子场与相位子场应力强度因子及电位移强度因子分别为

(18)

特别地，当n=0时,有式(18)得电可导通边界条件下一维六方压电准晶中圆孔边k个周期裂纹在(A0,0,0)处声子场与相位子场应力强度因子及电位移强度因子分别为

(19)

2.3 能量释放率

当不考虑电载荷作用时，由式(13)得一维六方弹性准晶中圆孔边k个周期裂纹在(A0，0，0)处声子场和相位子场应力强度因子分别为

(20)

此时，一维六方弹性准晶中圆孔边k个周期裂纹在(A0,0,0)处的能量释放率为

(21)

当不考虑相位子场作用时，由式(13)和式(19)分别得到在电不可导通和电可导通边界条件下各向同性压电材料中圆孔边k个周期裂纹在(A0,0,0)处应力强度因子和电位移强度因子分别为与文献[28]中的结果完全一致。此时，在电不可导通和电可导通边界条件下，各向同性压电材料中圆孔边k个周期裂纹在(A0,0,0)处能量释放率分别为

(22)

(23)

(24)

(25)

2.4 结果与讨论

(1) 当k=1时，由式(13)和式(19)分别得

(26)

(27)

式(26)和式(27)分别是电不可导通和电可导通边界条件下一维六方压电准晶中圆孔边单裂纹在处的场强度因子，与Yang等研究的结果完全一致。

(2)当k=2时，由式(13)和式(19)分别得

(28)

(29)

式(28)和式(29)分别是电不可导通和电可导通边界条件下一维六方压电准晶中圆孔边对称共线裂纹在(A0,0,0)处的场强度因子。

(3)当k=3时,由式(13)和式(19)分别得

(30)

(31)

式中：K**为无量纲场强度因子，其表达式为

(32)

特别地，当不考虑电场作用时，一维六方弹性准晶中圆孔边均匀分布的三个径向裂纹在(A0,0,0)处能量释放率为

(33)

当不考虑相位子场作用时，在电不可导通和电可导通边界条件下，各向同性压电材料中圆孔边均匀分布的三个径向裂纹在(A0,0,0)处能量释放率分别为

(34)

(35)

(4)当k=4时,由式(13)和式(19)分别得

(36)

(37)

式(36)和式(37)分别是电不可导通和电可导通边界条件下一维六方压电准晶中圆孔边对称共线四裂纹在(A0,0,0)处的场强度因子。

(5)当R→0时，由式(13)和式(19)分别得

(38)

(39)

式中:K***为无量纲场强度因子，其表达式为

(40)

式(38)和式(39)分别是电不可导通和电可导通边界条件下一维六方压电准晶中星形裂纹(即k个共点的周期裂纹)在(A0,0,0)处的场强度因子。仅考虑声子场，式(40)所得结果与文献[29]一致。

特别地，当不考虑电场作用时，一维六方弹性准晶中星形裂纹在(A0,0,0)处能量释放率为

(41)

当缺失相位子场时，在电不可导通和电可导通边界条件下，各向同性压电材料中星形裂纹在(A0,0,0)处能量释放率分别为

(42)

(43)

3 数值算例和分析

图2显示了在不同的裂纹长度L/R下，无量纲场强度因子K*随裂纹数k的变化关系。k=3时对应的无量纲场强度因子是最大的，k=2,4时对应的无量纲场强度因子相等，且大于k=1时对应的无量纲场强度因子。这就说明，圆孔边均匀分布三裂纹的材料最危险；含圆孔边对称共线裂纹或对称四裂纹的材料比含圆孔边单裂纹的材料危险。另外，当k>5时对应的无量纲场强度因子小于k=1所对应的无量纲场强度因子。还可以看出，随着裂纹数量(k≥3)的增加，无量纲场强度因子进一步减小。说明，在材料中包含具有多个裂纹(k≥3)的圆孔, 增加裂纹的数量可以提高这种材料的可靠性。特别，裂纹的数量趋于无穷时，无量纲场强度因子趋于零，这是因为具有多条裂纹圆孔的边界被认为是一个新的圆孔，并且大于原来的圆孔。此外，L/R越大，K*也越大。

图2 对不同L/R,K*随k的变化(圆孔边周期裂纹)Fig.2 Variations of K* with k for different L/R

图3给出了k=1,2,3,4时，无量纲场强度因子K*随裂纹长度L/R的变化关系(R=0.05)。随着裂纹长度的增加，无量纲场强度因子逐渐增大，并且最终趋于某个常数。另外，在裂纹长度一定的情况下，k=3时对应的无量纲场强度因子最大，k=2,4时对应的无量纲场强度因子相等，且大于k=1时对应的无量纲场强度因子,与图2中得到的结论一致。

图3 对k=1,2,3,4,K*随L/R的变化(圆孔边周期裂纹)Fig.3 Variations of K* with k for k=1,2,3,4

图4给出了k=1,2,3,4时,无量纲场强度因子K*随半径R的变化关系(L/R=0.05)。随着半径的增加，无量纲场强度因子逐渐增大。并且在半径大小一定的情况下，k=3时对应的无量纲场强度因子最大，k=2,4时对应的无量纲场强度因子相等，且大于k=1时对应的无量纲场强度因子，与图2中得到的数值结果一致。

图5给出了在不同半径R下，无量纲场强度因子K**随裂纹长度L/R的变化关系。当半径大小固定时，无量纲场强度因子随裂纹长度的增大而增大，但增加越来越缓慢。此外，半径越大，无量纲场强度因子也越大，这表明，通过调整圆半径可以消除裂纹尖端附近的应力集中。

图4 对k=1,2,3,4,K*随R的变化(圆孔边周期裂纹)Fig.4 Variations of K* with R for k=1,2,3,4

图5 对不同R,K**随L/R的变化(圆孔边均布三裂纹)Fig.5 Variations of K** with L/R for different R

图6给出了在不同的裂纹长度L下，裂纹数k对无量纲场强度因子K***的变化关系。k=3时对应的无量纲场强度因子最大，k=2,4时对应的无量纲场强度因子相等，且大于k=1时对应的无量纲场强度因子。这就说明，具有共点的均匀分布三裂纹的材料最危险；具有共点的对称共线裂纹或对称四裂纹的材料比具有单裂纹的材料危险。另外，当k>13时所对应无量纲场强度因子小于k=1所对应的无量纲场强度因子。还可以看出，随着裂纹数(k≥3)的增加，无量纲场强度因子进一步减小。说明，在材料中包含具有多个共点的裂纹(k>3), 增加裂纹的数量可以提高这种材料的可靠性。特别，裂纹数趋于无穷时，无量纲场强度因子趋于零。此外，L越大，K***也越大。

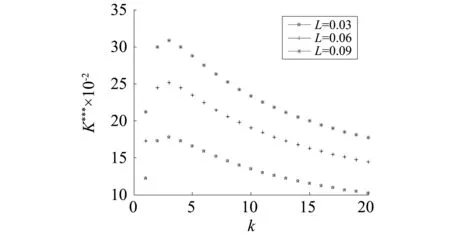
图6 对不同L,K***随k的变化(星形裂纹)Fig.6 Variations of K*** with k for different L

图7给出了在声子场和相位子场共同作用下，不同的耦合系数R3对能量释放率G/Gr随裂纹数k的变化曲线。从图中可以看出，耦合系数R3越大，能量释放率也越大，但随着裂纹数的不断增加，耦合系数对能量释放率的影响越来越小。所以，在工程实际中通过调整耦合系数可以降低裂纹尖端的集中。

图7 对不同R3,G/Gr随k的变化(圆孔边周期裂纹)Fig.7 Variations of G/Grwith k for different R3

图8显示了在不同的声子场和相位子场作用下，不同的裂纹长度L/R对能量释放率G/Gr随裂纹数k的变化曲线。从图可以看到，相位子场应力τ2越大，能量释放率也越大。结果表明,在给定的声子场载荷下，相位子场载荷总是促进裂纹扩展。另外，裂纹长度越大，能量释放率也越大。结果显示，裂纹长度变得越长越容易造成材料破坏，因此在实际应用中可以通过检测裂纹长度的变化来预防因为裂纹扩展而造成的工件失效。

图8 对不同τ2和L/R,G/Gr随k变化(圆孔边周期裂纹)Fig.8 Variations of G/Grwith k for different τ2

从图7和图8中可以注意到，裂纹数对能量释放率的影响规律情形与图2中裂纹数对无量纲场强度因子的影响规律情形相似。

图9和图10分别给出了不同的耦合系数R3对能量释放率G/Gr随裂纹长度L/R和相位子场载荷τ2的变化关系。从图9和图10可以看出, 耦合系数R3越大，能量释放率G/Gr也越大。另外，能量释放率随着裂纹长度的增大而增大，随着相位子场载荷的的增大也增大。因此适当调节相位子场载荷可以抑制材料的性质变化和裂纹扩展。

图9 对不同R3,G/Gr随L/R变化(圆孔边均布三裂纹)Fig.9 Variations of G/Gr with L/R for different R3

图10 对不同R3,G/Gr随τ2变化(圆孔边均布三裂纹)Fig.10 Variations of G/Gr with τ2 for different R3

图11给出了在不同的声子场和相位子场作用下，能量释放率G/Gr随半径R的变化关系。从图中可以看出，能量释放率随着半径的增大而呈线性增加。但声子场载荷τ1越大，能量释放率反而越小，但总的来看声子场载荷对能量释放率的影响很小，因此在实际工程中可以适当控制声子场载荷有利于提高材料的抗断裂能力。

图11 对不同τ1,G/Gr随R变化(圆孔边均布三裂纹)Fig.11 Variations of G/Gr with R for different τ1

图12给出了在声子场和相位子场共同作用下，不同的耦合系数R3对能量释放率G/Gr随裂纹数k的变化曲线。从图12中可以看出，耦合系数越大，能量释放率也越大。但随着裂纹数的不断增加，耦合系数对能量释放率的影响越来越小。所以，在工程实际中通过调整耦合系数可以降低裂纹尖端的集中。

图12 对不同R3,G/Gr随k变化(星形裂纹)Fig.12 Variations of G/Gr with k for different R3

图13显示了在不同的声子场和相位子场作用下，不同的裂纹长度L对能量释放率G/Gr随裂纹数k的变化曲线。从图中可以注意到，相位子场应力τ2越大，能量释放率也越大。另外，裂纹长度越大，能量释放率也越大。但随着裂纹数的不断增加，相位子场和裂纹长度对能量释放率的影响都越来越小。

从图12和图13中可以注意到，裂纹数对能量释放率的影响趋势与图6中裂纹数对无量纲场强度因子的影响趋势相似。

图14给出了压电陶瓷(PZT-4)在电不可导通和电可导通边界条件下，能量释放率G/Gr随裂纹数k的变化关系(τ1=2 MPa,D0=6×10-3C/m2,R=0.01,L/R=0.005)。从图14中可以看出，裂纹数在两种边界条件下对能量释放率的影响规律情形相似，且能量释放率随裂纹数的变化趋势与图2中无量纲场强度因子随裂纹数量的变化趋势相似。

图14 G/Gr随k的变化(圆孔边周期裂纹)Fig.14 Variations of G/Grwith k

图15给出了压电陶瓷(PZT-4)在电不可导通和电可导通边界条件下，能量释放率G/Gr随半径R的变化关系(τ1=6 MPa,D0=2×10-3C/m2,L/R=0.05)。从图15中可以看出，半径在两种边界条件下对能量释放率的影响规律情形相似。即能量释放率随着半径的增加而正比例增加，表明半径总是促进裂纹增长。

图15 G/Gr随R的变化(圆孔边均布三裂纹)Fig.15 Variations of G/Grwith R

图16给出了压电陶瓷(PZT-4)在电不可导通和电可导通边界条件下，在力电载荷给定下能量释放率G/Gr随裂纹长度L/R的变化关系(τ1=6 MPa,D0=2×10-3C/m2,R=0.05)。可以看出，裂纹长度在两种边界条件下对能量释放率的影响规律情形相似，即随着裂纹长度的增加，能量释放率在增加，表明裂纹长度的增加容易促进裂纹扩展。

图16 G/Gr随L/R的变化(圆孔边均布三裂纹)Fig.16 Variations of G/Gr with L/R

图17给出了压电陶瓷(PZT-4)在电不可导通和电可导通边界条件下，能量释放率G/Gr随机械载荷τ1的变化关系(R=0.01,L/R=0.005,D0=2×10-3C/m2)。可见，机械载荷在两种边界条件下对能量释放率的影响规律情形相似。当裂纹的几何参数固定时，在一定的电载荷下，能量释放率随机械载荷的增加而增加。说明，机械载荷始终促进裂纹的扩展。

图17 G/Gr随τ1的变化(圆孔边均布三裂纹)Fig.17 Variations of G/Grwith τ1

图18给出了压电陶瓷(PZT-4)在电不可导通和电可导通边界条件下，能量释放率G/Gr随电载荷D0的变化关系(R=0.01,L/R=0.005,τ1=6 MPa)。从图中可以看出，在电可导通边界条件下，电载荷对能量释放率没有影响，裂纹的能量释放率仅依赖于机械载荷。在电不可导通边界条件下，当裂纹的几何参数固定时，在一定的机械载荷下，能量释放率随着负电场量值大小的增加而减少。相比之下，随着正电场从零开始增加，能量释放率逐渐增加，并在D0≈2.2×10-3C/m2时达到高峰，然后随着正电场的进一步增加，能量释放率不断减小。结果表明,对于电不可导通裂纹,在给定的机械载荷下，负电场总是阻碍裂纹扩展，而正的电场可以促进或阻滞裂纹扩展，这取决于电载荷的大小、方向和作用方式。

图18 G/Gr随D0的变化(圆孔边均布三裂纹) Fig.18 Variations of G/Grwith D0

图19给出了压电陶瓷(PZT-4)在电不可导通和电可导通边界条件下，能量释放率G/Gr随裂纹数k的变化关系(τ1=2 MPa,D0=6×10-3C/m2,L=0.005)。从图中可以看出，裂纹数在两种边界条件下对能量释放率的影响规律情形相似，且能量释放率随裂纹数的变化趋势与图3中无量纲场强度随裂纹数量的变化趋势相似。

图19 G/Gr随k的变化(星性裂纹)Fig.19 Variations of G/Grwith k

从图14～图19中还可以看出，电可导通边界条件下能量释放率的值比电不可导通边界条件下能量释放率的值略大一些。

上述算例中得到的数值结果与Guo等研究中的数值结果相吻合。

4 结 论

本文运用复变函数方法和解析函数理论，对一维六方压电准晶中圆孔边周期裂纹反平面断裂问题进行了分析研究，导出了电不可导通边界条件和电可导通边界条件下裂纹尖端场强度因子和能量释放率的解析表达式。在缺失相位子场或电场时，所得结果和已有结果做了对比分析。通过数值算例分析了裂纹数、几何参数、耦合参数、以及相位子场载荷和机电载荷对材料断裂特性的影响规律。本研究为压电准晶元件的优化设计和可靠性分析提供理论基础，并丰富该领域断裂力学的研究内容。