非线性包装系统中关键部件振动可靠度分析

朱大鹏

(兰州交通大学 交通运输学院，兰州 730070)

包装件在流通过程中，在外界各种载荷作用下，产品或产品中关键部件的加速度响应会超出脆值而发生损坏。由于在流通中，产品的跌落冲击会在短时间内造成产品运动状态较大的改变，很容易造成产品的损坏，因此国内外研究者针对包装件在跌落冲击条件下中的问题开展了一系列研究。

王军等[1-3]将包装件建模为二自由度非线性系统，将跌落冲击等效为半正弦激励，采用数值分析的方法研究了包装件关键部件的响应，分析各参数对响应的影响，提出了三维冲击谱的概念。Zhong等[4]考虑了包装件中的干摩擦，对包装件传统等效跌落理论进行了改进。Zhong等[5]对我国快递行业中包装件流通环境进行了测试，重点调查了包装件的跌落高度和跌落姿态。Gibert等[6]构建了泡沫缓冲材料在跌落冲击条件下的一种新模型，该模型能准确模拟包装件的响应，应用该模型可准确获得材料的缓冲曲线。Piatkowski等[7]提出了一种应用泡沫材料的缓冲曲线确定材料在产品跌落过程中受到的应力和应变的情况。文献[8-9]分析了包装件受到跌落冲击时的响应，获得了产品的破损边界曲线，分析了参数对边界曲线的影响。郝蒙等[10]将包装件中的关键部件建模为集中质量的悬臂梁，分析包装件在跌落过程中易损件响应及各参数对响应的影响。卢富德等[11-12]将包装件中易损部件建模为简支梁和杆式结构，应用差分法分析易损件在跌落过程中的响应情况。在综述文献[13]中，作者从冲击机理、冲击动力学、试验方法、模拟方法等角度对国内外包装件跌落冲击的现状和发展趋势进行了介绍。

以上的研究对确保包装件的安全提供了理论基础、设计依据和试验方法。包装件在流通过程中，除了跌落冲击外，在大部分时间内受到的载荷是随机振动。在随机振动载荷作用下，包装件中的产品关键部件响应可能会超出脆值而造成产品损坏，这种现象称为产品的首次穿越损坏，首次穿越损坏是产品在流通过程中的一种重要损坏方式。分析包装件在流通过程中首次穿越失效概率，分析参数变化对失效概率的影响，对于优化包装设计，提高包装件振动可靠度，提高包装件在流通过程中的安全性具有重要意义。目前，关于包装件振动可靠度分析的文献较少，文献[14-15]分别介绍了单自由度包装件的位移响应和加速度响应首次穿越失效概率的分析方法。本文在朱大鹏等研究的基础上考虑了包装系统中的关键部件，考虑了包装件流通过程中真实随机振动激励的功率谱密度特征，构建了包装件失效概率分析方法，分析结构参数变化对失效概率的影响。本文的研究对于分析非线性包装件在流通过程中的可靠度，优化包装结构，降低包装件中关键部件损坏概率，具有重要的理论指导意义。

1 真实随机振动在标准正态空间中的表示

(1)

图1中实线表示的是实测的铁路运输过程中兰州-呼和浩特棚车中的加速度PSD(Power Spectral Density)曲线图，从图中看出，包装件在铁路运输过程中受到的加速度激励的PSD曲线具有明显的多峰值特征，本文应用多阶Kanai-Tajimi模型表示图1所示的真实随机振动的PSD曲线[18]

(2)

式中：n为PSD曲线上峰值的个数；Gk，ωk，ζk分别为各单阶Kanai-Tajimi模型的谱强度、固有频率和阻尼比。图中，g=9.8 m/s2。从图1可以确定n=3，本文采用谱矩法[19]识别模型式(1)中的参数。对于单阶Kanai-Tajimi模型

(3)

定义谱矩为

(4)

式中：l为谱矩的阶次；ωu为功率谱G(ω)的截止频率。定义

图1 实测和模拟的铁路棚车加速度PSD曲线Fig.1 Real and simulated acceleration PSD curve in railway boxcar

式(3)中G0(ω)的1～3阶谱矩分别为

(5)

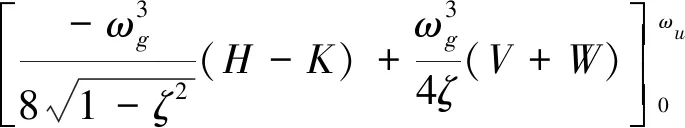
(6)

(7)

当n≥4时

(8)

根据式(3)中Gk(ω)和G0(ω)的关系， 可推导出Gk(ω)的i阶谱矩λki与G0(ω)的i阶谱矩λi具有关系

(9)

对于多阶Kanai-Tajimi模型式(2)，模型中参数识别步骤如下：

步骤1根据实测的PSD曲线，根据曲线上主要峰值的个数，确定模型式(2)中的n；

步骤2根据式(4)计算PSD曲线的3(n-1)+1，3(n-1)+2，3(n-1)+3阶谱矩，根据单阶Kanai-Tajimi模型中各参数识别方法，识别模型(2)中的G1，ω1，ζ1；

步骤3利用G1，ω1，ζ1计算该参数对应的单阶Kanai-Tajimi模型，计算实测PSD曲线和该单阶模型的差值，计算该差值曲线的3(n-2)+1，3(n-2)+2，3(n-2)+3阶谱矩，并识别出参数G2，ω2，ζ2；

步骤4重复步骤2和步骤3，直至求出模型式(2)中所有参数。

图2 单阶Kanai-Tajimi模型中ζ和ωg的识别Fig.2 Identification method for ζ and ωg in Kanai-Tajimi model

可用模型式(2)模拟实测的铁路棚车中加速度激励PSD特性，利用以上步骤得到模型的参数如表1所示。

表1 识别的3阶Kanai-Tajimi模型参数

表中，g=9.8 m/s2。利用表1中参数拟合出的3阶Kanai-Tajimi模型的PSD曲线如图1中点划线所示，从图1中可看出，3阶Kanai-Tajimi模型可准确模拟实测的铁路棚车加速度PSD曲线。根据该模型，可认为包装件在铁路运输过程中所受到的随机振动是由3个高斯白噪声源分别通过3个单阶Kanai-Tajimi滤波器后叠加生成的，其物理意义如图3所示。

图3 铁路棚车随机振动的数字模拟Fig.3 Digital generation of random vibration in railway boxcar

依图3，铁路运输过程中的随机振动激励可表示为

(10)

式中：hfj(t)为第j个滤波器的单位脉冲响应函数；Wj(t)为第j个滤波器对应的输入白噪声。 若采样时间间隔Δt足够小，且考虑到标准正态向量u中任一分量ui=Wi/σ，则式(10)可改写为

(11)

(12)

式中：σj为对应的高斯白噪声的方差，由表1中的G值分别确定：σ2=πG/Δt。 各阶单位脉冲响应函数hfj由式(13)确定

(13)

式中： 参数ω和ζ由表1中数据确定。

2 线性包装件振动可靠度分析方法

本文考虑了包装件中的关键部件，将包装件建模为二自由度支座激励系统，如图4所示。

图4 二自由度包装件模型Fig.4 Two degree of freedom package model

(14)

分母Δ为

AFK：是英文Away From Keyboard的缩写，分别由英语“Away”、“From”、“Keyboard”的首字母组成，表示“不在电脑前”。

(15)

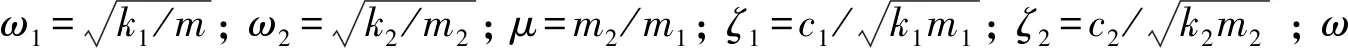
(16)

式中：L-1[·]为拉普拉斯反变换运算。

根据式(10)及式(16)，可得关键部件在t时刻的加速度响应表达式

(17)

式中： 向量a(t)=[a1(t),a2(t),…,an(t)]T，且

(18)

假定包装件的脆值为Gc，可定义包装件中关键部件的极限状态方程

g(u,Gc,t)=Gc-a(t)·u

(19)

很显然，如果方程g(u,Gc,t)>0，包装件安全，g(u,Gc,t)≤0， 则包装件发生首次穿越损坏。对于线性包装件，方程g(u,Gc,t)可用高维标准正态空间u中的超平面表示，如果包装件是非线性的，该极限状态方程是空间u中的一个超曲面。在空间u中定义极限状态方程上距离坐标原点最近的点为设计点u*

(20)

式中： ‖·‖为向量的模。

对于线性包装件，g(u,Gc,t)=0是一个关于u的线性方程， 故设计点可用式(21)求得

(21)

定义可靠度指标β为原点到设计点的距离

(22)

(23)

式中： 函数Ф[·]为标准正态累积分布函数。

3 非线性包装件等效线性化分析

对于线性包装件，可采用上述的方法分析在随机振动激励下关键部件的振动可靠度。通常包装件中缓冲材料是非线性的，由于非线性包装系统的响应不能用解析式表达，且非线性系统单位脉冲响应函数h(t)不存在，因此本文采用模型修正因子法[20]，用一个线性系统等效表示该非线性系统，再应用上述的方法分析包装件的振动可靠度。具体方法如下：

在标准正态向量空间u中，假定真实的非线性包装系统极限状态曲面由方程gr确定

(24)

构建一个理想化的线性包装系统极限状态曲面

(25)

则定义因子ν(u)为

(26)

根据ν(u)的定义，构建一个与真实系统等效的修正理想化系统

(27)

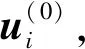
考虑到缓冲材料的非线性，假定缓冲材料的弹性具有三次非线性，则图4所示包装系统运动方程式为

(28)

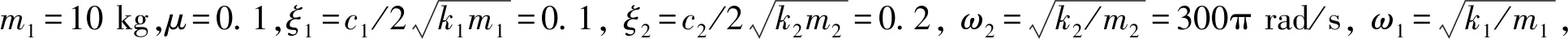
(29)

根据对朱大鹏的研究分析，应用模型修正因子法构建非线性包装系统的等效线性模型时，在迭代过程中，等效线性模型对应的可靠度指标βi与真实非线性系统可靠度指标β之间具有

β≤βi

(30)

这表明，‖β‖=min{‖βi‖}，因此，在构建等效线性系统时，可令ceq≈c，keq>k，则keq的求解是一个单目标最优化问题，即‖β‖达到最小时对应的keq即为所求。图5所示为应用模型修正因子法和式(30)计算出的keq和k1，α之间的关系，其中，ω1变化范围为100π～300π rad/s，α变化范围为104～30×104m-2，ceq可由给定的ξ1确定。从图5中可以看出，keq随着α的增加而增加，keq，α和k1基本上构成了一个平面。

图5 应用模型修正因子法确定的keq, α和k1曲面Fig.5 keq，α and k1 surface determined by use of model correction factor method

4 非线性包装件振动可靠度影响因素分析

以式(28)所表示的三次非线性包装件为例，分析各参数对振动可靠度的影响。假定脆值Gc=10g，其中，g=9.8 m/s2，k1eq和c1eq分别为采用模型修正因子法求出的非线性包装件的等效弹性系数和等效阻尼系数。在该条件下，采用式(23)分析包装件中关键部件首次穿越失效概率与时间的关系如图6所示。结果表明，与朱大鹏研究中的结果相似，二自由度包装系统中关键部件的损坏概率随时间的推移逐渐升高，最后达到稳定值。为验证模型修正因子法的准确性，图中给出了应用原始蒙特卡洛模拟(N=106)计算的包装件关键部件失效概率，对比结果表明，本文提出的二自由度包装系统关键部件损坏概率分析方法具有较好的准确性。

保持其他基本参数不变，分别改变参数ω2，ξ1eq，ξ2，μ，Gc的值，分析不同参数条件下，关键部件稳态损坏概率与ω1eq之间的关系，结果如图7所示。

图6 包装件中关键部件损坏概率分析结果Fig.6 Failure probability analysis results of critical component in packaging system

图7 参数变化对损坏概率的影响Fig.7 Effects of parameters varieties on failure probability

从图7的分析结果中可得以下基本结论：(1) 包装件关键部件首次穿越损坏概率与ω1eq相关，在ω1eq=500 rad/s～ω1eq=1 000 rad/s的范围内，失效概率明显增加，该峰值范围与真实随机振动PSD曲线的峰值频率范围相近。且在低于峰值频率时的损坏概率比高于峰值频率时的损坏概率低得多；(2)ω2=722.6 rad/s时，包装件中关键部件失效概率达到最大，ω2在低于或高于该频率点时，失效概率均下降，因此在进行产品设计时，尽量使ω2远离该频率范围；(3)ξ1eq和ξ2的增加可有效降低关键部件的损坏概率，且可有效减小失效概率峰值频率范围，对比图7(b)和图7(c)，增加ξ1eq对于减小失效概率的效果较增加ξ2要好的多；这表明，关键部件失效概率对参数ξ1eq的敏感性较大。在进行包装设计时，可充分利用这一特性，提高缓冲材料等效阻尼比，以降低包装件损坏概率；(4) 随着质量比μ的增加，易损件的损坏概率降低，且损坏概率峰值所在的频率点有所右移；(5) 脆值Gc的增加可有效降低损坏概率。

5 结 论

本文考虑了包装件中的关键部件，研究二自由度非线性包装系统在真实的具有多峰值PSD特征的随机振动条件下的可靠度，并分析参数变化对可靠度的影响。考虑到真实随机振动的谱特征，应用多阶Kanai-Tajimi模型模拟该多峰谱特征，建立了应用谱矩法识别模型参数的具体步骤，将该随机振动离散化表示在标准正态随机变量空间中。对于非线性包装件，应用模型修正因子法将其等效表示为线性系统，采用一阶可靠性方法分析包装件的稳态失效概率。应用以上方法分析包装系统参数变化对损坏概率的影响，分析结果表明，为降低包装件中关键部件损坏概率，在进行包装设计时，固有频率ω1eq和ω2应合理设计，避开高损坏概率峰值区。增加等效阻尼ξ1eq和阻尼ξ2均可有效降低损坏概率，ξ1eq对损坏概率的影响比ξ2大得多。质量比μ和脆值Gc的增加也可有效降低损坏概率。

本文构建了二自由度非线性包装件在真实的具有一定谱特征的随机振动激励条件下的损坏概率评估方法，该方法为包装件振动可靠度的分析提供了一种有效的手段，本文分析的包装件中各结构参数的变化对损坏概率的影响分析对于包装设计、包装件优化提供了依据，具有良好的现实指导意义。