基于Adaboost-SVM组合算法的爆破振动强度预测研究
2019-10-10汪旭光杨仁树
梅 比, 汪旭光, 杨仁树
(1.中国矿业大学(北京) 力学与建筑工程学院,北京 100083; 2.北京矿冶研究总院,北京 100160)
随着爆破技术的日趋成熟和广泛应用,爆破振动危害问题也日益突出。尤其是在核电站、地铁等重要项目建设过程中控制爆破振动危害尤为重要,因此准确预报爆破振动强度的需求愈发迫切[1]。由于影响爆破地震波的随机因素多、非线性强,这些因素若都作为预测模型的输入参数,会增加模型冗余度,对预测速度和准确性造成不利影响。
主分量分析[2](Principal Component Analysis,PCA)法是一种统计分析方法,可以高效地找出数据中的主要部分,将原有的复杂数据降维,去除整个数据中的噪音和冗余。支持向量机(Support Vector Machine,SVM)能够根据有限的样本信息在模型的复杂性和学习能力之间寻求最佳折衷,以获得最好的推广能力[3]。该方法主要用于模式识别,近年来已推广到线性和非线性系统的回归估计中。自适应提升算法[4](Adaboost)是一种高效的迭代算法,能够对各种方法构建的弱分类器进行有效筛选和组合,从而构成强分类器,其最大优点就是自适应性强,不会出现过拟合情况[5]。在爆破振动预测方面,国内的陆凡东等[6-8]利用SVM对爆破振动强度作了预测研究,但他们对输入因素参量的选择大多依靠经验选取,缺乏量化分析指导。
本文依靠某重点爆破工程的振动监测实测数据,在用PCA法科学选取主影响因素的基础上,结合径向基SVM分析法,建立了预测模型。为了进一步提高对爆破振动强度的预测精度,首次将Adaboost与SVM方法结合,提出了Adaboost-SVM组合算法,并成功运用于爆破振动强度的预测,使预测精度得到了进一步提高。
1 爆破振动测试及监测数据
在某核电站爆破工程中,对核岛区重点保护部位进行了爆破振动监测,并从监测数据中选取了35组有效样本数据作为研究对象。部分数据列于表1。本文选取质点振动加速度峰值作为衡量爆破振动强度的物理量,预测对象即为监测点爆破振动信号的质点振动加速度峰值。
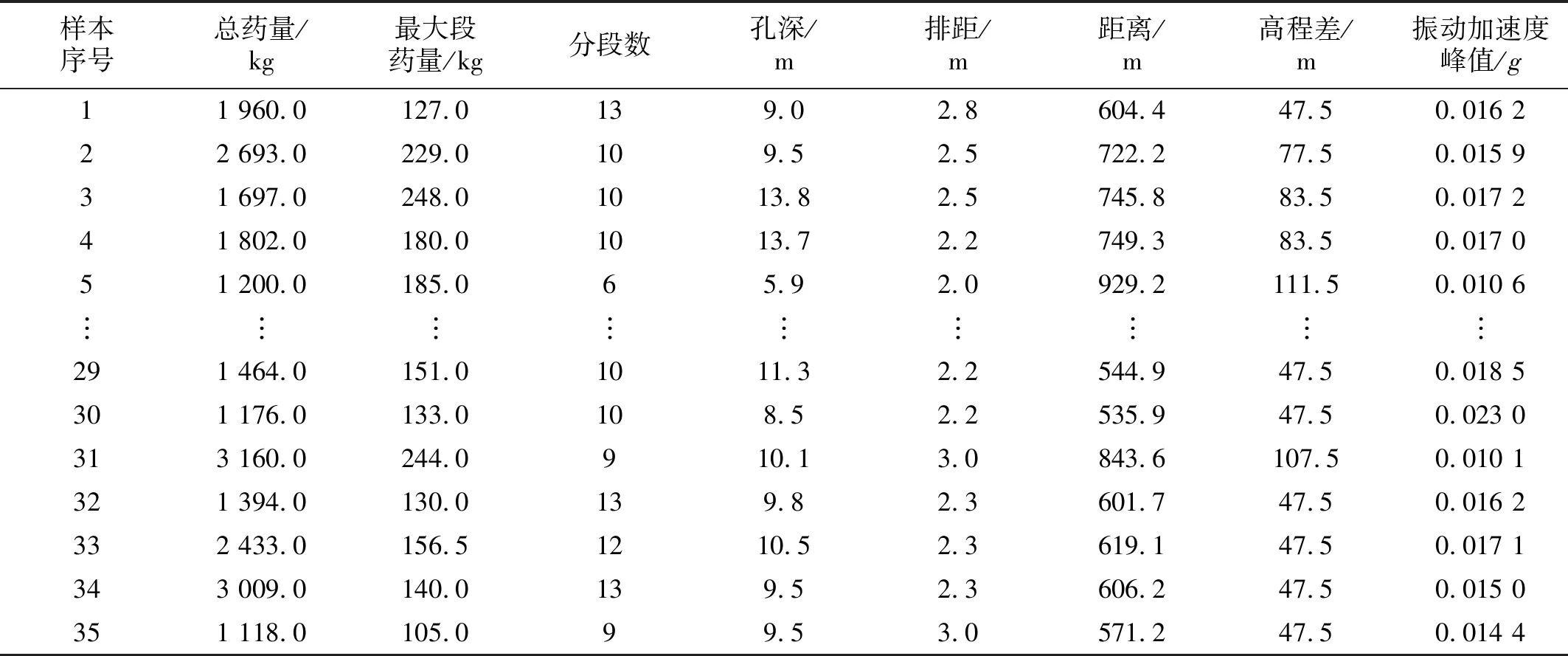
表1 爆破振动试验监测结果Tab.1 Monitoring results of blasting vibration test
2 方法原理
2.1 主分量分析法
由于原始数据的变量基数比较复杂,难以描述其特征,主分量分析提出了一种简单解决问题的思想,从事物的主要方面进行重点分析[9]。该方法认为某个事物的特征集中在几个主要变量上,只需要将这几个变量分离出来,对这几个变量进行重点分析,用它们的线性组合表示事物的主要特征[10]。
PCA方法可描述为:寻找一组正交基组成的矩阵P,定义Y=PX,使得CY=MYYT是对角矩阵。P的行向量,就是数据X的主分量,也就是XXT的特征向量,矩阵CY对角线上第i个元素是数据X在方向Pi的方差[11]。
主分量是n个原始变量的线性组合,各主分量之间互不相关[12]。每个主分量对应一个方差,该方差为协方差阵对应的特征值,各主分量特征值之和为1。将主分量按照其对应的方差值从大到小依次排列,则最大的方差对应第一主分量,以此类推。选择主分量的数量取决于保留部分的累积方差在总方差中所占的百分比。由于所有主分量的总方差值是确定的,前面变量的方差较大,则后面的变量方差就较小。只有前几个综合变量才称得上是主分量,后几个综合变量为次分量。一般情况下,可根据问题的实际需要,主观地确定一个百分比值,当前x项的方差之和大于此百分比值时,就可以决定保留前x个主分量,而忽略后面的次分量。
2.2 支持向量机回归
给定样本{(xi,yi)|i=1,2,…,n},xi∈Rd,yi∈R。这里xi表示输入向量,yi为输出向量。对于这个非线性函数回归问题,采用一个非线性映射φ(·)将样本从原空间映射到维数为k的高维特征空间中,然后在高维特征空间中进行线性回归,从而取得在原空间非线性回归的效果[13]。设线性回归函数为
F={f|f(x)=wT·x+b,w∈Rk}
(1)
式中:w为权向量;b为常数;b∈R。按照最优化理论中凸二次规划的解法,通过函数变换,非线性函数回归问题可以转化为求解非线性规划问题,则函数f(x)可以表示为
(2)
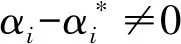
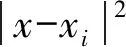
(3)
式中:σ2为宽度系数。
2.3 Adaboost-SVM组合预测模型
Adaboost作为一种迭代提升算法,其基本思路是把多个不同的弱分类器集成,从而构成一个强分类器[15-16]。本文采用的Adaboost-SVM算法是把基于PCA特征子空间的多个SVM预测模型作为弱分类器,尔后通过Adaboost算法构成强分类器。其具体步骤如下:
步骤1给定一个训练样本{(x1,y1),…,(xn,yn)},样本数据的初始分布权值为D1(i)=1/n,i=1,2,…,n。设进行T次循环迭代,初始化迭代次数为t=1。
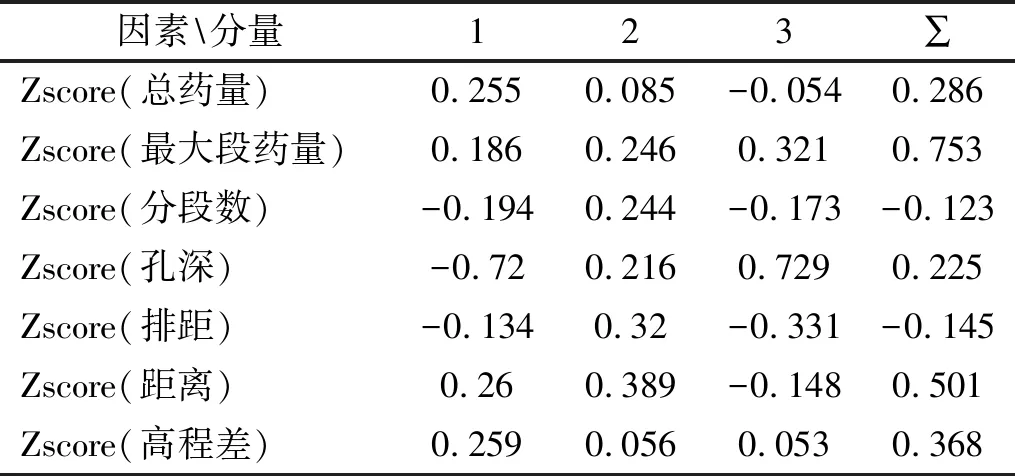
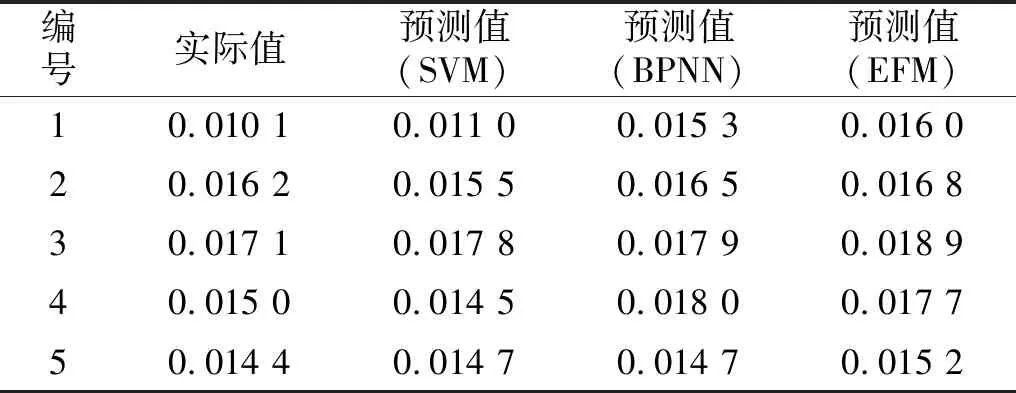
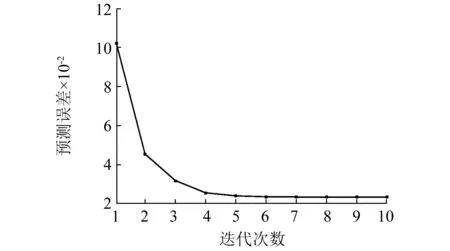
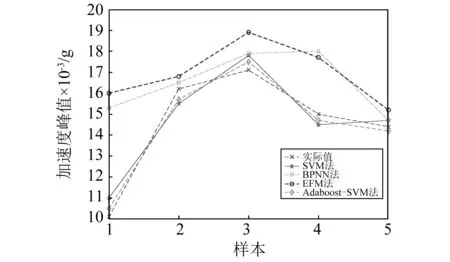
步骤2按初始权重分布从训练样本中选取m组训练样本子集(m 步骤5更新样本权重 步骤6令迭代次数t=t+1。 步骤7若t 步骤8组合强分类器 将振动加速度峰值设为被解释变量Y,将总药量、最大段药量等7个影响因素指标设为解释变量x1,…,x7。从表1中选取了前10个样本数据,构成了观测数据矩阵X。按照以下步骤作PCA法分析: 步骤1对原始数据进行标准化处理,消除量纲的影响。 步骤2计算原始变量样本观测数据经标准化处理后所得数据的协方差矩阵S。 步骤3计算S的所有特征根及其对应的特征向量,并按特征根λj的大小顺序将它们进行排序。 步骤4计算各主分量的贡献率、累计贡献率及各变量的信息提取率。 步骤5根据步骤4的参数来判定选择主分量的个数及种类。在实际中,一般要求主分量的累计贡献率要达到85%以上。同时,还要考虑到某个原始变量在所选取的主分量中所能反映的程度。 经过计算,得到前2个主分量的累积贡献率为75.6%,前3个为88.4%,前4个为94.7%。可见,选取前3个主分量就可以足够表示主要信息。本文利用分量得分系数矩阵中各因素得分系数之和排序,得出了用于SVM预测模型的主分量因素,分量得分系数矩阵见表2。 表2 分量得分系数矩阵Tab.2 Matrix of component score coefficient 从表2数据可知,7种因素在主分量里的得分权重依次为最大段药量、距离、高程差、总药量、孔深、分段数和排距,前3种因素的数值高出较多。结合实际分析,总药量的影响小于最大段药量,是由于微差爆破所决定的;一旦总药量和各段药量确定,分段数也就随之确定;各样本的排距一般变化不是很大,而且考虑到破碎效果,排距在设计时受限于孔深和段药量等参数。所以,本文用于SVM预测模型的特征参数确定为最大段药量、爆源到测点距离和高程差这3组参数。 将表1中样本序号1~30作为训练样本,样本序号31~35作为预测样本。经过对表1中数据的标准化处理,得到去量纲后的数据,建立训练样本集 {(xi,yi),i=1,2,…,30},xi∈R3,yi∈R 式中:xi为3维输入向量;yi为1维输出向量;X为训练样本输入向量,其为n×l的矩阵;Y为训练样本输出向量,其为1×l的矩阵;Z为预测样本输入向量,其为n×l’的矩阵。这里,n=3,l=30,l’=5。 采用径向基核函数和序贯最小优化算法来训练模型,在MATLAB上编程实现。模型中需要确定的参数有核函数的宽度系数σ2、惩罚因子C以及不敏感系数ε。ε控制模型拟合误差的大小,σ2和C控制着模型的复杂程度,反映模型训练拟合和预测精度的折衷。根据模型特点,ε从0.000 01~0.1按5个数量级分别取值。图1反映了训练样本在不同ε值下的回归拟合结果。 图1 不同ε取值时训练样本的拟合结果Fig.1 Fitting results of training samples in different ε values 从图1可知,当ε=0.01时拟合值与实际值相差较大,说明产生欠拟合;ε=0.001时拟合曲线已经比较接近实际值曲线;而当ε=0.000 1和ε=0.000 01时,除个别样本点外,拟合值与实际值相差无几,但为了避免因为过拟合而影响模型的泛化能力,这里取ε=0.001比较合适。(ε=0.1时拟合值均为负值,未标出)。σ2和C的取值采用交叉验证法。经过计算,得出最优参数为σ2=8,C=26。 根据以上参数确定预测模型后,输入预测样本对振动加速度峰值进行预测。将预测结果与BP神经网络法[17](Neural Network,NN)、经验公式法[18](Empirical Formula Method,EFM)的预测结果对比,结果见表3。3种方法的预测值的平均相对误差分别为:4.55%,16.02%和19.24%。 表3 各模型预测结果对比表Tab.3 Forecasting results of each model 由此可见,SVM模型的爆破振动强度预测精度达到了95.45%,要高于其它两种模型。此外,把经PCA法确定的3因素和未作处理前的7因素这两种样本条件,即输入矩阵规模分别为3×30和7×30,用SVM算法进行训练,在同一配置的计算机硬件和软件环境中,其收敛时间分别为5 s和28 s,说明经过PCA算法确定主因素后,预测模型的算法速度提高了5倍以上。 为了进一步提高爆破振动预测精度,以PCA算法得出的3种特征参数作为输入参量,将训练样本子集均分为3组(即将序号1~30数据分为3组)分别建立SVM模型,作为弱分类器,通过Adaboost提升算法构建一个强分类器,而后采用测试集数据对强分类器进行校验。其中,设置迭代的终止条件为et=0或迭代次数T=10。最终得到该算法迭代次数与预测误差之间的关系,如图2所示。 图2 预测误差与迭代次数的关系Fig.2 Relationship between prediction error and iteration number 由图2可知,随着迭代次数的增加,该模型的预测误差也逐渐降低,但当第6轮迭代预测误差降低到2.56%后趋于稳定,表明终止迭代的条件是预期设定的迭代次数,而非et=0。经过该模型迭代计算,预测精度提升到了97.44%,且6次迭代即可。其对应的序号31~35样本的预测值依次为:0.010 5,0.015 7,0.017 5,0.014 7,0.014 2。为了与前文中几种方法预测效果作直观对比,图3绘出了各方法的预测值与实际值的曲线图。 图3 各种方法预测值与实际值的曲线图Fig.3 Diagram of forecasting values & practical values in each way (1) 所提出的基于Adaboost-PCA-SVM综合算法模型,可用于预测爆破振动加速度峰值。通过PCA分析法有效约简了影响爆破振动强度的次要因素和冗余数据,确定了3个主因素。经过SVM模型的训练优化,实现了对爆破振动加速度峰值的预测,最后通过Adaboost算法与SVM相结合,构建强分类器模型,进一步提升了预测精度。 (2) 计算结果表明,经过PCA因素优化后的SVM模型的预测精度达到了95.45%,远大于经验公式法和BP神经网络法得到的结果,且算法速度得到提高;提出的Adaboost-SVM组合算法能够进一步将预测精度提高至97.57%,该模型方法具有较高的推广应用价值。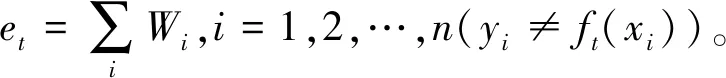

3 爆破振动强度预测及结果分析
3.1 PCA法确定模型输入参数
3.2 SVM模型的训练和预测

3.3 Adaboost-SVM组合算法
4 结 论
