TBM隧道管片的环向变形性能
2019-09-24陈孝国刘纪峰张会芝
陈孝国,杨 悦,刘纪峰,张会芝,陈 稳
(1.三明学院 信息工程学院,福建 三明 365004;2.黑龙江科技大学 理学院 黑龙江 哈尔滨 150022;3.三明学院 建筑工程学院,福建 三明 365004;4.工程材料与结构加固福建省高等学校重点实验室(三明学院),福建 三明 365004;)
我国煤炭的开采深度逐年加深,深部煤巷的建设日益显得重要,其设计和施工技术逐渐成为研究热点。过去,深部煤巷的开拓方式主要采用竖井方式。 后来随着皮带运输设备的技术提高,斜井运输应用越来越多。 国内外已有数例采用TBM 施工修建的深部煤矿长大斜井项目顺利完成[1],填补了我国TBM 在长距离大坡度煤矿斜井建设领域的技术空白,开创了煤矿斜井施工新模式。但该方法在深部煤矿斜井建设中的应用尚不成熟,相关的理论研究还较浅。
张厚美[2-3]以管片接头仿真模型试验为基础,给出了不同偏心距的接头抗弯刚度系数的变化范围。F.I.Shalabi[4]对几种管片接头进行了实物试验,得出了不同荷载组合下的接头抗弯刚度的变化情况,并且对接头在多次重复荷载下的力学及防水性能进行了深入的分析。 苏许斌[5]在广州地铁管片结构试验、衬砌环缝遇水膨胀橡胶密封垫耐压性能试验的基础上,建立了考虑接头密封垫影响的接头力学模型。 2003年建设的外径13.75 m 的德国易北河第四隧道,何川[6]为了验证衬砌管片结构的承载能力和稳定性进行了1∶1 整环管片试验。试验过程中活塞千斤顶通过拉杆对衬砌管片圆环施加压力,该方法简单、传力可靠,为进一步开展相关试验提供了参考。 李京爽,王哲[7]等对管片衬砌环向接头刚度进行了试验,得到了管片衬砌环向接头处的弯矩-相对转角关系曲线。 王彪[8]对上海崇明越江隧道衬砌进行了整环试验,进行了整环试验的加载和相应加载设备的设计,并同以往衬砌加载试验结果进行了对比,为相关试验提供了重要的参考。 因此,考虑橡胶垫作用的管片结构变形性能的研究有其必要性,将为今后隧道工程的管片设计提供一定的参考和技术支持,也关系到地下工程的稳定及安全,具有极为重要的理论意义与实践意义。
1 管片结构环向受力与变形理论公式的推导
1.1 基本假定
TBM 施工隧道的支护体系一般采用钢筋混凝土管片支护, 管片和管片之间的接缝采用橡胶垫密封,起到防水作用。 由于橡胶垫的高压缩性,给整个管片环的变形性能会带来一定影响。 因此,管片的环向变形应当包括两部分,即一部分是混凝土材料本身的压缩变形,二是橡胶垫材料自身的变形。 二者之和为整环的压缩变形量,而此压缩变形量又进一步造成环形的直径发生一定的变化。 为了便于解析计算,需进行如下5 点假设。
(1)环向变形是均匀的,不考虑拱顶和拱底的区别;
(2)环向的变形量和半径的变化量之间符合集合关系;
(3)管片变形属于小变形范畴,橡胶垫属于大变形材料;
(4)围岩和管片的接触、管片和橡胶垫之间的接触均属于均与接触,不考虑非均匀接触;
(5)围岩属于理想的弹塑性材料,且各项同性。
1.2 管片结构环向受力与变形解析思路
管片环受力的力学模型如图1 所示, 外部受围压p1作用。
对于此力学模型, 外径与内径之比为以及管片厚度与外径之比均较小,所以按薄壳理论考虑。
先求围岩压力p1与管片环周长变化量Δl 的关系式,周长变化量Δl 有混凝土管片周长变化量Δl1和橡胶垫周长变化量Δl2两部分,再转化为围岩压力p1与管片环半径变化量Δr 间的关系式。继而求围岩压力p1与管片环半径变化量Δr 间的关系式,半径变化量Δr 有混凝土管片半径变化量Δr1和橡胶垫半径变化量Δr2两部分。
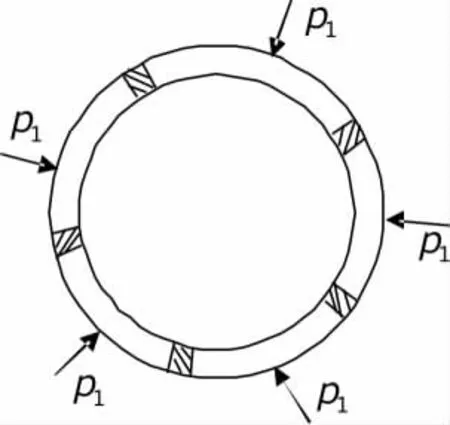
图1 管片环向力学模型(阴影处为橡胶垫)
1.3 管片环混凝土部分环向长度变化量的求解
首先要判断作用在薄壁混凝土圆柱壳上的围岩压力p1是否在它的临界压力pcr的可控制范围内。
对于薄壁混凝土圆柱壳,作用在它周围的临界径向压应力pcr由公式(1)[9]求解,

式中E1为混凝土的弹性模量;μ 为混凝土的泊松比;h 为混凝土圆环的厚度;a 为混凝土圆环的外半径。
由公式(1)可以得出:混凝土圆环的临界压力只与它的材料和它的厚度与直径之比有关,而与其它无关。
即要满足作用在圆柱混凝土薄壁壳上的围岩压力不大于它的临界压力,即式(2)

由围岩压力引起的环向压应力为

又由材料力学基本公式

可知混凝土圆环的环向长度变化量为

综合公式(3)~(5)可得

1.4 管片与管片间橡胶垫的压缩变形量引起的管片环向长度变化量Δl2的求解
先求作用在管片与管片间橡胶垫上的力即环向作用力, 将此力转化为应力, 再由橡胶垫的应力-位移拟合曲线的拟合公式确定橡胶垫的压缩位移。 室内试验确定的橡胶垫材料的应力-位移关系拟合公式为[9]

利用薄壁圆柱壳来求解管片环向作用力有以下公式[10-11],

式中 β=(3(1-μ2)/(h2a2))1/4;D=E1h3/(12(1-μ2));Δr1是混凝土管片环径向位移变化量;p1是围岩压力;E1是混凝土弹性模量;h 是管片环厚度;a 是管片环外半径;μ 是材料的泊松比;查询混凝土规范取值。
式(8)化简后为下式

又由材料力学基本公式有

式中A 是管片与管片间橡胶垫的受压面积。
联立公式(9)和公式(10)可得出作用在橡胶垫上的应力σ 为

式中 β=(3(1-μ2)/(h2a2))1/4,D=E1h3/(12(1-μ2))所有参数意义同上。
把σ 的值代入到橡胶垫的应力-位移拟合曲线的拟合公式(7)中,便可以求出橡胶垫的单片压缩量Δl2的计算式为

1.5 管片半径变化量
综合公式(6)和公式(12)可得管片半径变化量为

式中0.269 3 MPa<σ<88.15 MPa,因为管片环各管片之间有7 片橡胶垫组成,故取7 倍的单片橡胶垫压缩量 Δl2。 ,β=(3(1-μ2)/(h2a2))1/4,D=E1h3/(12(1-μ2)),所有参数意义同上。
由于斜井有一个6°的倾角,故作用力在倾角方向会有一定的分解,但这个分解作用力极小,对计算结果几乎没有影响,故以上理论公式的推导没有考虑这个倾角的影响。
2 案例计算
2.1 管片环向变形量计算
神华“新街台格庙”矿区位于鄂尔多斯高原的中南部,具典型的高原堆积型丘陵地貌特征(为沙漠~半沙漠地区),地表几乎全部被第四系风积沙所覆盖,植被稀疏。 根据总体规划、环境及煤层赋存条件,将规划的一号矿井主、副斜井分别作为本次工程试验的1#、2# 试验井。1#、2# 试验井井口标高1 320 m,落底+660 m,6 度布置,总长度均为6 314 m,其中斜井井口205 m 采用明挖法施工,明挖段包括步进段189 m、始发段16 m;TBM 施工段长度为6 109 m,半径为3.65 m。 TBM 施工段从上到下穿过的岩层分别是白垩系下统志丹群、侏罗系中统安定组、侏罗系中统直罗组、侏罗系中统延安组。
巷道衬砌管片结构内半径b=3.3 m,外半径a=3.65 m,管片的宽度d=1.5 m,厚度h=0.35 m,围岩压力 p1取 15 MPa,管片混凝土 C40,密度 ρ=2 440 kg/m3,泊松比 μ=0.22,弹性模量 E1=3.25×104MPa,橡胶垫的弹性模量用E2表示。
首先要判断作用在薄壁混凝土圆柱壳上的围岩压力p1是否在它的临界压力pcr的可控制范围内。
也就是说作用在薄壁混凝土圆柱壳上的围岩压力p1在它的临界压力pcr的可控制范围内。
将各参数值代入到公式(11)有

故作用在橡胶垫上的应力在它的破坏应力控制范围内。
把σ 的值代入到公式(12)中,便可以求出单片橡胶垫的压缩量Δl2的值综上,管片半径变化量 Δr 为
2.2 同等条件下巷道围岩环向变形位移计算
围岩环向变形公式[12]为

式中u 为围岩环向变形量,v 为围岩泊松比,E 为围岩弹性模量,a 为围岩半径,P1为外压(取15 MPa)。
将各参数值代入公式(14)中,得
通过对以上工程实例具体的计算数值与巷道围岩环向变形位移数值的对比,巷道围岩环向变形位移小于工程实例具体的计算数值,主要是由于管片间的橡胶垫弹性压缩活动位移的影响,即验证了理论公式推导的正确性和可靠性。
由于斜井有一个6°的倾角,故以上算例的作用力在倾角方向会有一定的分解,但这个分解作用力极小,对计算结果几乎没有影响,故以上算例没有考虑这个倾角的影响。
3 结论
先后推导了管片环混凝土部分环向长度变化量、管片与管片间橡胶垫的压缩变形量引起的管片环向长度变化量、管片半径变化量等计算表达式。 通过神华新街台格庙矿区试验井1# 井TBM 施工段的实际工程数据,验证了所得理论解的正确性和合理性。 进而根据管片半径变化量与围压压力的关系,求得了同等条件下考虑橡胶垫作用的管片半径变化量的计算式,并通过实例计算验证其正确性和可靠性。 验证了考虑橡胶垫作用的管片结构变形性能的研究的必要性,克服了传统的设计当中未考虑橡胶垫变形带来的影响。将推进工程设计的精准化,将为今后TBM 施工隧道工程的管片设计提供一定的理论依据,也为地下工程的修建提供参考。
