基于Abaqus的橡胶垫板静刚度特性研究

杜佳桥 王少华

西南交通大学 成都 610000

0 引言

轨道橡胶垫板是铁路扣件系统的重要组成部件之一。在早期的铁路铺设中，使用的是木制轨枕，其本身具有较大的弹性，能够与碎石道床一起为线路提供必要的弹性。随着铁路技术的发展，木制轨枕被混凝土轨枕替代，而混凝土轨枕几乎没有弹性，不能很好地为线路提供弹性，故须增加轨道橡胶垫板。在有砟轨道中，线路的弹性主要由道床和橡胶垫板提供，橡胶垫板的性能就显得尤为重要。在高速铁路中无砟轨道中，道床由碎石变成了混凝土，道床几乎不能为线路提供弹性，此时线路的弹性几乎完全由橡胶垫板提供。橡胶垫板对于列车、轨道、道床等的动力学性能具有重要的影响。因此，无论是现代的有砟轨道还是无砟轨道，橡胶垫板刚度都是影响轨道刚度的重要因素之一。

1 橡胶材料本构模型

本文使用Moony-Rivlin 模型[1]模拟橡胶垫板材料。Moony-Rivlin 模型是超弹性材料中最为常用的本构模型之一，采用应变能密度函数方法，由应变偏量能和体积应变能两部分组成，其应变能密度函数为

式中：U为应变能密度，N为多项式阶数，I1、I2为应变张量的两个主不变量，Di是材料不可压缩常数（当Di=0 时完全不可压缩），Cij为材料决定的常数，J为材料变形前后体积比。

根据N取值的不同，常用的Moony-Rivlin 模型有2 参数、3 参数、5 参数、9 参数模型。Abaqus 有限元分析软件能够很好地模拟橡胶材料[2]，其提供了2 参数模型，表达式为

Moony-Rivlin 模型适用于形变30%以内（受压）、形变100%以内（受拉）的中小变形[3]，橡胶垫板属于受压情况，且正常情况下形变量小于30%，适合用Moony-Rivlin 模型进行橡胶垫板的模拟。

2 橡胶垫板仿真参数的计算

使用Abaqus 中Moony-Rivlin 模型进行橡胶垫板的模拟，在材料参数设置时，需设置参数C10、C01、D1。通常情况下，要获得这3 个参数需要进行试验进行测定[4]，由于试验条件限制，采用近似计算的方法进行参数的计算。橡胶垫板的剪切模量G与橡胶垫板的邵氏硬度（HS）如式（6）所示，可根据该关系，由橡胶垫板的邵氏硬度计算出它的剪切模量

剪切模量G与C10、C01的关系为

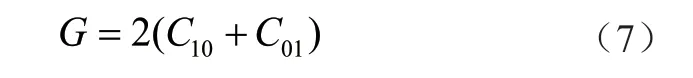
C01/C10与橡胶垫板的邵氏硬度的经验关系如图1 所示[5]，可以据此橡胶垫板的邵氏硬度得到C01/C10的比值，再与式（7）联立即可求出C10、C01的值。

图1 C01/C10 与邵氏硬度关系

材料不可压缩常数D1与体积模量K有关系为

材料的体积模量K与弹性模量E、泊松比μ关系为

材料的弹性模量E与剪切模量G、泊松比μ关系为

联立式（8）～式（10）可得

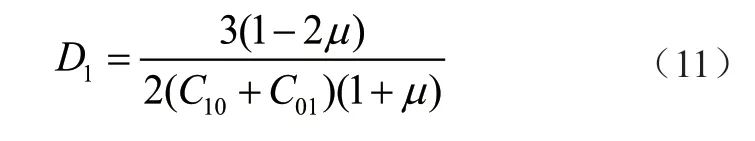
根据式（11）即可由泊松比计算出D1，特别的，当橡胶垫板视为完全不可压缩时，即泊松比为0.5，此时D1取值为0，至此可以算出2 参数Moony-Rivlin 模型中需要的三个参数。

根据弹条Ⅴ形扣件组装暂行技术标准，橡胶垫板邵氏硬度应大于等于65°，本次仿真中取邵氏硬度为80°，C10为0.887 MPa，C01为0.009 MPa，D1为0.002 24 MPa-1。

3 橡胶垫板静刚度特性

橡胶垫板的静刚度计算公式为

式中：KSTA为橡胶垫板的静刚度，F1、F2分别为向橡胶垫板施加的最小和最大荷载，分别取20 kN 和80 kN。D1、D2分别为荷载为F1和F2下的橡胶垫板位移。

以P60-10-11 型橡胶垫板作为计算对象，P60-10-11 中P60 代表适用于60 kg/m 钢轨，10 代表垫板厚度为10 mm，11 代表沟槽数为11 个。橡胶垫板的前后左右是对称的，且上下表面受力均匀，因此，为了减小计算量，提高计算精度，采用1/4 模型进行计算，图2 所示为建立的橡胶垫板模型。图3 所示为橡胶垫板的y向位移云图，图4 所示为橡胶垫板的荷载与位移的关系。

图2 橡胶垫板模型

设计沟槽的目的之一也是为了减小橡胶垫板的静刚度，由图3 可知，橡胶垫板在受压时，沟槽处变形较大。

图3 橡胶垫板y 向位移云图

由图4 并根据式（12）可以计算出橡胶垫板的静刚度为98.4 kN/mm，但是可以明显看出，橡胶垫板的荷载与位移曲线并不是线性关系，荷载随位移的增大迅速增加，即静刚度在迅速变大，在位移达到1 mm 左右时，此时橡胶垫板的静刚度为162.6 kN/mm，相对式（12）可以计算的静刚度增大了65.2%。因此，在许多的研究中将扣件系统的刚度看作定值或许对研究结果有一定的影响。

图4 橡胶垫板荷载位移曲线

3.1 摩擦系数对橡胶垫板静刚度的影响

轨道与橡胶垫板之间、橡胶垫板与轨枕之间都是摩擦接触。橡胶与钢之间的摩擦系数为0.8 左右，橡胶与橡胶之间摩擦系数为0.5 左右，橡胶与混凝土之间为0.3左右。有许多因素都会引起摩擦系数的不同或变化，比如混凝土轨枕的表面粗糙度不同，钢轨表面发生锈蚀，接触面之间混入细砂等都会使摩擦系数不同或者发生变化。改变轨道与橡胶垫板之间、橡胶垫板与轨枕之间的摩擦系数，研究摩擦系数为0.35、0.5、0.65、0.8的情况下橡胶垫板的静刚度的变化规律。建立2 因子4 水平的正交试验表，并计算橡胶垫板静刚度（见表1），变化曲线如图5 所示。

表1 不同摩擦系数下橡胶垫板静刚度

由图5 可知，当垫板与轨枕间摩擦系数保持不变时，垫板静刚度随轨道与垫板间摩擦系数增大而增大。当轨道与垫板间摩擦系数保持不变时，垫板静刚度随垫板与轨枕间摩擦系数先增大然后几乎保持不变。随着垫板与轨枕间摩擦系数或轨道与垫板间摩擦系数的增大，垫板静刚度增大的趋势逐渐放缓。轨道与垫板间摩擦系数的变化对垫板静刚度的影响比垫板与轨枕间摩擦系数的变化更大。改变摩擦系数计算得到的橡胶垫板最小静刚度为91.83 kN/mm，最大静刚度为100.19 kN/mm，变化幅度为9.1%。

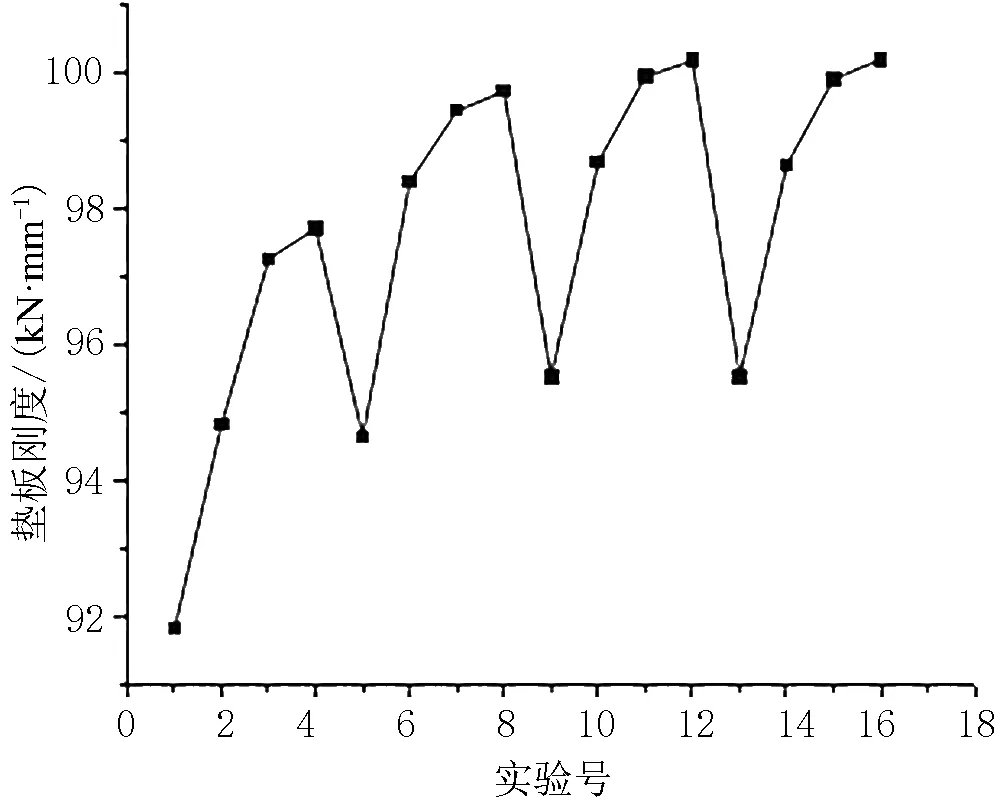
图5 橡胶垫板静刚度变化曲线

3.2 厚度对橡胶垫板静刚度的影响

橡胶垫板的厚度是橡胶型号的主要参数之一，通过改变橡胶垫板的厚度，研究橡胶垫板厚度与其静刚度之间的关系。其他参数不变，沟槽数为11，计算厚度为8 mm、10 mm、12 mm 情况下橡胶垫板的静刚度。计算出这3 种厚度的橡胶垫板的静刚度分别为111.25 kN/mm、98.4 kN/mm、83.69 kN/mm，垫板静刚度与厚度之间的关系如图6 所示，可以看出，垫板的静刚度随垫板厚度的增加而减小，且垫板静刚度受厚度变化的影响较大，近似呈线性关系。

图6 垫板静刚度与垫板厚度关系

3.3 沟槽数量对橡胶垫板静刚度的影响

橡胶垫板的沟槽数量也是橡胶型号的主要参数之一，通过初步的分析，橡胶垫板有无沟槽、沟槽的数量均对橡胶垫板的静刚度有明显的影响。其他参数不变，橡胶垫板厚度为10 mm，计算沟槽数分别为11、13、15、17的情况下橡胶垫板的静刚度。

通过计算，沟槽数为11、13、15、17 时橡胶垫板的静刚度分别为98.4 kN/mm、86.06 kN/mm、76.11 kN/mm、67.92 kN/mm，图7 所示为橡胶垫板静刚度与沟槽数量的关系。

图7 垫板静刚度与沟槽数量关系

由图7 可知，随着橡胶垫板沟槽数量的增加，垫板静刚度大幅下降，沟槽数量从11 个增加到17 个的过程中，垫板静刚度从98.4 kN/mm 减小到67.92 kN/mm，变化率为30.98%。

4 结论

本文通过公式推导，可根据橡胶的邵氏硬度近似计算出Moony-Rivlin 模型中的参数，此方法可在缺乏试验数据的情况下使用。橡胶垫板的静刚度是非线性的，在许多的研究中将扣件系统用线性弹簧模拟或许对结果有影响。

在Abaqus 中，利用Moony-Rivlin 模型对橡胶垫板进行模拟，根据计算结果可知，橡胶垫板的静刚度随摩擦系数的增大而增大，随橡胶垫板厚度的增大而减小，随橡胶垫板沟槽数的增多而减小。要根据线路实际情况选择合适的橡胶垫板，使橡胶垫板实际表现出来的静刚度满足需求。