提高监控反思 强化逻辑推理
2019-09-19郑良
郑 良
(安徽省灵璧第一中学 234200)
笔者在进行高三二轮“数列”专题复习备课时,遇到了如下两道试题,很容易就发现了其中的解答错误.而类似的运算错误在学生答题中比较常见,故撰写此文,以示提醒,以期抛砖引玉,引发更多、更好的解决方案.
一、试题与解答
例1设等差数列{an}满足:3a7=5a13,cos2a4-cos2a4sin2a7+sin2a4cos2a7-sin2a4=-cos(a5+a6),公差d∈(-2,0),则数列{an}的前n项和Sn的最大值为( ).
A.100π B.54π C.77π D.300π
解设等差数列{an}的公差为d,由3a7=5a13,得a1=-21d.
cos2a4-cos2a4sin2a7+sin2a4cos2a7-sin2a4=cos2a4(1-sin2a7)-sin2a4(1-cos2a7)=cos2a4cos2a7-sin2a4sin2a7=(cosa4cosa7-sina4sina7)(cosa4cosa7+sina4sina7)=cos(a4+a7)cos(a4-a7)=-cos(a5+a6).
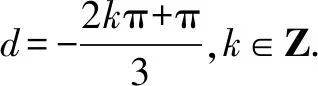
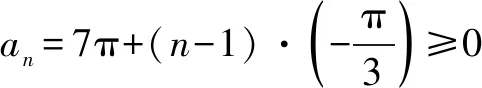
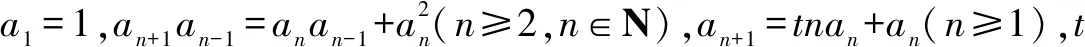



当n≥5时,n!的个位数字为0,而1!+2!+3!+4!的个位数字为3,所以所求前100项和的个位数字也是3.
二、案例剖析
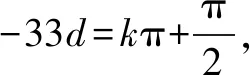
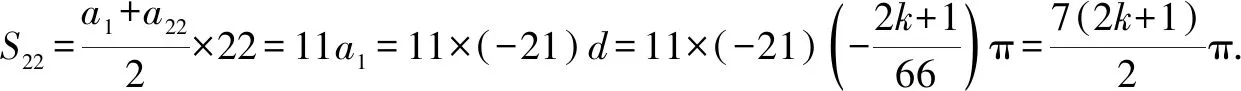
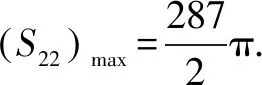

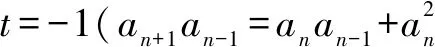
下面分别验证其充分性:
当t=1时,an+1=(n+1)an,得an≠0,以上解答成立.(或先求an=n!,再验证满足an+1an-1=an(an-1+an)),此时所求前100项和的个位数字为3.
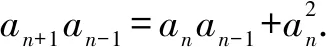
综上所述,a1+a2+…+a100的个位数是3或1.
三、两点感悟
1.深化运算能力 提高监控反思
数学运算是指在明晰运算对象的基础上,依据运算法则解决数学问题的素养.主要包括:理解数学对象,掌握运算法则,探究运算思路,选择运算方法,设计运算程序,求得运算结果.数学运算主要表现为:理解运算对象,掌握运算法则,探究运算思路,求得运算结果.运算求解能力是指会根据法则、公式进行正确运算、变形和数据处理,能根据问题的条件寻找与设计合理、简便的运算途径,能根据要求对数据进行估计和近似计算.运算求解能力是思维能力和运算技能的结合.数学运算是解决数学问题的基本手段,通过运算可以促进学生思维发展,形成规范思考问题的本质,养成一丝不苟、严谨求实的科学精神.提高数学运算素养必需夯实基础知识、通晓运算规则,具有整体意识,明确问题走向,根据不同情形适时调整的能力.
学习过程中,可通过适当的合作学习,培养检验意识和技能等方式提高自我监控能力.解决问题时尝试思考:还有哪些角度?还有哪些方法?方法与结论是否能够推广等等.自我监控能力的提高可实现根据具体问题进行自我调节从而保证了学习的效果.学生对除法运算中除数不能为零的元认识知识是具备的,但对其相关的元认知体验未必深刻,它需要较多的正例与反例的强化与感悟.例1中,在方程cos(a4+a7)cos(a4-a7)=-cos(a4+a7)两边同时除以cos(a4+a7)是至精至简的需要,也是化归与转化的体现,但解题者出现了对运算法则理解的 “暂时缺失”从而导致了错误操作.
2.强化逻辑推理 规范书写步骤
逻辑推理是指从一些事实和命题出发,依据规则推出其他命题的素养.逻辑推理是得到数学结论、构建数学体系的重要方式,是数学严谨性的基本保证,是人们在数学活动中进行交流的基本思维品质.推理论证讲究言必有据,先证后用是解题的基本规范,也是演绎推理的根基.
平时解题的书写要规范,要写清问题的原理(数学模型),尽可能做到不跳步.注重论据的落实,形成完整的推理论证链.如何求集合A和B的交集A∩B?一般有如下方法:
①平行型.先分别求出集合A,B,再求A∩B;
②递进型.在集合A(B)的基础上满足集合B(A);
③交错型.对A,B交叉使用,最终确保满足A,B.