圆锥曲线中与焦点相关的两类垂直关系

臧一赫

(天津市滨海新区塘沽第二中学 300400)

一、“切”出来的垂直

1.抛物线切出的垂直

在学习抛物线性质时，老师总结了很多奇妙的结论，这让我产生了浓厚的学习兴趣，以上1.1就是其中之一(此处不作证明).笔者利用课余时间对椭圆和双曲线进行了与抛物线相对应结论的探究和证明，并对日常学习中得到的另一种垂直关系加以归纳整理，具体如下.

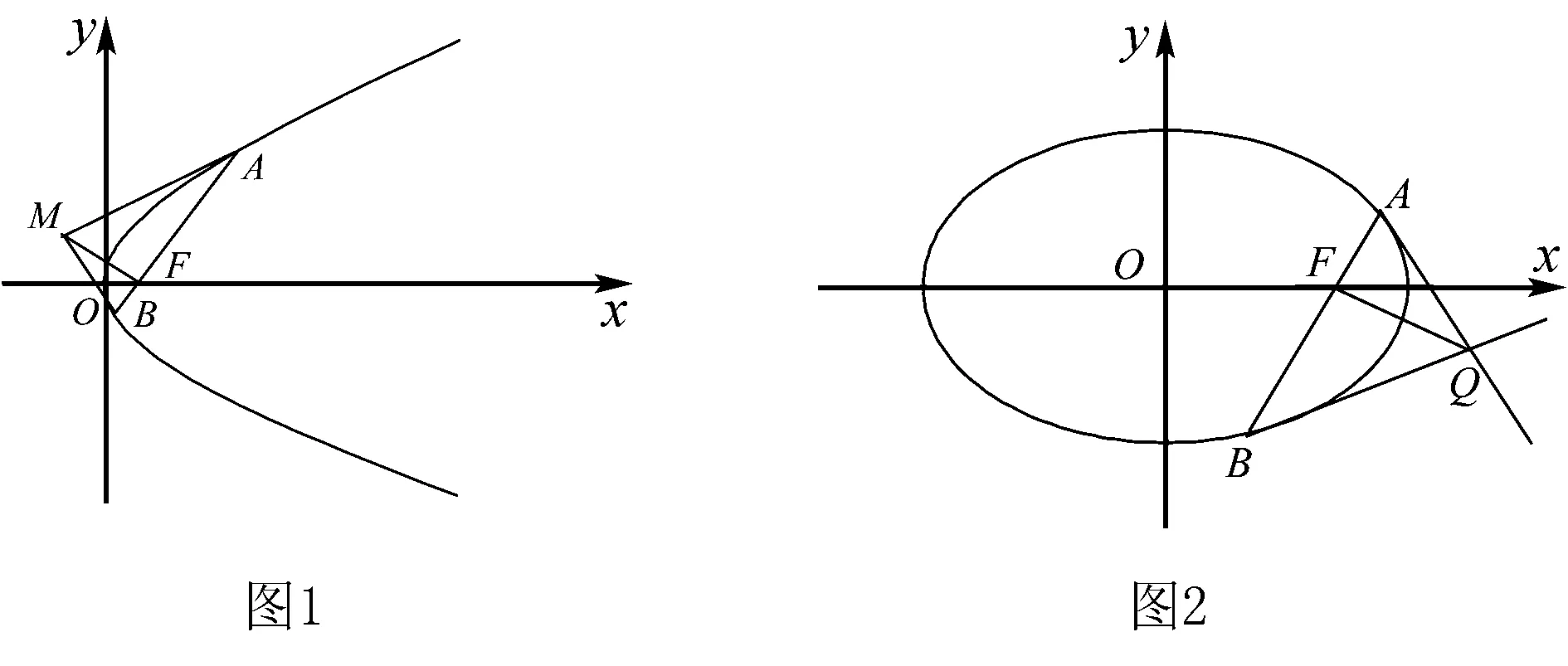
2.椭圆切出的垂直

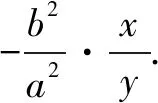
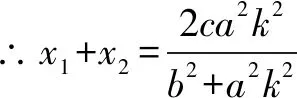
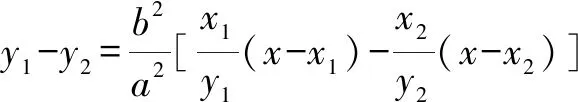
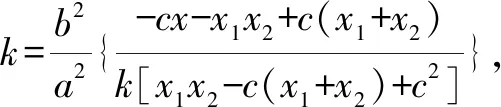
3.双曲线切出的垂直

说明其证明过程类似于椭圆相应性质的证明,此处略去不证.

二、顶点确定的垂直

1.椭圆中的垂直

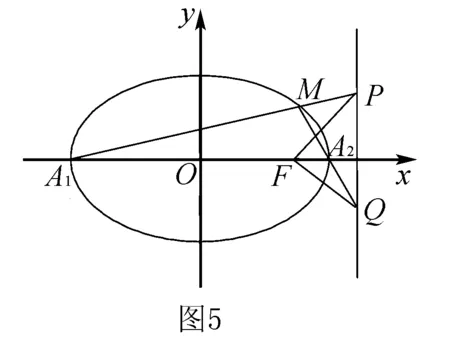
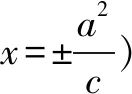
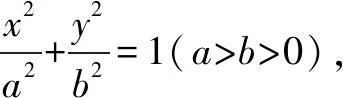
2.双曲线中的垂直

已知F为双曲线的右焦点,A1,A2分别为实轴的左右顶点,M为双曲线上异于实轴顶点的任意一点,A1M,MA2与右准线分别交于P,Q,则PF⊥QF.(证明过程类似于椭圆，此处略去)

在抛物线中可认为另一顶点在无穷远处，因此可猜想抛物线中的如下性质.

3.抛物线中的垂直

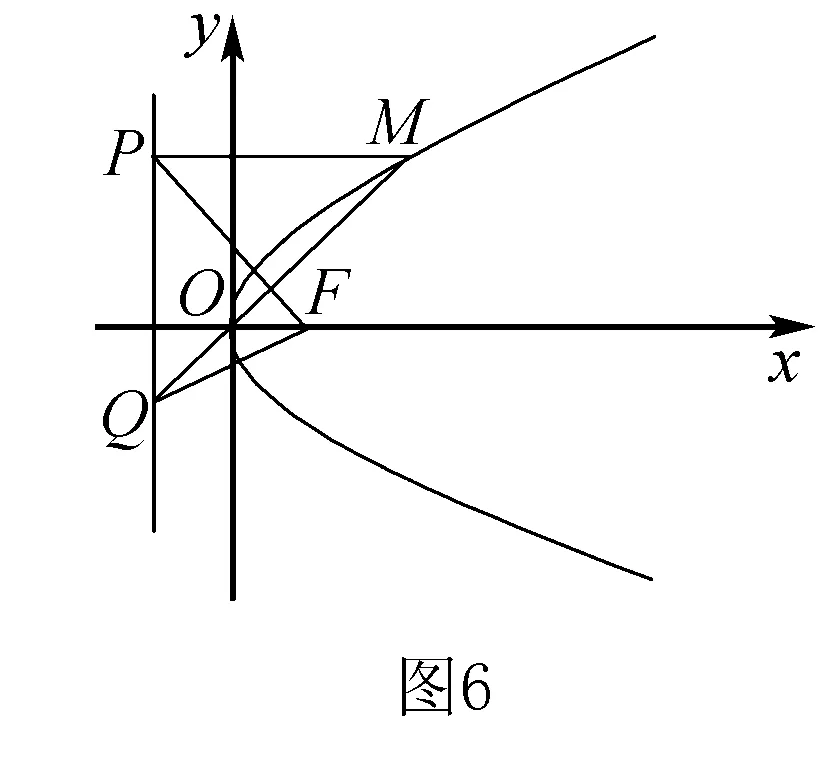
如图6，已知F为抛物线的焦点，M为抛物线上异于顶点O的任意一点，过点M作MP∥x轴交准线于点P,MO交准线于点Q，则PF⊥QF.(该性质容易证明，读者可试证)