MATLAB在常微分方程上的应用
2019-09-17赵亚琪范进军
赵亚琪 范进军
( 山东师范大学数学与统计学院, 250358, 济南 )
1 引 言
微分方程奇解的存在性、奇点的类型、极限环的存在性和零解的稳定性的判断是常微分方程理论中的重要内容[1-3], MATLAB具有强大的绘图功能且在常微分方程的抽象问题具体化方面有极大优势[4,5]. 本文从理论角度对微分方程的上述四类问题进行分析, 给出了微分方程奇点、极限环的定义及奇解的存在性、奇点类型、极限环的存在性与零解稳定性的判定方法, 鉴于理论判断较抽象, 考虑应用MATLAB的绘图功能探讨解决四类问题的新方法, 通过结合图形与理论判断达到由繁到简和形象直观解决问题的目的.
2 预备知识
2.1奇解定义设一阶微分方程
(1)
有一特解Λ:y=f(x)(x∈I).
如果对每一点P∈A, 在P点的某个邻域内方程(1)有一个不同于Λ的解在P点与Λ相切, 则称Λ为方程(1)的奇解.
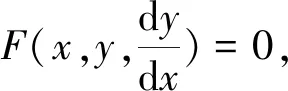
注1当常微分方程有两组积分曲线族, 且有一特解为其中一个积分曲线族的包络, 则此包络是常微分方程的奇解.
2.3一阶线性微分方程组奇点分类的直观判断依据给定二维常系数线性自治系统:

令p=-(a+d)=-tr(A),q=ad-bc=det(A).当q≠0时, 一阶线性微分方程组奇点分类的直观判断如图1所示.
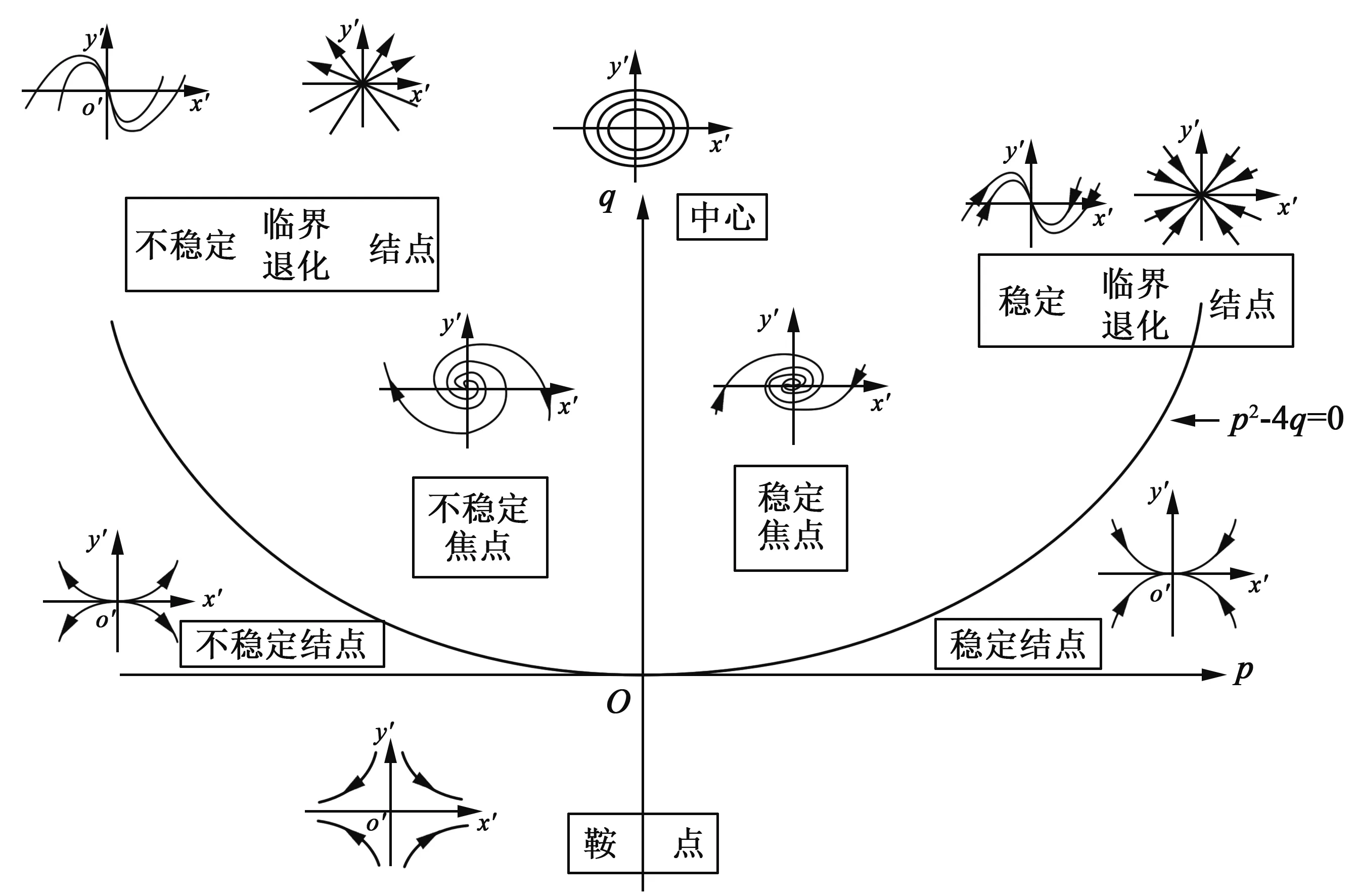
图1 奇点类型图(图形中坐标系是变换为标准方程后的坐标系x′O y′)
2.4极限环概念设系统
(2)
具有闭轨线C.假如在C充分小邻域中, 除C之外, 轨线全不是闭轨线, 且这些非闭轨线当t→+或t→-时趋近于闭轨线C, 则称闭轨线C是 (2)的一个极限环.
2.5零解稳定性的概念对于动力系统
(3)
其中:
如果对∀ε>0,t0≥0,∃δ(ε,t0)>0,∀x0∈G,只要式(3)满足初值x(t0)=x0的解x(t;t0,x0)都在t≥t0时有定义且‖x(t;t0,x0)‖<ε, 则称方程(3)的零解是稳定的.
3 MATLAB在常微分方程中的具体应用
3.1运用MATLAB判断奇解的存在性
例1考虑微分方程
(4)
易知方程通解为
(5)
y=x-C2,
(6)
显然
y=0
(7)
是方程的一个解.
运用MATLAB绘制方程(4)的第一个积分曲线族(5)(图2), 程序如下:
clear; clc; hold on;
x=linspace(-400,400,6 000);y=x-x;plot(x,y,'-k');
y1=0;
fori=-100:17:100
y1=1/27*(x-i).^3;
plot(x,y1,'-r');
end
hold off
由图2可知曲线族有包络, 故方程(4)有奇解. 同时, 观察可知方程(7)的曲线为方程(4)第一个积分曲线族(5)的包络, 故y=0是奇解.
运用MATLAB绘制方程(4) 第二个积分曲线族(6)(图3), 程序如下:
clear; clc; hold on;
x=linspace(-400,400,6 000);y2=0;
fori=-100:17:100
y2=x-i;
plot(x,y2,'-r');
end
hold off

图2 积分曲线族(5)的局部图像

图3 积分曲线族(6)的局部图像
由图3可知方程(4)第二个积分曲线族(6)无奇解.
1) 理论分析验证.由(5)与(6)得到方程(4)的通积分
它的C-判别式为
由此得到
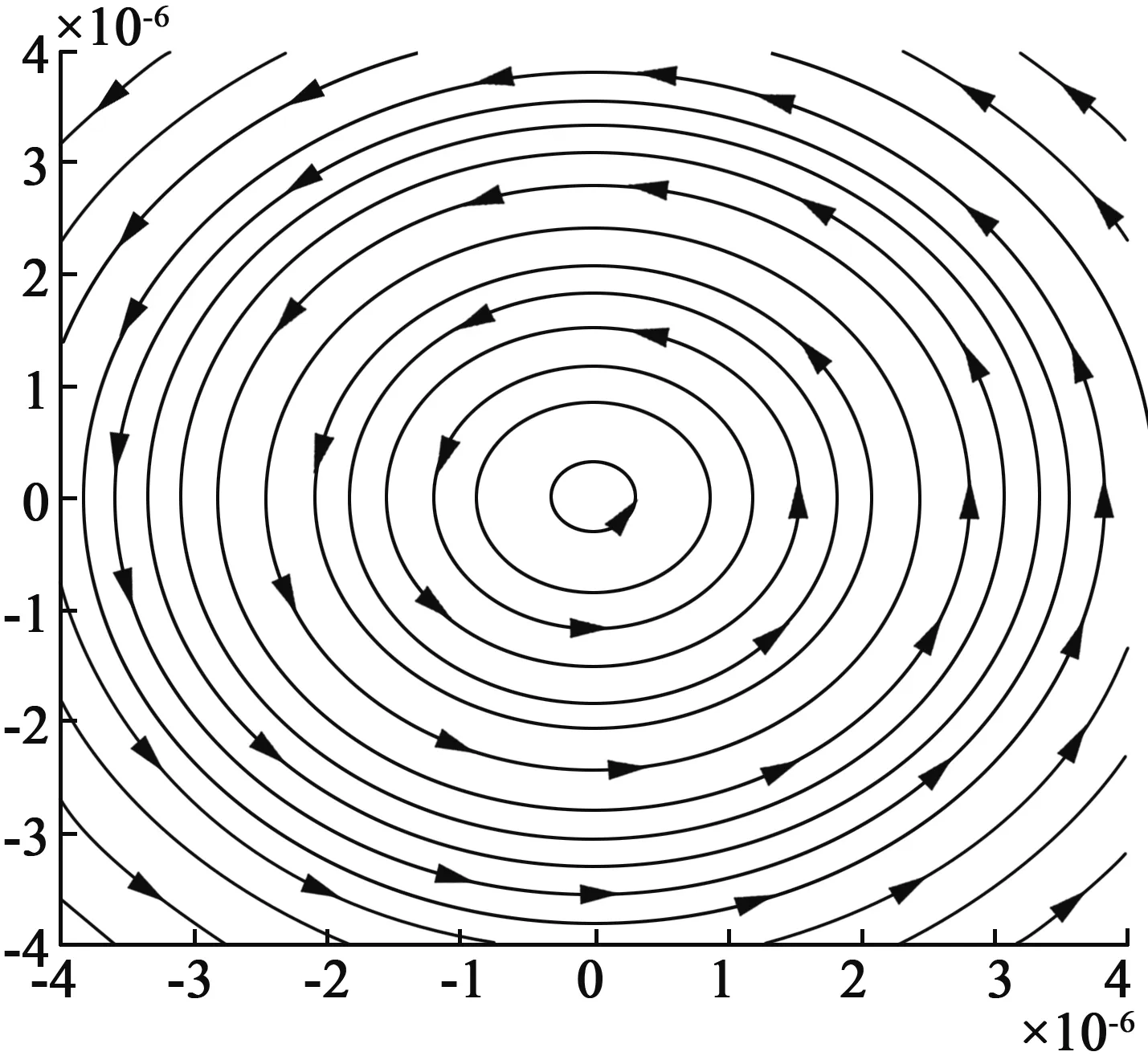
Λ:x=C,y=0(-∞ 2) 在判断奇解中MATLAB优缺点的分析. 优点:运用MATLAB绘制常微分方程的积分曲线族能够快速并直观判断出奇解的存在性. 缺点:运用MATLAB绘图是由x与y遍历区间数值得到的, 绘制出的图形有误差, 对于一些复杂的曲线族会容易出现判断失误的情况. 3.2运用MATLAB绘图判断奇点类型 例2讨论如下系统奇点类型 (8) 易知(0,0)和(-1,0)为动力系统(8)的奇点, 运用MATLAB绘制奇点附近的相图(图4), 程序如下: clear; clc;x0=-1.3:0.01:0.3;y0=-1:0.01:1; [x,y]=meshgrid(x0,y0); dx=y;dy=-x-y-x.^2-y.^2;d=sqrt(x.^2+y.^2); u=dx./d;v=dy./d; figure; streamslice(x,y,u,v); hold on; plot([-1.3,0.3],[0,0],'k','linewidth',0.5); hold on; plot([0,0],[-1,1],'k','linewidth',0.5); hold on; plot([-1,-1],[-1,1],'k','linewidth',0.5) 由图4直观观察, 易看出(-1,0)和(0,0)分别为系统(8)的鞍点和稳定焦点. 例3判断如下系统的奇点类型 (9) 运用MATLAB绘制图形(图5), 程序如下: clear; clc; hold on; x0=-0.3:0.01:0.3;y0=-0.3:0.01:0.3; [x,y]=meshgrid(x0,y0); dx=2*x+3*y;dy=2*x-3*y; d=sqrt(x.^2+y.^2); u=dx./d;v=dy./d; figure; streamslice(x,y,u,v); hold on; plot([-0.3,0.3],[0,0],'k','linewidth',0.5); hold on; plot([0,0],[-0.3,0.3],'k','linewidth',0.5) 观察图5, 易看出(0,0)为系统(9)的鞍点. 图4 动力系统(8)在两奇点附近的相图 图5 动力系统(9)在奇点(0,0)附近的相图 1) 理论分析验证.在例2中, 由 得系统(8)有两个奇点A(-1,0)和B(0,0). 对于奇点A(-1,0), 作可逆变量代换x'=x+1,y'=y, 则系统(8)可化为 (10) 系统(10)对应的线性近似系统的系数矩阵为 高次项为 φ(x',y')=0,ψ(x',y')=-(x')2-(y')2. 计算: p=-trD=-(0-1)=1>0,q=detD=-1<0,p2-4q=1+4=5>0, 从而系统(10)的奇点(0,0)为鞍点. 由于可逆线性变换不改变系统奇点的类型, 所以奇点A(-1,0)也是系统(8)的鞍点. 对于奇点B(0,0),系统(8)的线性近似系统为 (11) 相应线性近似系统(11)的系数矩阵为 高次项为 φ(x,y)=0,ψ(x,y)=-x2-y2. 计算: p=-trD=-(0-1)=1>0,q=detD=1>0,p2-4q=1-4=-3<0. 所以奇点B(0,0)是系统(8)也是系统(8)的稳定焦点. 综上所述, 运用MATLAB对例2中两奇点类型的判断正确. 类似地, 可以验证例3对奇点类型的判断正确. 2) 在判断奇点类型中MATLAB优缺点的分析.在判断奇点类型中, 运用MATLAB可以通过轨线分布的特点而快速分辨出系统中奇点的类型, 但是在通过图形直接确定奇点坐标方面容易出现偏差, 难度也较大.所以, 运用MATLAB软件绘图对于判断奇点的存在性有很大优势, 而对于奇点坐标的确定运用理论判断更方便快捷. 3.3运用MATLAB绘图判断动力系统是否存在极限环 例4判断方程组(动力系统) (12) 是否有极限环并确定极限环的位置. 运用MATLAB绘制方程组(12)的轨线分布(图6), 程序如下: clear;x0=-3:0.1:3;y0=-3:0.1:3; [x,y]=meshgrid(x0,y0); dx=y+x.*sqrt(x.^2+y.^2).*(1-(x.^2+y.^2)).^2; dy=-x+y.*sqrt(x.^2+y.^2).*(1-(x.^2+y.^2)).^2; d=sqrt(x.^2+y.^2);u=dx./d;v=dy./d; figure; streamslice(x,y,u,v); hold on;t=0:0.01:2*pi; x=@(t)cos(t);y=@(t)sin(t); fplot(x,y,'-r','linewidth',1); hold off 图6 动力系统(12)的局部相图 1) 运用理论知识验证分析.对于例4, 考察函数族V(x,y)=x2+y2=C(其中C为参数). 求V沿着方程组的全导数 G为由Γ1和Γ2所围成的环域, 则G满足Poincare-Bendixon环域定理的条件.由于r1、r2可与1任意接近, 所以单位圆x2+y2=1就是(12)的一个极限环. 可见运用MATLAB绘图对(12)极限环存在性的判断正确. 2) 在动力系统是否存在极限环的判断中MATLAB的优缺点分析.在动力系统是否存在极限环的判断中, 运用MATLAB绘图可以清晰地观察到方程组(动力系统)中x与y随时间t的增加而形成的轨线分布情况, 结合极限环的定义容易辨别极限环的存在性.但鉴于直观辨别的误差性较大, 不易得到极限环的方程式. 所以MATLAB在动力系统极限环存在性的判断中有较大优势, 可以简化问题, 但对于极限环表达式的确定需要运用理论分析得出. 3.4运用MATLAB判断动力系统零解是否具有稳定性 例5考虑如下自治系统零解的稳定性 (13) 运用MATLAB绘制图形(图7、图8): 首先, 定义函数 function [x,y,wx,wy] =H(gxy,hx,hy,nx) if nargin<4,nx=20; elsenx=nx*20; end ny=floor(nx*(hy(2)-hy(1))/(hx(2)-hx(1))); bx=(hx(2)-hx(1))/nx;by=(hy(2)-hy(1))/ny;x=hx(1):bx:hx(2); y=hy(1):by:hy(2); [x,y]=meshgrid(x,y);kk=gxy(x,y); wx=1./(1+kk.^2);wy=wx.*kk; end 绘制方程组(13)的方向场(图7), 程序如下: clc; clear; clf;gxy=@(x,y)(-y./x); hx=[-0.003,0.003];hy=[-0.003,0.003]; [x,y,wx,wy]=H(gxy,hx,hy); quiver(x,y,wx,wy,'color','b') 绘制细节图(图8), 程序如下: clear; clc;x0=-0.000 004:0.000 000 1:0.000 004;y0=-0.000 004:0.000 000 1:0.000 004; [x,y]=meshgrid(x0,y0);dx=-y;dy=x; d=sqrt(x.^2+y.^2); u=dx./d;v=dy./d; figure; streamslice(x,y,u,v) 由图8及零解稳定性定义可知, 方程组 (13)零解是一致稳定的, 但不是渐进稳定的. 图7 方程组(13)在(0,0)附近的方向场 图8 方程组(13)在(0,0)附近方向场细节图 例6判断如下系统零解的稳定性 (14) 运用MATLAB绘制(14)的轨线图(图9), 程序如下: clear; clc;x0=-0.004:0.000 1:0.004;y0=-0.004:0.000 1:0.004; [x,y]=meshgrid(x0,y0); dx=-y+x.*(x.^2+y.^2-1); dy=x+y.*(x.^2+y.^2-1); d=sqrt(x.^2+y.^2); u=dx./d;v=dy./d; figure; streamslice(x,y,u,v) 图9 动力系统(14)在(0,0)点附近的轨线图 由图9及零解稳定性定义可知, 方程组 (13)的零解是一致渐进稳定的. 2) 在动力系统零解是否具有稳定性的判断中MATLAB的优缺点分析.MATLAB在动力系统是否具有稳定性的判断中不仅可以判断出其是否具有稳定性, 还可以判断出其一致稳定性和渐进性.所以, 在动力系统是否具有稳定性的判断中, 相较于理论判断运用MATLAB绘图判断具有很大的优越性, 能够快速并准确得出结论. MATLAB在常微分方程上的运用是多方面的, 也是快速解决问题的一种方式. 运用MATLAB绘图功能在解决判断微分方程奇解的存在性、奇点的类型、极限环的存在性、零解的稳定性这四类问题上有较大作用, 不仅快捷、简便, 而且正确度高, 在不需要太过考虑误差的情况下也能够判断无误. 未来, 我们对常微分方程方面的研究可以多借助MATLAB软件, 通过绘制方程的轨线图或相图, 有助于使抽象的方程(组)或动力系统更加形象、直观, 易于理解.



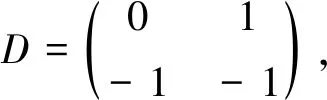






4 结 语
