浅谈二次函数在生活中应用
2019-09-10刘伟荣
刘伟荣
【摘要】 数学学科知识与实际生活联系密切,也是生活问题解决的重要工具。所以,数学知识教学要与实际生活紧密结合,既应用生活化资源辅助理解,更用生活化问题检验学生的学习情况,以实现生活与教学的深度融合。本文就初中数学教学中,二次函数在生活中的应用展开了论述,提出了二次函数与生活融合的几点建议。
【关键词】 初中数学 二次函数 生活应用 教学
【中图分类号】 G633.6 【文献标识码】 A 【文章编号】 1992-7711(2019)04-123-01
0
在二次函数这一部分内容的教学中,基于函数图像分析二次函数的性质是本节课的教学重点,而应用函数知识求解实际问题则是检测学生对函数图像、函数性质理解的重要方式。学生基于生活实际问题,应用字母和数值表示函数关系,这一过程是对学生模型意识的培养过程,也是在学生头脑中构建二次函数关系的过程。基于函数关系列出的函数解析式后,通过二次函数图像和二次函数的性质,依赖函数解析式求解出问题的答案,则是应用函数性质求解问题解答的过程。所以,在教学中将二次函数应用于生活情境和生活问题中,既能够强化学生对二次函数的理解,辅助学生应用二次函数模型解决生活问题,更增强学对二次函数问题解题的灵活性。对此,教师引导学生将二次函数应用于实际生活时,可以通过如下措施开展教学。
一、构建函数情境,培养模型意识
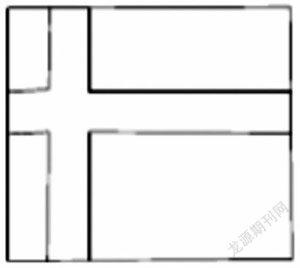
二次函数部分知识应用于生活情境中,要求学生对二次函数有一定的模型意识,要求学生将问题情境中的数值关系应用数值和字母表示出来,建立函数关系、建立二次函数模型,让学生学会将情境问题转化为数学问题。在函数与实际生活这一部分知识内容的教学中,有一例典型例题:如图所示,在长200米、宽80米的矩形广场内修建等宽的十字形道路,绿地面积y(m2)与路宽x(m)之间有怎样的关系?
在这一问题设置后,教师引导学生将图片中绿地的面积应用字母和数值表示出来,并通过矩形面积求解的方式建立函数关系,情境问题也就转化为数学问题。在解答这一情境问题的过程中,教师要求学生独立分析并用函数关系表示。在课堂中,部分学生是应用边长关系将情境问题转化为函数问题的,用(200-x)m表示矩形绿地的长,用(80-x)m表示矩形绿地的宽,此时矩形绿地的面积y=(200-x)(80-x)(m2)也就得以建立。在这一情境问题的设置中,学生学会了应用字母和数值建立等量关系,模型意识逐步得以建立。另外,利润问题也是二次函数与实际生活这一部分知识的典型问题,应用字母和数值表示数量关系,将情境问题转化为数学问题,寻求利润最大化,这也是本部分内容教学的重点。一道典型例题如:某商店经营T恤衫,已知成批购进时单价是2.5元.根据市场调查,销售量与销售单价满足如下关系:在一段时间内,单价是13.5元时,销售量是500件,而单价每降低1元,就可以多售出200件.设销售单价为x(x≤13.5)元,所获利润为y元.那么
(1)销售量可以表示为
(2)销售额可以表示为
(3)所获得的利润可以表示为
在如上问题设置后,教师循序引导学生将情境中的隐藏条件挖掘出来,引导学生应用字母和数值表示销售量、销售额和利润,函数模型得以建立。
二、应用函数性质,求解实际问题
在情境问题的求解中,二次函数的性质和二次函数的图像是辅助学生求解实际问题的重要工具,实际问题的求解也是帮助学生巩固对二次函数性质的重要过程。对此,教师可以在学生建立模型意识之后,应用二次函数求解实际问题。如上文中提出的面积问题中,当学生建立了y=(200-x)(80-x)(m2)这一函数关系之后,教师引导学生将函数解析式写成标准形式:y=x2-280x+16000。此后,教师引导学生求解绿地面积的最大值及其对应路的宽度时,也就将问题转变成求解二次函数的顶點问题,其中的路的宽度就是自变量x的取值,因变量y的最大值则是绿地的最大面积。再比如,在上文中的利润问题中,当学生应用字母和数值表示出二次函数关系(y=-200x2+3700x-8000)之后,教师引导学生结合问题情境求解出利润的最大值,问题也就转变为求解这一开口朝下的函数的极值问题,销售单价也就是成为求解函数极值问题中所对应的自变量x的值的问题。通过生活化问题情境转化为函数关系之后,教师引导学生求解最大值、最小值问题时,情境问题中提炼出来的函数解析式也就成为了考察学生对二次函数性质理解的重要资源。
在二次函数与实际生活这一部分的知识中,求解情境问题的步骤也就是从生活情境中提炼数量关系并构建数学模型,在模型建立之后利用二次函数性质求解函数值的问题。按照这一步骤,教师在新授课中引导学生按照这一顺序和步骤完成这一部分新知的学习,学生的解题能力也就逐步得以提升。
总结
二次函数是初中阶段数学学习的重点,也是学生学习的难点。融合了实际问题的二次函数部分的学习,综合性更强、对学生对二次函数部分知识的理解更深。对此,教师在教学中便可以通过构建函数情境以培养学生模型意识、应用函数性质以求解实际问题的方式引导学生展开学习活动,帮助学生体验函数知识在实际问题的求解中所带来的便捷性和高效性,让学生的思维能力从二次函数生活问题的训练中得以提升。
[ 参 考 文 献 ]
[1]林玉镰.初中数学二次函数教学研究[J].名师在线,2019(21):71-72.
[2]王淑琴.初中数学中“二次函数”的教学策略初探[J].数学学习与研究,2018(13):125-126.
[3]王伟民,杨培军.“实际问题”不能脱离“生活实际”——对数学教科书中几个问题的商榷[J].教学与管理,2018(16):57-59.
