促进数学深度学习的教学策略举隅

张蕾萍

摘要：针对初中数学教学中出现的被动、孤立、机械的浅层学习而提出的数学深度学习，不仅强调积极主动的学习状态、知识整合和意义联结的学习内容、举一反三的学习方法，还强调高阶思维的发展和复杂问题解决能力的提升。促进数学深度学习的教学策略有：情境创设，应注重激发学生的认知需求;问题设计，应注重发展学生的高阶思维;意义建构，应注重知识的联系整合;能力提升，应注重过程的反思总结。

关键词：初中数学 深度学习 认知需求 高阶思维

黎加厚教授认为，深度学习是在理解的基础上，批判地学习新思想和事实，并将它们融入原有的认知结构中，在众多思想和事实间进行联系，并将已有思维、知识迁移到新的情境中，做出决策和解决问题的学习。针对初中数学教学中出现的被动、孤立、机械的浅层学习而提出的数学深度学习，不仅强调积极主动的学习状态、知识整合和意义联结的学习内容、举一反三的学习方法，还强调高阶思维的发展和复杂问题解决能力的提升。

促进数学深度学习的教学，要超越知识的表层符号，深入研究知识的发生、发展过程，创设激发学生认知需求的情境，设置有挑战性的问题，引导学生通过自主探究建构知识，促进学生将新旧知识相融合，将众多思想相关联，并有效地迁移知识、解决问题，进而实现由知识建构向能力提升的转变。

一、情境創设，应注重激发学生的认知需求

深度学习是基于已有的知识和经验，通过同化或顺应来建构新知识的过程。创设适当的情境可以唤醒学生的已有知识和经验，促使新旧知识发生冲突，引发问题，维持、强化、调整学生的学习兴趣，激发学生的认知需求，从而开启深度学习之旅。

（一）从数学外部问题出发创设情境

数学知识往往较为抽象，甚至枯燥，无法有效吸引学生的注意。因此，教学过程中，教师应注重依据素养培养目标、教学内容和学生的认知特点等，设置如生活实际、实物演示、图画再现、史料故事等生动直观、易于理解的数学情境，激发学生的学习动力。

例如，教学“同类项”时，将书本、粉笔、卡片、三角板等散落在讲台上，请学生整理，学生很容易用分类的方法整理好。同时，展示超市琳琅满目、错落有致的商品陈列画面，让学生感受到分类广泛地存在于生活中，并体会到分类的必要性。

再如，教学“轴对称图形”时，呈现一组图片并引导学生观察思考：根据图1中一半的图形，猜猜画的是什么？你们觉得图2中的图形美不美，它们有什么共同点？可以从哪儿将这些图形分为左边和右边？怎么才能知道这些图形左边和右边完全相同？这些从数学外部过渡到数学内部的问题情境，让学生从想象到体验、从学习到运用逐层深入，唤起学生强烈的求知欲望。

（二）从数学内部问题出发创设情境

从数学内部问题出发，在知识的易错点、交汇点处设置悬念，引发学生原有认知结构与新的学习内容之间的冲突，可以激发学生积极思考，引发学生主动探究，帮助学生迅速进入学习状态。

例如，教学“正弦、余弦”时，设计情境：（1）直角△ABC中，∠C=90°，已知斜边AB和一条直角边AC，如何求另一条直角边BC？（2）直角△ABC中，∠C=90°，已知∠A和斜边AB，如何求∠A的对边BC？对于情境（1），学生自然会想到勾股定理。而对于情境（2），学生会发现利用勾股定理无法解决，从而产生认知冲突，进而产生迫切的求知欲。

再如，教学“乘法公式”时，很多教师通过利用两种方法计算图形面积引入乘法公式，但是学生会生发“怎么知道计算这个图形的面积就能得到乘法公式”的疑问。学生做得到，但是想不到，就是“假探究”，不是深度学习。其实，多项式乘法是乘法公式的知识生长点：在多项式乘法（a+b）（c+d）=ac+ad+bc+bd中，若字母a、b、c、d有某些特殊关系，就有相应的乘法公式，如a=c、b=-d时有平方差公式，a=c、b=d时有完全平方公式。因此，乘法公式是多项式乘法的特例。“考察特例”是数学研究的基本“套路”，体现了从一般到特殊、归纳的思想。据此，教学“乘法公式”时，可引导学生先复习多项式乘法运算，再探究多项式乘法法则有哪些特殊情形，能够得到哪些特殊结论。这样的设计，切合知识发生、发展的过程和内在的逻辑线索，符合学生的认知规律;学生自主寻找特例，探究的空间大，是“真探究”，是深度学习。

二、问题设计，应注重发展学生的高阶思维

数学教学是思维活动的教学，而问题是思维的起点与动力。将教学的内容与能力要求设计成具有系统性和灵活性、环环相扣且层层推进的问题，能引导学生的思维由浅入深、由表及里，有效发展学生的高阶思维。

（一）设计递进性“问题串”

深度学习不是一蹴而就的，需要逐步深入。教学中，教师要从学生的“最近发展区”出发，设计由简到繁，由易到难，由具体、明确、封闭和单一到抽象、模糊、开放和综合的递进性“问题串”，促使学生不断深入思考，思维水平也由感知、记忆等较低层次向抽象与概括、判断与推理等较高层次不断提升。这样的“问题串”在知识教学和习题教学中有广泛的应用。

例如，教学“圆周角定理”时，设计如下“问题串”，引领学生经历类比、作图、观察、猜想、度量、验证、分析、论证、转化、归纳等活动，由感性到理性、由特殊到一般地探究圆周角定理，理解知识的发生、发展过程，感悟相应的数学思想方法，提升思维的深刻性。

问题1类比圆心角的结论（同弧或等弧所对的圆心角相等），同弧或等弧所对的圆周角相等吗？

问题2先画一个圆心角，再画同弧所对的圆周角，你能画多少个？所画的圆周角（的度数）与圆心角（的度数）有何关系？先猜一猜，再用量角器量一量，你有何发现？

问题3一条弧所对的圆心角只有一个，而圆周角有无数个，如何用你所学的知识来推理论证它们之间的关系呢？

问题4在你所画的图中，圆心与圆周角的位置关系有几种情况？

问题5当圆心在圆周角的一边上时，如何证明？

问题6其他的两种情况下，如何证明？可否转化为上述情况？

再如，教学“相似三角形的性质”时，设计如下“问题串”，从特殊到一般，不断放宽条件，引导学生在不同的情境中逐步迁移运用“相似三角形对应线段（高）之比等于相似比”这一性质及已有经验解决问题，促使思维不断走向深刻。

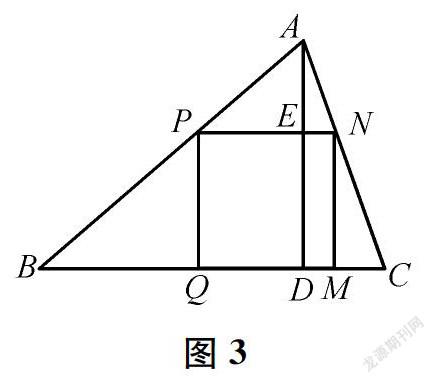
如圖3，有一块三角形余料ABC，边BC=120 cm，高AD=80 cm。要把它加工成正方形零件PQMN，使正方形的一边QM在BC上，其余两个顶点P、N分别在AB、AC上。

问题1加工成的正方形零件的边长是多少？

问题2如果原题中所要加工的零件是一个矩形，且长宽之比为2∶1，那么怎么加工，此矩形的面积最大？

问题3如果原题中所要加工的零件是一个矩形，那么此矩形的面积最大是多少？

（二）设计辨析性问题组

深度学习强调批判地学习新思想和事物。教学中，教师可从学生学习的易混点出发，设计既有联系又有区别、形似神非的辨析性问题组，促使学生自觉反思并发现学习过程和已有认识中的不足与错误，进行质疑、批判、完善和修正。

例如，教学“分式方程”时，学生遇到含待定系数的分式方程“无解”“有增根”等问题时，常常把它们混为一谈;遇到含待定系数的分式方程“有特殊解”的问题时，常常忽视增根。因此，设计如下问题组，引导学生在比较中辨析，在反思中完善和修正，发展思维的批判性。

分式方程需要去分母转化为整式方程求解。分式方程有增根即转化后的整式方程有解，但不是原分式方程的解，即原分式方程分母为0。分式方程无解包括两种情况：一是转化后的整式方程无解，二是转化后的方程有解，但相应的解是原分式方程的增根。即有增根是无解的一种情况。

题组1的三道题引导学生辨析“无解中的有增根”“无解中的有增根和无增根”和“无解即有增根”三种情况。题组2的两道题引导学生辨析“特殊解中包含增根”和“特殊解中不包含增根”两种情况。

三、意义建构，应注重知识的联系整合

数学知识之间是存在内在联系的。加强知识之间的联系与整合，有助于充分理解知识，灵活迁移运用，是深度学习的体现。教学中，教师需要引导学生发现所学知识之间的联系，从而对知识进行整合，使之条理化、系统化，促进学生进行有意义的知识建构。

（一）建立知识联系

数学各部分知识在内容上、方法上是相互渗透、纵横关联的。教学中，教师既要注意知识间的横向联系，又要注意知识间的纵向联系，从而设计好相应的“先行组织者”，引导学生进行有意义的学习，不断扩充和丰富已有的知识和经验，做到举一反三、触类旁通。

例如，教学“矩形、菱形、正方形”时，提出以下问题：学习平行四边形时，你积累了哪些研究经验和策略？你觉得可从哪些角度来研究矩形、菱形、正方形？引导学生类比迁移研究平行四边形的方法，从边、角、对角线等角度来探究矩形、菱形、正方形的特殊性质。

再如，教学“二次函数”时，提出以下问题：（1）一般从哪些方面研究函数？（2）根据研究一次函数图像与性质的经验和策略，你觉得应如何研究二次函数的图像与性质？第一个问题引导学生根据一次函数、反比例函数的学习经验概括函数研究的一般思路，即从函数的概念、图像、性质以及应用等方面来研究，让学生知道“学什么”。第二个问题引导学生类比研究一次函数从y=kx到y=kx+b、从k>0到k<0的思路来研究二次函数，即从y=ax2到y=ax2+k、y=a（x+h）2 再到y=a（x+h）2+k、y=ax2+bx+c，从a>0到a<0，研究图像的形状、位置、增减性以及位置关系等。

（二）发展认知结构

教学中，教师还要注意引导学生把不同的知识片段和模块联结起来，整合成有序的认知组块，发展出完整的认知结构。

例如，教学完《中心对称图形——平行四边形》一章后，教师可以指导学生小组合作绘制思维导图（如下页图4），将相关知识结构化组织、模块化架构和网络化呈现，发展学生的认知结构。

四、能力提升，应注重过程的反思总结

学习反思是对学习活动进行审视、分析、评价、调节的过程，有助于学习的真正深入以及对内容的本质理解，发展元认知，提升学习能力。教学中，教师要及时引导学生反思总结自己的学习过程。

一方面，知识教学中，教师要引导学生反思知识探究的过程，提炼获取数学知识的思想方法和有效策略，提高获取知识的能力。如，教学“圆周角定理”时，探究得出“圆周角的度数等于它所对弧上的圆心角度数的一半”后，教师要引导学生反思获得这一结论的探究过程，提炼相应的数学思想方法：猜想结论时，将直观操作和逻辑推理有机结合;论证结论时，先通过画图探究圆心与圆周角的关系有几种情况，体现了分类思想，再通过添加辅助线将“圆心在圆周角内部”“圆心在圆周角外部”这两种情况转化成“圆心在圆周角边上”的情况，体现了化未知为已知、化复杂为简单、化一般为特殊的化归思想。

另一方面，习题教学中，教师也要引导学生反思问题解决的过程，提炼问题的类型、特征以及解决问题的思想方法和有效策略，并思考问题的推广与变式以及解法的普适和优化，提升解决问题的能力。如，解决问题“如图5，在△ABC中，∠ACB=90°，AC=6，BC=8，AD是∠BAC的平分线。若P、Q分别是AD、AC上的动点，则PC+PQ的最小值是”后，教师要引导学生反思解题过程：这是“已知两个动点P、Q（分别在两条直线上）和一个定点C，求有关的两条线段长PC、PQ的和的最小值”的问题，只要将一个动点Q看成定点，就可以转化为比较熟悉的“两定点（直线外）、一动点（直线上），求距离和的最小值”的问题，即将军饮马问题，就可以通过找对称点实现“折转直”，再利用“垂线段最短”来解决。由此，让学生充分体会化陌生为熟悉的转化思想。

参考文献：

[1] 王宝斌.基于“问题链”，发展高阶思维——以化学教学为例[J].教育研究与评论（中学教育教学），2016（12）.

[2] 王弟成.引导探究，强调思想——对《椭圆的几何性质》一课的点评[J].教育研究与评论（中学教育教学），2017（12）.

[3] 〔美〕D.P.奥苏伯尔，等.教育心理学——认知观点[M].佘星南，宋钧，译.北京：人民教育出版社，1994.