以一次测试反观初中数学概念教学
2019-09-10张鑫
张鑫
摘要:本轮课程改革以来,初中数学的教学内容对概念进行了淡化处理,一定程度上避免了学生死记硬背数学概念的低效行为,减轻了学业负担,利于师生将更多的精力投入到数学核心素养的培养与提升之中。但对概念内容的淡化导致了部分教师弱化概念的教学及其应用,教学基本功不扎实并产生了不良后果。基于此进行的测试结果显示,学科基本功还需从多方面加以夯实。
关键词:初中数学;概念应用;教学方法;基本素养
数学是由概念、定义、公理、定理等组成的逻辑体系,数学概念是反映思考对象空间形式和数量关系本质属性的思维形式,是数学逻辑体系的基石。定义是揭示概念内涵的逻辑方法,是明确概念的主要方法之一。因此,概念既是学生学习数学思维形式的载体,又是学习数学逻辑方法的载体。明确概念的方法不唯一,给某一概念下定义的具体内容也不止一种。因此,概念本身远不如借助概念的应用来强化数学的思维形式和逻辑方法更有意义。
我们分别对32位初中数学教师进行了概念应用基本素养的摸底测试,题单如下,为闭卷笔试(其中有7人是通过网上教研的形式进行测试的)。

(一)求解部分


(二)讲解部分
此题的讲解部分设置了两处采集点。
第一处采集点是教师的讲解思路是否完整。本题完整的讲解思路可以参照初中数学解题流程图(如图1)进行,先明确概念“单项式”与“完全平方式”,再基于完全平方式的特点与题中所给代数式的差异,明确需要采用分类讨论的解题策略,进而确定分类标准,然后具体求解、验证。

第二处采集点是解题方法选择的分类标准是否精准。完全平方式是形如“a±2ab+b”的多项式,采用“将题中所给两项分别与完全平方式中的各项进行比对”的分类标准繁杂且容易导致混乱、遗漏(实际上是穷举法,本题中之所以有部分教师漏解即源于此因)。本题最为精准的分类标准是“题中给的两项与待添之项哪个是±2ab”。

基于前述評分标准我对八处采集点进行了数据采集,结果如图2所示。
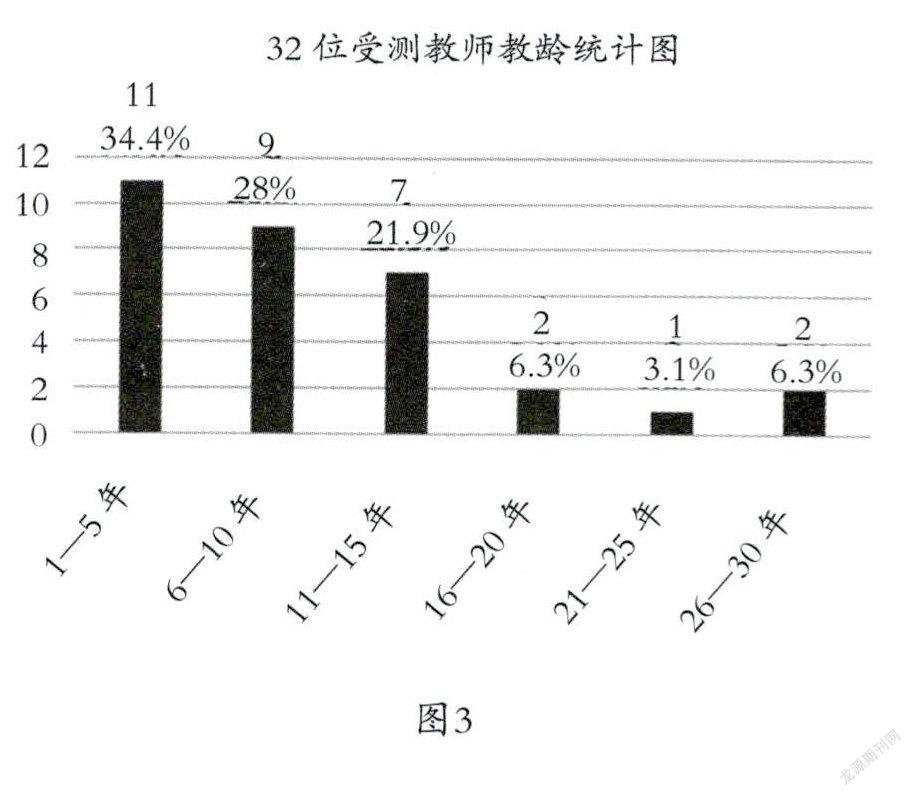
32位受测教师的平均教龄为9.6年,既有新人职的教师,也有市级名师和区级教研员,具体教龄构成如图3所示。
(一)部分教师对概念教学不够重视且缺少深入研究
数学概念是数学教学的基石,本次摸底测试的核心概念是“完全平方式”。尽管32位受测教师中分别只有6人作答时写了概念性错误答案“-1”和“4X”,但是其余教师在测后被问及“-1可不可以”时很纠结,基本说不清楚到底可不可以。基于此,本次调研对最后接受测试的6位教师在试卷背面进行了现场补充追问“添一1行吗”(不得更改正面已经作答的内容),数据采集结果如图4所示。其中,回答“行”的四位教师中,有一位教师在追问前就已经在正面书写了概念性错误答案“-1”和“4x2”,有两位教师自主补充了概念性错误答案“-4x2”。由此可知,尽管其中的5位教师在作答时没写概念性错误答案,但经过追问的诱导,有3位教师认为可以“添加-1”,占比60%。显然,全部受测的32位教师中,那26位没有写出这两个概念性错误答案的教师极有可能是因为“没考虑到这种隋况”而“躲过了雷区”。

完全平方式在北师大版初中教科书上是以图6的形式呈现的,很多教师结合上面的题目想到了“并没有明确a或6不为0”。他们还是基于数值本身来看待完全平方式的概念,却没有看到此概念是以类差来定义的——“形如a±2ab+b”,导致他们没能从形的视角来看待完全平方式的概念。有的教师认为“-1或-4x”可以使“4x2+1”转化为“4x2”和“1”,是完全平方数。实际上,由于题目对字母的取值并未明确界定,因此“4x2”并不一定是完全平方数。而且,完全平方数与完全平方式是两个不同的概念。

图5中所示的北师大版教科书内容是采用了“种加类差”的方式给完全平方式下的定义。“种”是“式子”,“类差”的是“a±2ab+b”。部分教师的困惑之处在于教科书所给定义的“种”和“类差”都相对宽泛——“式子”的外延既包括多项式,也包括单项式和分式;“a±2ab+b2”中字母的取值并没有像函数、方程的定义那样进行明确的限定“k≠0”“n≠O”。
如图6,人教版教科书对完全平方式的定义相对明晰。从思考问题到定义前均有“多项式”的文字表述,算是进行了概念的限制。据此可知“如果a或6的值为0时,原式将转化为a、b或0,均是单项式,不符合完全平方式的定义”。

顯然,部分教师既缺少对教科书上数学概念的深入剖析,又缺少不同版本教科书对同一概念的比对,从而无法深入理解概念,导致概念教学难以达到应有的效果。
(二)部分教师对讲题时的思路剖析缺少必要的规范
讲题的一个重要目的是触类旁通,需要剖析题目的知识点、思路的源头、对策的选择等,从而引导学生学会解答一类问题,而非仅停留在“听懂此题”的层面。本次对教师进行摸底测试的题目是一道基于概念且考验思维广度和深度的代数题目,因此概念剖析至关重要。因为本题要求添上的是单项式、得到的是完全平方式,所以首先就应该引导学生进行概念辨识何为“单项式”、何为“完全平方式”,再通过比对完全平方式的数学模型感知“需要分类讨论”这一思路源头,进而为“采用怎样的标准进行分类”想对策。写了概念性错误答案的6位教师中,只有3位教师设计了完全平方式的概念复习或模型再现。
(三)部分教师对解题时的方法选择缺少必要的研究
分类讨论的难点是分类标准的确定,好的分类标准能化繁为简,事半功倍。对于本次摸底测试中的题目,如果采用“谁是完全平方式模型中的a、±2ab、b”来对位讨论,将导致需要的思维量大增,事倍功半,甚至导致错、漏。完全平方式中的“平方项”有两个,而“2倍乘积项”只有一个。因此,应该用“2倍乘积项”作为分类标准来简化运算。从教师的作答情况来看,本次摸底测试中只有2位教师答出了3个正确答案,只有l位教师选用了简化的标准(却出现计算失误),而其余教师只是知道需要分类讨论,但对于分类讨论的标准却是跟着感觉走的,更像是“穷举法”,劳而少功甚至无功。
(一)练好概念教学基本功
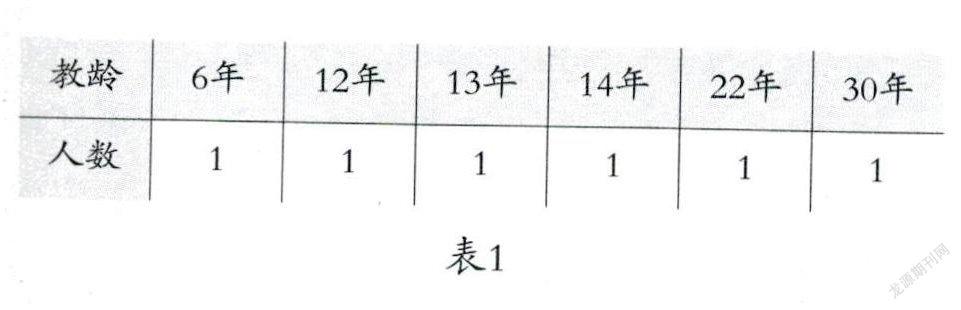
从32位受测教师的教龄数据来看,平均教龄为9.6年,教龄在1至15年的有27位教师,占受测教师总数的84.4%。12人次的概念性错误答案“-1”和“-4x2”集中于6位教师,其教龄统计见表1,平均教龄位16.2年。
尽管受测教师的教龄区间与本轮课程改革的全程基本重叠,似乎能够说明本轮课程改革淡化概念的影响。但事实上,其教龄在16~30年的5位教师中,完全写出了全部概念性错误答案的有2位,占这一教龄区间的40%,占全部写出概念性错误答案的6人中的33.3%。32位受测教师中有5位教师出现了形如“+1/16x”的概念性错误答案。此种情形的错误貌似触碰了“添一个单项式”的概念红线,但更像是受测教师被困于“因分类标准不精准导致分类讨论的实施与结果过于复杂”而忽视了题目要求“单项式”。其实,本题的题干只须“添一项,,即可,而“添一个单项式”中的“单项式”是冗余的已知条件,算是题目对受测教师的一个善意提醒。可见,上述5位教师因为概念教学的弱化而没能接收到这个的信息。这也印证了很多受测教师的解题基本功也不够扎实。
显然,上述测试结果与本轮课程改革对数学概念的淡化之间的因果关系并不明确,但部分受测教师的概念教学不扎实、解题方法不当等教学基本功不理想的弱点却是暴露无遗的。
实际上,本轮课程改革淡化的是概念本身,而不是概念所涉及的思维形式和逻辑方法。

1.概念教学应该明确概念之间的关系
完全平方式与其上位种概念之间的从属关系如图7所示。对可比较概念之间从属关系的揭示能很好地助推学生深入理解概念以及概念体系,同时也利于渗透数学概念之间的逻辑关系和数学的思维形式。
2.概念教学应该突出概念的主要特征
“类差”“形如a±2ab+b”既将完全平方式从其种概念中剥离了出来,又将抽象的数学概念具象化了,这样就使概念本身又多了易为接受的鲜活的一面,也直观地展示了完全平方式这一概念的外延。同时,对概念内涵与外延的揭示能让学生站在数学的“基石”上思考、解决数学问题而不受诸如本次测试中概念性错误答案“-1”和“-4x”的迷惑。
3.概念教学应该突出概念的主要词句
“多项式”既是完全平方式这一概念的“种(上位)概念”,也是这一概念的关键词。借此便能“越級”将与完全平方式上位概念具有矛盾关系的概念“单项式”区分开来。但是,北师大版教科书与人教版教科书所给出的完全平方式的定义中都将关键词落在了“式子”上,这是不利于学生准确把握完全平方式的概念的。因此,教师要大胆处理,借用人教版完全平方式的“前言”迁移“多项式”这一关键词来澄清疑惑。
4.概念教学应该突出概念的新旧对比
学生们在学习完全平方式之前学习过完全平方数的概念,而具体的完全平方数是一个具有特殊性的数,但具体的完全平方式却是一个三项多项式。这种显著的差异所带来的认知冲突需要经历一个顺应的过程才能纳入学生的认知体系。因此,概念教学要注意做好新旧概念的对比,助推学生理清概念间的异同,以便更好地把握概念本质。
5.概念教学应该突出概念的灵活运用
学以致用,唯有用才能深化学的结果。让学生经历初步的概念辨识后,就可以由浅入深地投送一定数量和难度的题目考查学生概念掌握的扎实性和思维的灵活性。以本次调研所用的题目为例,可以通过“搭梯子”的办法通过问题串来引导学生夯实完全平方式的学习:代数式缸2+1是不是完全平方式?如果是,请说明理由;如果不是,请做出适当的改变使其成为完全平方式。
(二)夯实学科教学基本功
1.力口强学科课型的研究
按教学内容可以将初中数学学科的新授课基本课型划分为概念课、命题课和应用课三类。每类课型的教学目的任务、课型特征、教学策略、教学基本结构和课堂优化标志不尽相同,教师要研习相关理论与文献,借鉴已有教科研成果积极实践。
2.力口强解题方法的研究
解题后要反观解题过程,思考是否还有其他解题方法,并比较不同方法的优劣;要对解题过程进行剖析,提炼解题思路、归纳解题经验、归因解题教训;要归类典型题型,力争梳理出学科题型体系,提升对学科认识的系统性。
3.加强讲题规范的实践
讲题时要注重以一道题带动一类题,从审题时的知识点识别,到思路的起点、节点、归纳及变式训练,在实践中培养学生解题时思考过程的科学性和规范性。但也要注意解题的灵活性,不要形成思维定势死记硬背模式化。
虽然造成上述问题的原因是多方面的,但很多教师无暇研习是一个重要的因素。集体备课既需要指出教学要面对的难点和易错点,更需要深入思考、研讨解决问题的策略与方法,要深入到教法、学法以及学法指导的层面,要落实到焦点问题的教学实践中,这些内容均需要相对充分的时空保障。在加强集体备课、集思广益的同时,教师自身也应该通过自测等形式做好基本功提升和拓展研修的工作,从而更好地落实课程改革的新理念、探索课程改革的新方法。基于上述调研分析,淡化概念不是淡化概念的教学及其应用的教学基本功。在本轮课程改革的大背景下,一线教师仍需夯实教学基本功,在实现专业发展的同时,让学生成为本轮课程改革的最大受益者。
