我们为什么要提问

摘要：这学期，尝试让学生提问。久而久之，问成了习惯，学生已经不满足于向书本提问，课上也开始相互提問，以至于发展到要向老师提问的程度了。反问自己为什么要提问，目的在于了解真实的学生，激发自然的学习，体会思维的力量。

关键词：提问真实学习思维

“为什么要提问？”这个问题不是我问出来的，是一个学生在记事本上给我布置的作业，还颇为贴心地留下了解答的地方。

我一边习惯性打勾，一边写下“面谈”二字，心想：小朱同学你厉害啊，已经把问题提到老师这里来了，还摆出一副非答不可的架势，牛！其实还是挺高兴的，估计小朱同学这问题，就是这学期，被每天必须提若干个问题的作业给逼出来的。

说起这学期让学生提问的事，也是从照猫画虎开始的。上学期，老纪来我们这里上了一节QCC（Q，即question，提问;C，即conversation，对话;C，即collaboration，合作）语文课，从学生的问题出发，展开语文学习，深入进行思考。这个思路让我大受启发。数学能不能也QQC一把？

结果，这学期开学没多久，QQC数学创始人老杨就来传经送宝了。老杨说，她的数学课，学生能提出很多问题，而且就提在数学书上。说着，还顺手展示了一位学生书上的一大串问题。《用量角器量角》这课，学生就能问出：量角器为什么是半圆形的？为什么平均分成180份？为什么用“°”表示度？怎么量出多少度……

当时，我真是既惊讶又惊叹。

数学书和语文书不同，研究过程、思考方法甚至最后的结论都是明明白白写在那里的，让学生把书都看了，还提啥问题啊？但事实摆在那里，老杨的学生不仅看了，还问了，问的问题还很有想法，学习中的重点和难点都让他们问出来了。

我的学生能提出问题吗？会提出什么样的问题呢？心动不如行动，新的一学期，从第一单元《等式和方程》开始，提问！

一开始没敢让学生在书上提问，一是担心学生看了书，就提不出什么问题，自己也觉得这单元好像没什么好问的;二是担心万一学生有了问题，是解决还是不解决呢？也不知道怎么处理才好。索性，先提在研究单上。

学生的问题倒是挺多。不过，牢骚也多。那阵子，学生在我耳边说得最多的就是：我已经绞尽脑汁了！我真的尽力了！我已经使出洪荒之力了！老师，您饶了我们吧，真的是再也提不出问题了！

为了鼓励大家积极提问，其实也是为了安抚学生面对强制性提问的不适，我让他们选择自己觉得有意思的问题，写在小卡片儿上，署上名字，贴在班级的板报墙上，美其名曰：问题墙。

到了第二单元《折线统计图》，问题干脆就提在了书上。有了书做支撑，学生的问题好像被“开了闸”，源源不断。

本来，我就想找两个无关大局的小单元试试，就想看看，老杨说的那个情况，是不是不可复制的个例。但做着做着，不仅是我，就连学生都有点上瘾了。于是，提问就成了学生在每个学习阶段都做的常规作业了。

或者说，提问成了一种习惯。学生已经不满足于向书本提问，课上也开始相互提问，以至于现在，发展到要向老师提问的程度了。而我又没有和学生明确地解释过为什么要提问，有此一问，实属正常。

那么，为什么要提问呢？我也在问自己。

一是了解真实的学生。

学生的学习，是怎么开始的呢？是从教师的问题开始的。教师的这些问题又是怎么来的呢？很多时候，靠的是经验，是感觉，或者说是猜。

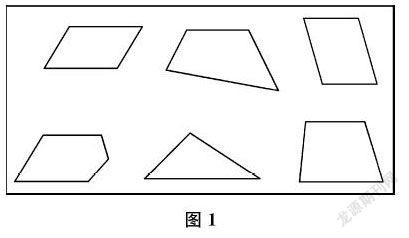
一个是从教材的维度猜。这节课认识平行四边形，教材需要学生认识平行四边形边的特点，我们就可以设计这样一个问题：观察图1中的这些图形，哪些是平行四边形？它们的边有怎样的特点？

一个是站在学生的角度来猜。这节课研究除数是整十数的除法口算，学生计算60÷20，会怎么想呢？根据经验，要么想乘算除，通过20×3来算60÷20，要么想6÷2，推理60÷20。那就在这里设置问题：60÷20，商是几？你是怎么想的？

但其实，学生已经知道了什么，能继续探索出什么，还想知道什么，有什么不清楚不明白的地方，我们真的知道吗？

其实，我们真的不敢轻言知道。

之前，我们的团队就一直在做大问题引领下的前置学习的研究，精心设计研究问题的时候，我就常常选择困难：这个问题合适吗？学生真的需要研究这个而不是那个问题吗？什么样的问题才是能调动学生深入思考的问题？这是因为，我缺乏途径来了解学生，了解他们对学习内容的真实感受和实实在在的问题。目前来说，无论教学形式如何转变，几乎所有发问的权利都还牢牢控制在教师的手里。

但你看，当学生开始提问后，即使他们还非常拘谨，还在试图揣摩老师让他提问的意图，但他们对未知好奇的天性，对不能认同事物的疑惑，还是会驱使他们先问为快。

他们讨厌烦琐的方程格式，就会拐弯抹角地问：有了方便的算数，为什么还要学方程？

他们觉得课本下面那一行小小的字，“研究因数和倍数时，所说的数一般指不是0的自然数”，硬生生取消了自然数“0”的话语权，于是讨论：一个数的因数和倍数，为什么不能有0？分数、小数为什么也没有自己的因数和倍数呢？

关于质数合数、奇数偶数，总觉得它们难分难解，于是会像绕口令一样问出：奇数会是合数吗？一定是质数吗？偶数和合数是什么关系？有没有偶质数？奇合数？

其他的自然数不是质数就是合数，可1什么也不是，于是很不甘心：1就不能也起个名字吗？

实话实说，阅读这些问题的时候，我的情绪波动很大，激动有之，那是问到了教学中的关键处;大笑有之，那是看到了学生特别稚气的一面;困扰有之，因为有些问题连我也不知道该怎么解决。

不过，解决问题是以后的事情。能让学生打开心扉，提出真实的问题，这本身，就已经让我们离学生又近了一步，让我们了解学生又多了一条路径，不是吗？让学生提问，可能是一种最为直接、方便的“备”学生的方式了。

二是激发自然的学习。

前文说，在学习中，大部分都是老师在提问，学生在回答老师的问题。似乎学习的事情，理应如此。指望学生搞明白学习的方向，问出学习的关键和难点，那还要老师做什么？

但是，问题出自于谁，真的是个很严肃的问题。

爱因斯坦说，提出一个问题往往比解决一个问题更为重要。他后面还有一句注释：因为解决问题，也许仅是技能而已，而提出新的问题、新的可能性，从新的角度去看旧的问题，却需要创造性的想象力，而且标志着科学的真正进步。

爱因斯坦给提问定的调很高，直接上升到科学进步的高度。谁说不是呢？但我的想法可能更简单一点，谁提出的问题，表明谁真的对这个问题感兴趣，谁真的在意这些问题有没有得到解决。

教师为什么要备课堂上的问题，那是他需要学生解决这些问题，因为这些问题就是教师所理解的教学中的重点和难点。教师是最关心这些问题是否解决的人。学生呢，只需要解决老师的问题，所以常常在教学中，有一种你拼命地问，他却岿然不动的状态。

如果情况翻转过来呢？学生真的迫切想知道什么的时候，会是什么样的情况呢？

举个例子，儿子有天吃饭的时候问我，“黑洞和虫洞有什么区别？”我第一反应就是，这什么问题啊！接着就想，就算我能说明白，你能懂？还有，现在要知道这些干吗？还好，我忍住了，说：“这问题，妈妈还真不知道，也从没有想过。”谁知道人家早就等在那里，“你查一下百度啊，谁让你回答了。快查！”好吧，我查着百度，看着满屏的文字，实在是没兴趣和他一起看下去，但儿子足足研究了一餐饭的时间，还点开了几个相关的链接，甚至找到了几个百科视频，连我都觉得有点儿兴趣了。最后，他满足地说：“嗯，一个是个天体，一个是一座桥。”我感觉他说得还挺在理。

你看，同一个问题，问的人总是更有兴趣知道答案。

再举个例子，我们最近在学习质因数和分解质因数。学生对这些问题都很感兴趣：有了质数和因数，怎么还有个质因数？三个名称间到底是什么关系？最后讨论的结果是，整合成一个大问题：质因数是什么？自己回去研究。

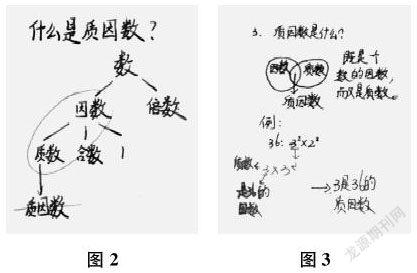
学生的研究非常有意思，文字表述的，举出例子的，还有各种图示，一类是枝状图（如图2），一类是集合图（如图3）。书本解释得很到位，但因为是大家共同的问题，课前都有自己的思考，于是，交流也同样激烈。

“第一幅图，我觉得根本就不需要再写上质因数，这里圈起来，就能表示出什么是质因数。”“第二幅图，我觉得不对，因数是相对的，而质数是能独立存在的，这两个画成集合圈不合适。这样感觉质因数也可以独立存在了一样，它也应该是相对的。”

有人说，无问题不学习。虽然有点绝对，但有问题，更容易激发学生去研究、去探索、去思考。好奇心，是人类探索未知的无穷动力，正是在问题的不断驱动下，学习才能成为一种自然而然的需要，一种来自心灵的需求。

三是体会思维的力量。

首先，学生在不断体会思维是有力量的。他们要提出问题，就需要观察、阅读、思考、分析。一道例题、一张图片、一段文字，过去学生是不读的，有时候你让他读，也读不出什么信息来。因为，没有认真读的需要和理由。现在不同了，要提问，就得仔细读，认真比较，拿出十二分的劲头来分析，要不断搞明白：什么问题问了等于没问，答案是很容易获得的;什么问题才能算是真问题，问了以后大家会感兴趣，觉得你很厲害。这个过程，他不仅要分析，要决策，还要自我批判。

同样，在课堂上，听了别人的问题，要理解，要做出判断，要给出自己的意见，这就得很认真地听，思维活动的质量决定了一个人在交流中的位置。

为了真的能听到、听懂，学生会一声不吭，站起来听，跑一圈到跟前去听、去看。最后讨论出的问题，会成为他们共同研究的问题，这种感觉很奇妙，尤其是还有署名权（后来为了更方便记录，改成了学号），特别有荣誉感。

其次，是教师自己也在不断体会思维的力量。看着我的学生，争先恐后地要说出自己的问题、进行解释、讨论问题价值的时候，我觉得能让一个人真的思考起来，是一件令人热血沸腾的事情。

我看着学生自制的、密密麻麻、图文并茂的问题研究单，觉得每一张都应该珍视，要让这些闪亮的思维火花都有绽放的机会。

于是，在解答了小朱同学的问题后，还让全班也花了5分钟，即兴表达对“为什么要提问”的思考。

一直相信，没有哪一种学习方式是最完美的，我们都在追寻完美的路上……

（吴贤，江苏省南京市北京东路小学校长助理，南京市玄武区小学数学学科带头人。）