体验数学文化 实现教学目标

洪建龙

[摘   要]以“三角形的内角和”的教学为例，先引导学生回顾泰勒斯的基本拼图方法、挑战泰勒斯拼图方法，在此基础上提高难度，引导学生继续挑战，从而让学生自主探索与发现，多角度和多样化地解决问题，实现知识的自我建构，掌握科学研究的方法，形成实事求是的科学探究精神，同时感受数学文化的魅力.

[关键词]数学文化;教学目标;三角形的内角和

[中图分类号]    G633.6        [文献标识码]    A        [文章编号]    1674-6058（2019）20-0022-02

“三角形的内角和”是人教版教材八年级上册第十一单元的内容，属于“空间与图形”的范畴，是在学生已经掌握了三角形的稳定性和三角形的三边关系相关知识后对三角形的进一步研究，主要验证“三角形的内角和等于180°.教材中安排学生对不同形状、大小的三角形进行度量，再让学生运用拼、折、剪等方法及通过观察、猜想、实验、验证等数学活动，探索发现三角形的又一特性——三角形的内角和等于 180°.学生在探索过程中体验了发现的乐趣，发展了推理能力，感受到了数学文化的魅力，增强了学好数学的信心;学生在动手获取知识的过程中，培养了创新意识、探索精神和实践能力.采用探究式教学，可让学生在开放的学习过程中，自主进行探索与发现，多角度和多样化地解决问题，从而实现知识的自我建构，掌握科学研究的方法，形成实事求是的科学探究精神.

一、 回顾泰勒斯的基本拼图方法，了解定理起源

回顾泰勒斯最基本的拼图方法，了解发现三角形内角和定理的起源.

方法1：准备六个全等的三角形，利用它们动手拼图，讨论交流，得出拼图结果.如图1所示，三角形的内角的顶点重合，并且顶角不重叠地拼在一块，拼成一个周角（360°），三角形的每个顶角各出现两次.则：

教师：大家很厉害！重新发现了古希腊数学家泰勒斯曾用过的方法.当年，泰勒斯就如大家一样，用六个全等的三角形拼图，拼成了一个周角，从而发现了三角形的内角和为180°.大家还原泰勒斯的三角形拼图方法.真是英雄所见略同.真的了不起！

二、 挑战泰勒斯拼图方法，掌握定理

针对泰勒斯用六个全等的三角形拼图发现三角形内角和定理，教师向学生提出任务：挑战泰勒斯拼图方法.

教师：为了解释三角形的内角和为180°，泰勒斯用上六个全等的三角形，实在是太多了，如果用三个同样的三角形拼图，大家能完成吗？

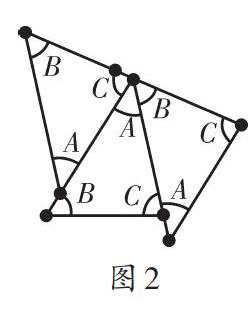
全体学生积极响应，大家使出浑身解数，苦苦思索，尝试拼图.忽然，有学生发现，图1（a）去掉上面一半，剩下部分表明三个同样的三角形照样能拼得三个内角的和为180° .于是学生尝试应用三个全等的三角形进行拼图，如图2、3、4、5，得出精彩的结果.教师一一展示学生的拼图作品.

如图2、3、4、5，三角形的内角顶点重合，并且顶角不重叠地拼在一块，拼成的图形中，三角形的每个顶角各出现一次，刚好摆成一平角（180°），所以 ∠A+∠B+∠C=180°.

教师：数学家泰勒斯曾用六个全等的三角形去拼图，而你们只用三个全等的三角形拼图就能说明三角形内角和定理，真是青出于蓝而胜于蓝！

教师要求学生继续观察图2、3、4、5，思考图3、4、5中有什么相等.

学生通过讨论得出：图形中有角相等，并且还是内错角，由此得到平行线.图3、4、5提示：过点A作辅助线DE平行BC，利用内错角相等，从而把角B、C移到上面而构成一个平角，不难得到三角形的内角和定理.

教师：利用三个全等的三角形把三个内角拼成一平角，实现拼图解读三角形内角和为180°.我们找到的这种拼图法，也非常简洁，它最早由古希腊数学家泰勒斯发现.

点评：利用三个全等的三角形去拼图已经给学生机会去进行数学创新，体验创新;并且还进一步让学生去发现证明三角形内角和定理的辅助线方法，同时，也给學生作辅助线提供了一个基石，开阔了学生的眼界，丰富了三角形内角和的内涵.

三、提高难度，继续挑战

泰勒斯用三个全等的三角形进行拼图去解释三角形内角和定理，其实数学家帕斯卡少年时只用一个三角形就说明了三角形内角和定理.教师利用这个案例激发学生思考的热情，培养学生的数学思维，加深学生对三角形内角和定理的理解和掌握.

教师：泰勒斯用六个或三个全等的三角形拼图，你们能只用一个三角形说明三角形的内角和为180°吗？

教师的提议立即得到学生的响应，学生纷纷思考、讨论起来，有的学生说没办法拼图，有的学生看到别的同学将三角形纸片折来折去，于是得到启发：既然无法拼图，那就进行折纸.于是，就有了如下创新：

方法1：如图6的三角形，把上面的角沿虚线横折，使它的点落到底边上，再将剩下的两个角横折过来，使三个角正好拼在一起，这样三个角就组成了一个平角，所以可得出结论：三角形的内角和是 180°.

方法2：如图7，作三角形三个内角的角平分线，交于一点O，将三角形的三个顶点对准交点O折叠，折过来得到三个角A、B、C，还有三个空白部分，正是三个角∠A、∠B、∠C的对顶角，大小正好等于∠A、∠B、∠C，则有2∠A、2∠B、2∠C刚好围成一个周角，即2∠A+2∠B+2∠C=360°，于是  ∠A+∠B+∠C=180°.

教师：大家的方法非常新颖.不过，这两种方法，帕斯卡在12岁时早已发现.他的父亲得知他利用对称巧妙进行拼图，独立地获得三角形内角和定理时，激动不已，当即解除对他数学学习的禁令，让他可以阅读任何数学书籍.自然，后来帕斯卡成为法国著名的数学家、物理学家、哲学家.尽管你们是重新发现帕斯卡的方法，但你们也算创造性地运用了这一方法，独立地发现了三角形内角和定理，非常了不起！

教师：还有别的办法吗？

学生又给出了方法3.

方法3：取△ABC两边AB、AC的中点D、E，如圖8，过中点D、E作第三边的垂线，并沿垂线剪下，得两个三角形，把这两个三角形依图形补上，得一正方形（如图9）.三角形的三个内角刚好拼成一平角.于是  ∠A+∠B+∠C=180°，说明三角形的内角和等于180°.

点评：剪三角形将三个内角拼成一平角，方法仍然巧妙，开阔了学生的视野.由三个全等的三角形拼图到只用一个三角形，同样能说明三角形内角和定理，是一个大挑战，但学生仍然创造性地解决了问题，这对于培养学生“直观想象”核心素养、发展学生创新思维具有极高的价值.

四、 挑战帕斯卡，不拼也不折

由六个全等的三角形、三个全等的三角形拼图，再到只有一个三角形在拼、折中发现、解释三角形内角和定理，难度越来越大，但问题解决得越来越精彩.教师提出问题：若不折、不拼还能发现、解释三角形内角和定理吗？比如，旋转一支笔，能发现三角形内角和定理吗？ 许多学生感到很疑惑，用一支笔如何能说明三角形内角和为180°？他们用笔比画着，绞尽脑汁，师生共同关注，一起交流，最终比画出三角形内角和定理.

方法：如图10，学生将BC上的笔的笔尖指向点C，绕B点沿逆时针方向旋转角度B，与BA方向一致，笔平移到笔端与点A重合，绕BA上的笔尖点A逆时针方向旋转角度A，与AC重合，笔平移到笔端与点C重合，绕此点C逆时针方向旋转角度C，笔尖指向点B，与CB重合，与刚开始的笔尖指向点C比较，笔已转过180°，恰好是三角形三内角的和，这样说明了三角形内角和定理.

教师：同学们做出了德国数学家提波特的精彩作法.1809年，德国数学家提波特利用旋转的方法证明了三角形内角和定理.如图10，将AB所在的直线[xy]绕A沿逆时针方向旋转角度A，到AC所在直线[x′y′]，将[x′y′]绕点C沿逆时针方向旋转角度C，到BC所在直线[x″y″]，最后[x″y″]绕B沿逆时针方向旋转角度B，到AB所在直线[x?y?]，从[xy]到[x?y?]，总共转过180°.

点评：三角形内角和定理的发现、解释，方法巧妙，精彩纷呈，只要指点得当，学生就能得出同数学家一样的创造性发现.回忆数学家精彩的发现、巧妙的思想、经典的定理，让师生体验数学的巧妙，深刻地理解知识，感受数学文化的魅力.

新课标注重学生三维目标的培养，在这里，要求学生用自己的方法进行验证，把知识的学习和情感态度与价值观的培养融为一体，无疑有效地培养了学生的科学态度.拼图探究是课程改革所倡导的一种学习方式，利于学生的创新意识和实践能力的培养，把学习的时空还给学生，让学生通过量、折、拼、剪、摆等操作活动理解和掌握三角形内角和定理，同时有效培养学生的发散性思维.

（特约编辑    安   平）