基于数学核心素养的《弧度制（1）》教学设计及反思

高斌

[摘   要]通过现实情境，引入弧度制;将现实情境转化为数学情境，提出问题，寻求弧度制;建立数学模型，确定模型中数学变量，研究变量间的关系;通过检验模型和应用模型，统一角与数的度量单位，实现角的集合与实数集合的一一对应.这些都是提高《弧度制》教学效率的有效措施.

[关键词]数学核心素养;弧度制;教学设计;反思

[中图分类号]    G633.6        [文献标识码]    A        [文章编号]    1674-6058（2019）20-0008-03

一、教材分析

《弧度制》是普通高中课程内容.引入一种新的角的度量方法——弧度制，承接于《任意角的概念》，为扩充后的角度提供了一种更为方便的表示方法，也为后面的三角函数的知识学习打下基础.《弧度制》计划安排两课时，本节课《弧度制（1）》是第一课时.

二、学情分析

1.学生的知识储备是角度制，由于角的概念的推广，学生对角度的范围有了新的认识.现在要引入弧度制，就需要让学生理解为什么要引入弧度制，即学习弧度制的必要性.

2.学生普遍缺乏创造性思维，通过“切圆周角”来定义角度制，可以类似的“切弧长”来定义弧度制，更好地理解弧度制的概念.

3.对于新定义的概念，学生需要结合已学知识，熟练角度制和弧度制的互化，认同弧度制，感受弧度制的优势.

三、教学目标

1.通过情境问题，感受引入弧度制的必要性.

2.类比角度制的定义，经过弧长和半径比值体验探索，理解1弧度的角和弧度的意义.

3.能正确进行弧度与角度的换算，熟记特殊角的弧度数.

4.结合任意角的知识，了解角的集合与实数集R之间建立的一一对应的关系.

5.能正确运用弧度制解决终边相同的角、象限角等有关问题.

四、教学策略分析

本节课的难点在于理解弧度制引入的必要性.教师应该采用探究式教学方法，利用课件设置情境，让学生感受以往角度制六十进制计算的不便，以及角度制解决一些问题的局限性，让学生发现问题、提出问题，迫使新定义一个度量来描述角的大小.利用几何画板和GeoGeobra数学软件，动态展示扇形、圆中弧长与半径的比值和对应圆心角的大小，控制变量，发现两者之间的变化关系，结合生活中常用的十进制，思考并寻求弧度制的可行性，理解1弧度的角和弧度的意义.

五、教学过程

（一）课前准备

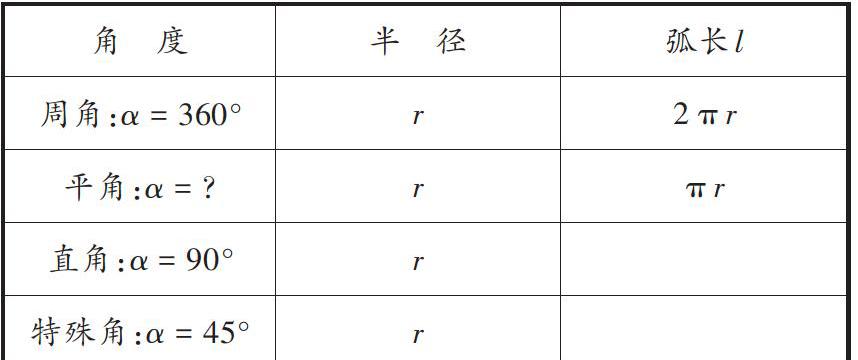
1.已知半径为[r]的圆中，圆心角[α=n°]对应的弧长[l]，根据已学知识完成下表.

2. 角度制的概念，[11°15=]         °，[20°12′36=]         °.

3. 生活中有哪些不同的度量单位？如：长度可以用米、厘米、英尺、码等不同的单位度量.

1米=100厘米=3尺=3.2808399英尺=1.0936133码.

4. 情境：

（1）战场上，迫击炮连在占领阵地后，测得敌人两地堡的间隔是50米，地堡离我方炮连阵地的距离是1000米，为了确保炮兵战士立刻以猛烈的炮火摧毁第一个敌堡后，随即转动迫击炮，摧毁另一个敌堡，如何快速测量或者算出迫击炮对两敌堡的张角（即迫击炮转动的角度）？

（2）射击运动员快速、准确地移动枪支射击移动的目标.运动员根据经验判断离移动目标的距离.那么目标移动的距离如何快速判断？如何计算直接影响运动员移动枪支的角度？

（3）如果想利用导航，则需知晓小船实时所处的经纬度.然而使用量角仪器测量是较为困难的.在已知行驶距离和地球半径的情况下，能度量[θ]的大小吗？

5. 查阅资料，了解六十进制、十进制和圆周率的概念.

【设计意图】熟悉角度制，作为本节课的知识储备，感受角度制六十进制计算的不便.设计情境，体现角度制解决问题的局限性，体现引入弧度制的必要性.

（二）课堂互动

问题1：探究角、半径和弧长之间的关系.

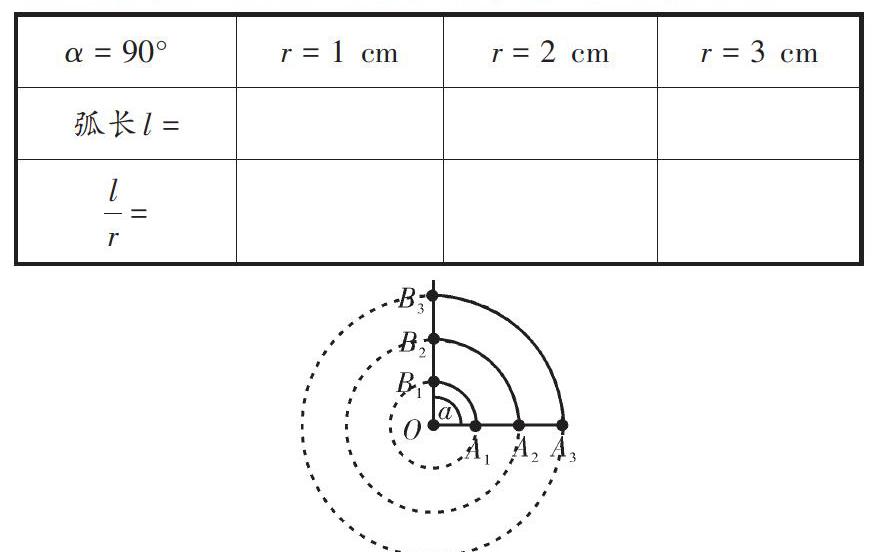
角可以看作平面内射线绕端点旋转形成的图形，取不同长度作为半径，观察相应的弧长变化.

给定一个圆，如果圆心角不变，改变圆的半径，观察弧长的变化趋势，思考：弧长与半径比值如何变化？

结论：角不变时，半径不同，弧长与半径成正比例，并且弧长与半径的比值不变.

特殊[?]一般，是否依然有这样的关系？操作课件演示，答案是肯定的.

问题2：问题1中，如果只改变角的大小，观察弧长和半径的比值如何变化.

结论：此时弧长与半径的比值依然不变，所以对于一个角，角的大小与半径无关.

问题3：当角[α=n°]是定值时，[lr]也是定值，两个定值之间有什么关系？类比角度制中[1°]，是否可以新定义1弧度，如何定义？

结论：角[α]大小与[lr]同步变化且成正比关系，它们一一对应.为了便于计算和度量，选取[l=r]时作为一个单位来度量角的大小，取名“弧度”，此时记为“1弧度”，而[lr]是一個实数，不同于原来的角度制，用[lr]的大小来作为角的弧度数，这样就实现了角的弧度数可以用实数表示，新定义为弧度制.

弧度制概念：长度等于半径长的弧所对的圆心角叫作1弧度（radian）的角，记作1 rad.

用弧度作为角的单位来度量角的单位制称为弧度制.

推广到任意角：按逆时针方向旋转形成的角叫正角，按顺时针方向旋转形成的角叫负角，没有旋转的角叫零角.正角的弧度数是正数，负角的弧度数是负数，零角的弧度数是0.

【设计意图】利用几何画板和GeoGeobra数学软件，动态演示扇形、圆中弧长与半径的比值和对应圆心角的大小，控制变量发现两者之间的变化关系，思考并寻求弧度制的可行性，体现了数学建模的核心素养.

类比角度制“切圆周角”来定义角度制，可以类似的“切弧长”来定义弧度制，体现了数学推理、直观想象和数学抽象的核心素养.

至此可以利用弧度制解决课前准备中的情境问题，根据距离的大小和比值判断角度的大小，体现出弧度制的优越性.

问题4：角度制和弧度制的关系及换算.

常见特殊角的弧度：

问题5：终边相同的角和象限角的弧度制如何表示？

与角[α]终边相同的所有角的集合： ____________; 终边落在y轴的正半轴上：_________________;终边落在x轴上：______________________;第一象限角：___________________________.

【设计意图】 熟练角度制和弧度制的互化，体会弧度制带来的便捷感，体现了数学运算的核心素养.

六、归纳总结

1.  1弧度的意义、弧度制的概念.

2.用弧度制来度量角的大小.

3.角度制和弧度制的换算.

4.弧度制解决问题及其优势.

七、课后作业

1. 完成学案4-102课后作业;

2. 预习学案4-103.

八、教学反思

（一）本节课设计的优点

1. 通过角度制计算的烦琐及角度制解决问题的局限性，引出引入弧度制的必要性.学生通过观察动态课件，思考并寻求弧度制的可行性，发现问题，解决问题，抽象出弧度制的概念，体现了数学抽象的核心素养.

2. 通过“切圆周角”来定义角度制，可以类似的“切弧长”来定义弧度制，展开探究，发挥学生的主观能动性，体现了逻辑推理的核心素养.

3. 角度和弧度之间的换算，弧度制的简单应用，感受弧度制的优越性，体现了数学运算的核心素养.

4.从发现问题到解决问题，从必要性到可行性，从已知到未知，从未知到已知，合理设计每个环节，以“问题串”的形式循序渐进地引导学生.

5. 以“问题串”的形式引发学生合理地思考，充分发挥学生的主观能动性，体现“问题引导、素养优先、学生本位”的课堂教学.

（二）教学中应注意的问题

1.情境问题的引导，如何将问题的困难往距离和距离比值上引导，还需要更多地了解学生的学习基础和思维方式.

2. 为了更好地让学生类比角度制理解1弧度的概念，在对角度和弧度进行互化时，若学生出现将弧度与角度混用的情况，教师应及时地更正并强调书写规范;用弧度制度量角时，如果结果含有[π]，如无特别要求，直接保留[π]的形式，但应明确这里的[π]依然是一个实数.

3. 在動态课件演示过程中，引出弧度制概念时，应与学生多加互动，注意数学语言及提问的技巧，更好地引导学生思考.

（责任编辑   黄桂坚）