向列型液晶流在Lorentz空间中的解的渐近稳定性

林俊宇，邹晨，徐晓杰

（华南理工大学 数学学院，广东 广州 510640）

液晶是区别于气体、液体和固体之外的第四种特殊物质，其中向列型液晶是最常见的类型.本文将研究下面不可压向列型液晶流的柯西问题：

和初值条件

文献[1]在Koch-Tataru[2]框架下，得到了小初始值问题的温和解的存在性.文献[3]研究了文献[1]的温和解的正则性(也可见文献[4]).林和丁在Lebesgue空间的框架下，得到了小初值问题的解的存在性[5].在Lorentz空间的框架下，文献[6]得到小初值的整体温和解的存在性.文献[7]研究了温和解的唯一性.对于Besov空间中的温和解，可参见文献[8-10].对于弱解以及强解的研究，参见文献[11-15].对于不可压液晶流的其他研究成果，参见文献[16].

本文将研究在弱-Ln空间（记为L(n，∞)(ℝn)）中温和解的渐进稳定性.首先回顾Lorentz空间的有关记号和性质.

设f为可测函数，p，q为正实数.定义

引理1[18-19]（广义Young不等式）记T为卷积算子以及h=T(f，g)为f与g的卷积.

引理2[18]（广义Hölder不等式）设满足如果和g∈那么其中s≥1是满足的任意常数.并且有估计其中

下面给出一些函数空间记号.

给定常数q＞n，记是满足下面条件的所有实值函数的集合：

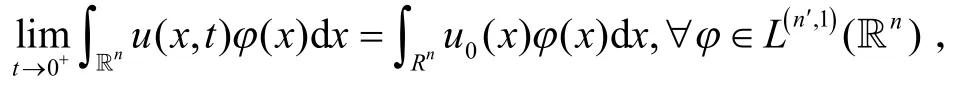
记ℙ为L2(ℝn)上到的正交投影算子.Stokes算子-ℙΔ和Laplace算子-Δ在Lorentz空间中分别生成一致有界解析半群

方程组（1～4）可重写为下面的积分形式

其中（记*为函数的卷积运算）

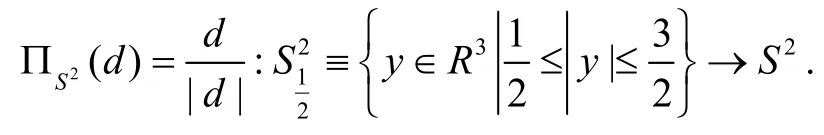
引理3[6]99设f，g∈X，那么，对q＞n有

并且有估计

引理4[6]99设q＞n.假设那么

特别地，当h≡1，有

引理5[21]对于t＞0，设是两个正函数.如果存在正函数1(0，1)f∈L满足并且

那么存在另外一个正函数1(0，1)g∈L使得

下面是由文献[6]得到的存在性结果.

定理1[6]101设满足∇⋅u0=0和d0∈S2，∇d0∈L(n，∞)(ℝn).那么存在常数ε0＞0使得当时，方程组（1～4）有整体温和解(u，d)满足

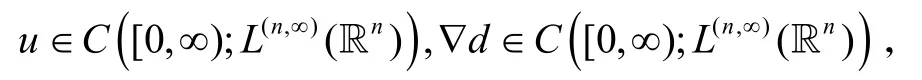
且对q＞n，

本文的主要结果是

定理2给定q＞n.设u0，v0∈L(n，∞)(ℝn)满足∇⋅u0=∇⋅v0=0以及d0，h0∈S2满足∇d0，∇h0∈L(n，∞)(ℝn).设由定理1得到的（1～4）对应初始值的解分别为(u，d)和(v，h).假设

那么

若进一步假设

那么

证明我们只需证明在式（9）和（11）的条件下式（12）是成立的，因为式（10）可以用类似的方法证明.先估计

事实上，对于t＞0，

由引理3可得

以及

类似地，可得

因此

其中C(n，q)是正常数，仅依赖于

事实上，对t＞0，

类似引理4的证明，可得对t＞0，

结合式（13～14），可得

记A(t)=A1(t)+A2(t)，其中

以及

利用变量替换τ=st，其中s∈[0，1]，由式（15）可得

定理2证毕.