基于缸压信号的星型压缩机动力学分析

楼京俊，李超博，张振海，宁荣辉

1海军工程大学舰船与海洋学院，湖北武汉 430033

2海军工程大学动力工程学院，湖北武汉 430033

0 引 言

往复式压缩机以排气压力高、输出压力覆盖范围广、制造精度要求相对较低等优势被广泛应用于石油、化工、冶金及船舶等行业［1］。作为船舶气动系统的“心脏”，其生产的压缩空气主要用于启动柴油机与倒车、加强海损邻舱、吹除各类管阀等。特种船舶大多是采用多级串联的往复式压缩机，其机型种类多样［2］。星型往复式压缩机因具有结构紧凑、动力学设计合理、振动相对较低等优势逐渐得到应用［3］。虽然国内已有相关机型投入生产，但相关理论研究还处于起步阶段。

星型压缩机运动部件是采用曲柄连杆机构将机械能转化为气体压力能，为内燃机工作的逆过程，但其气缸布置要求低于内燃机要求。该型压缩机正是利用气缸布置的优势，在保证输出压力的同时能有效平衡自身的二阶惯性力，从而可以在一定程度上减小压缩机振动［4］。由于压缩机气缸内为高温、高压环境（最高压力可达20 MPa以上，而一般的内燃机最高压力不会超过10 MPa），因而对传感器和密封条件要求较高，只有这样才能有效测取气缸压力。

在国内，对往复式压缩机的研究多集中于曲轴动力学特性［5］、动平衡［6］、运动副间隙［7］等方向。在压缩机运转过程中，主轴承承受的载荷呈周期性变化，故而会产生曲轴弯曲及扭转振动，从而直接影响整机的安全性和稳定性，这种现象在多列、高速压缩机中更为明显［8］。动平衡则是研究曲柄连杆机构的常见问题，最基础是采用平衡重来消除部分惯性力，也有采用平衡轴的方法，若要完全平衡二阶惯性力，则需采用双轴平衡法［9］。然而，由于平衡轴成本较高、结构复杂、占用空间大，通常情况还是采用平衡重的方法。运动副间隙是近几年研究的热点［10］，主要研究的是运动副材料、轴向尺寸、建模方式、间隙大小、碰撞及摩擦对其动力学特性的影响，但相关研究仍在理论阶段［11-14］。

本文将采用HTT-04CA型缸压传感器，采取阀杆钻孔的方法，测取不同工况下气缸压力随曲柄转角变化的曲线。通过理论推导和建立ADAMS动力学模型，分析主轴承所受惯性力和平衡重质量对主轴承受力的影响。结合实测的缸压信号，将其周期延拓，构造一定时域长度的SPLINE曲线，将其加载到ADAMS动力学模型的各个活塞质心。仿真分析主轴承的受力情况，通过分析缸盖和底座的振动测试数据，对整机部分测点的振动情况进行研究。

1 空压机结构形式

该型压缩机为单作用立式星型结构，采用水冷、四级压缩，各级气缸以立式曲轴为中心，呈90°星型放射状向四周分布，各级连杆并排布置在同一个曲柄销上，以缩短曲轴长度、提高曲轴固有频率，从而使整机更为紧凑。其中一、二级与三、四级气缸分别对称布置，一、二级连杆位于曲柄两端，最大程度地平衡自身惯性力。机身通过曲轴箱支架安装在底座上，曲柄连杆机构及气缸分布如图1所示。压缩机工作时，电机通过弹性联轴节带动曲轴旋转，连杆驱动活塞做往复运动。空气经进气消音器过滤后进入一级气缸，压缩气体再经冷却器冷却，进入油水分离器，然后逐次进入下一级气缸进行压缩、冷却、分离，完成四级气缸压缩后，由末级出口排出。各级气缸依次完成吸气—压缩—排气—膨胀4个工作过程。

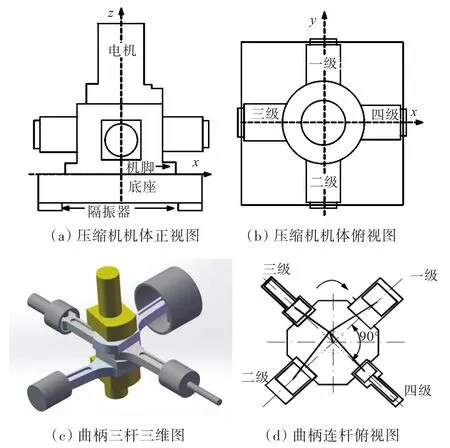
图1 曲柄连杆机构及气缸分布示意图Fig.1 Schematic diagrams for the distribution of the crank connecting rod mechanism and cylinder

2 曲柄连杆机构

2.1 惯性力和力矩

曲柄连杆机构直角坐标示意图如图2所示（图中φ3为相邻两级气缸中心线的夹角），则一阶往复惯性力为：

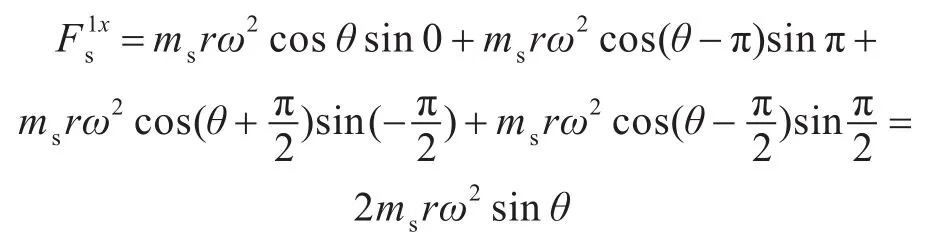
式中：ms为往复质量；r为曲柄半径；ω为曲柄旋转角速度；θ为曲柄转角。

图2 曲柄连杆机构直角坐标示意图Fig.2 Cartesian coordinates of the crank connecting rod mechanism

将主轴承所受曲柄连杆机构惯性力按泰勒级数展开，指数n即为惯性力的阶次，一般情况下只考虑前两阶惯性力。y轴与一阶往复惯性力的夹角 θ1为

理论上可增加平衡质量，使一阶惯性力和力矩平衡。同理，可计算得到二阶往复惯性力和力矩为：

式中：λ为曲柄连杆的长度比；a为相邻两列连杆的轴向距离。由于各列之间的间距a相对较小，因而二阶惯性力矩也较小，在平衡往复惯性力时主要考虑一阶往复惯性力。

2.2 ADAMS动力学模型

该型压缩机曲柄连杆机构共有113个零部件，通过CATIA进行布尔操作，将其合成为4活塞、4连杆和1曲轴共9个零部件，并去除模型的油孔、倒角等细节部分。由于CATIA与ADAMS的数据交换不是很方便，故将CATIA模型保存为stp格式文件后，导入PROE另存为*.x_t格式文件，从而得到Parasolid实体，将实体导入ADAMS/View中，定义质量属性。不同部件之间用移动副和转动副相连接，平衡铁与曲轴固定，添加曲轴驱动，转速为1 480 r/min，得到动力学模型如图3所示［15-16］。其中，活塞质量均定义为5 kg，曲轴和连杆是基于steel材料属性而得到，曲轴质量为33 kg，一、二级连杆质量为3.96 kg，三、四级连杆质量为3.98 kg。

图3 曲柄连杆机构ADAMS动力学模型Fig.3 ADAMS dynamic model of the crank connecting rod mechanism

各部件定义为刚体，平衡铁的形状和位置相对曲轴保持不变。考虑星型布置的对称性，以主轴承x方向受力最小为优化目标，得到平衡重质量随主轴承 x方向受力的变化曲线如图4（a）所示。随着平衡重质量m的增加，主轴承x方向的受力Fx先减小后增大，理论上最佳质量为5.65 kg，能使主轴承x方向受力最小。在平衡重取得最佳质量的情况下，曲轴旋转副受力频域图如图4（b）所示。由于三、四级连杆质量比一、二级连杆重0.02 kg，因而二阶惯性力没有完全平衡，但比一阶和三阶的都小。

图4 空载主轴承受力图Fig.4 Force diagram of the main bearing in unloaded state

3 气缸压力测试

3.1 测试方案

本次压缩机气缸压力测试主要设备有：气缸压力传感器、24 V直流电源、NI数据采集卡和笔记本电脑。由于传感器和采集卡接口问题，还需要配备通道连接BNC接头和500 Ω精密电阻。为了避免在气缸压力采集过程中出现通道效应，将压力传感器布置在正对活塞的顶部，从气阀阀杆中打孔，将高压气体引出后再进行测量。传感器布置如图5所示，从5 MPa开始，每隔5 MPa为1个工况，一直测到25 MPa，共5个工况。由于只有2个气缸压力传感器，所以每次数据采集时只能两缸同时进行，然后停机进行调换。4个气缸压力之间相互衔接，通过重叠其中一个缸的缸压来确定4个气缸压力的实时对应关系。

图5 气缸压力传感器布置Fig.5 Arrangement of cylinder pressure sensor

3.2 测试数据分析

空压机整机激励力主要包括气体力、摩擦力、气阀撞击力、活塞侧推力和主轴承激励力，其中气体力占主导作用。虽然可以通过相关公式进行计算，但计算的可靠性有待验证。通过压力传感器对气缸压力进行采集，可得到可靠的气缸压力值。各工况下的气缸压力情况如图6所示。理论上，压缩机的吸气压力和排气压力保持不变，但实际情况并非如此，吸、排气压力与气阀的性能有很大关系。

图6 各工况下的气缸压力变化曲线Fig.6 Variation curves of cylinder pressure under different working conditions

在整个测试过程中，一级气缸的气缸压力变化不大，二级气缸的最大气缸压力也处于1.4～1.6 MPa。可见，最终排气压力的变化对一、二级气缸的影响不大，一级气缸在25 MPa工况下最大负压可达0.16 MPa；在排气阶段，三、四级气缸的气缸压力会有明显波动，主要原因是排气压力较高，引起了气阀的颤振，其中三级气缸的最大气缸压力变化范围为5.7～9.2 MPa，四级气缸则随最终排气压力出现了大幅波动。在5 MPa工况下，四级气缸对提高气体压力没有起到作用，而在25 MPa工况下，四级气缸的气缸压力从6.8 MPa升至25 MPa。

4 动力学分析

4.1 曲柄连杆机构动力学分析

在25 MPa工况下，当气缸压力通过气缸截面积转化为活塞所受气体力时，得到活塞所受气体力随曲柄转角的变化规律如图7所示。将活塞所受气体力进行周期延拓，构造SPLINE曲线，并加载到ADAMS模型上。主轴承受力F的时域曲线如图8所示。曲柄连杆机构旋转一周耗时0.405 s，在一个周期内，主轴承受力有2次明显的峰值，这相对于一般的一至四级气缸压缩减少了2次受力波动。将图8的时域信号转化到频域，得到主轴承频域受力曲线如图9所示。由于信号中存在甚低频成分，会引起低频信号畸变，因此没必要关注频域第一个波谷以前的力信号［17］。主轴承主要承受一阶惯性力，其次是三阶。由于活塞所受气体力不平衡，故二阶惯性力有一定的攀升，但依然低于三阶惯性力，因此该结构对二阶惯性力仍有一定的抑制作用。

图7 活塞所受气体力随曲柄转角变化曲线Fig.7 Variation curves of the gas force on the piston with the crank angle

图8 主轴承受力时域图Fig.8 Time domain diagram of the main bearing force

图9 主轴承受力频域图Fig.9 Frequency domain diagram of the main bearing force

4.2 振动信号分析

沿各级活塞的运动方向，在相应的气缸盖上布置传感器，测试得到缸盖振动信号时域曲线如图10所示。由图可见，一级气缸的振动剧烈程度明显高于其他三级气缸。主要原因是一级气缸的缸径较大，引起局部结构刚性不足，并且一级气缸在吸气的过程中存在较大负压，受力情况相对复杂，加上吸气引起消声器振动，使得一级气缸的振动加剧。缸盖振动信号频域曲线如图11所示。由图可见，一级气缸的振动主要集中在高频段，在低频段振动并不突出。

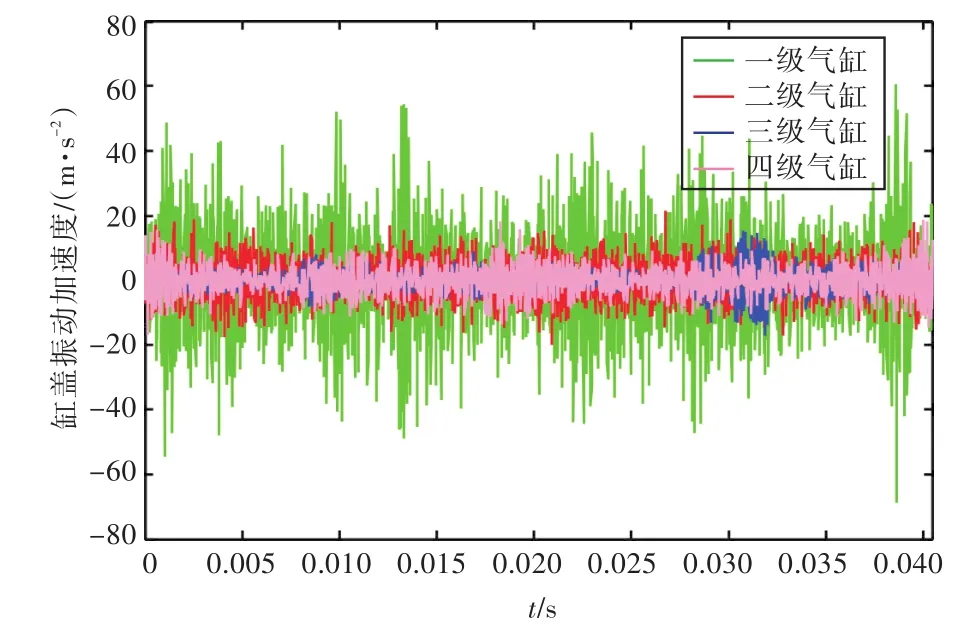
图10 缸盖振动信号时域图Fig.10 Time domain diagram of the cylinder head vibration signal

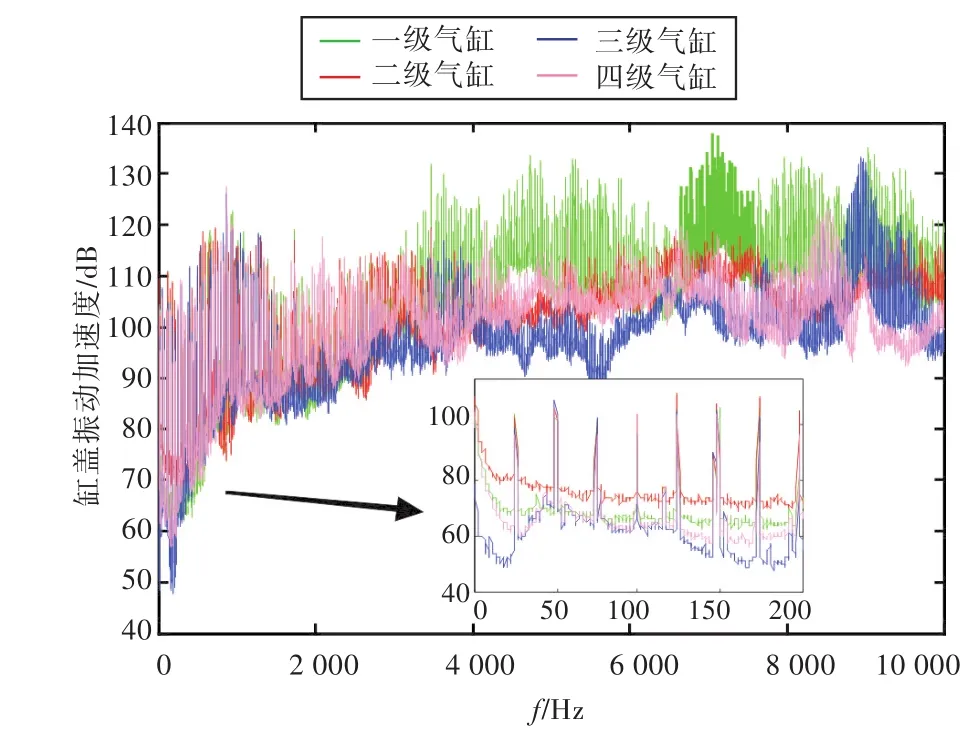
图11 缸盖振动信号频域图Fig.11 Frequency domain diagram of the cylinder head vibration signal

总振级 L的计算公式为［18］

式中：ai为频域加速度，m/s2；b为加速度的带宽，m/s2；a0=10-6，为参考加速度，m/s2。

1～4号机脚测点的总振级如表1所示。为便于对比柱状图与总振级的变化规律，将所有点的加速度振级减去129 dB（若不减去129 dB，柱状图用肉眼看不出差别），得到参考加速度级与压缩机工况的关系如图12所示。同种工况下，底座4个测点振动加速度级之间最大相差4.1 dB，说明压缩机重心相对于底座中心线有所偏移。对比整体趋势，工况变化对底座振动加速度级的影响不超过1.8 dB，在低于10 MPa的工况下（包括10 MPa）和高于10 MPa的工况下振动有所不同。

表1 不同工况下机脚4个测点的总振级Tab.1 Total vibration level of each point under different working conditions

图12 各工况下机脚参考加速度级Fig.12 Acceleration level of each point under different working conditions

5 结 论

本文以星型压缩机为研究对象，通过试验对气缸压力和振动加速度进行测试，结合建立的曲柄连杆机构ADAMS模型对星型压缩机展开动力学分析，得到如下结论：

1）从理论上看，该型压缩机气缸布置能有效平衡二阶惯性力。由于连杆质量的分布存在偏差，二阶惯性力会有所增加，但仍然小于三阶惯性力。

2）一级气缸在压缩机的运行过程中存在较大负压，振动相对于其他缸更加剧烈；压缩机工况变化对一、二级气缸的气缸压力影响不大，主要影响三、四级气缸的气缸压力。

3）在低压工况下，4个气缸对提升排气压力没有太大作用，反而会加剧底座的振动，因而该型压缩机不适合在低于10 MPa的工况下工作。压缩机工况变化对底座振动加速度级的影响不超过1.8 dB，在15 MPa及以上工况底座的振动加速度级相对平稳。

4）本文直接认为缸压的测试结果在误差范围内是可信的，后期可研究测压通道长度和直径对测试结果的影响，这需要进一步分析振动机理，并将振动测试结果与有限元仿真结果进行对比。