内嵌声学黑洞薄板振动特性数值模拟方法研究
2019-08-23王博涵杨德庆夏利福
王博涵 ,杨德庆*,夏利福
1高新船舶与深海开发装备协同创新中心,上海200240
2上海交通大学海洋工程国家重点实验室,上海200240
3上海交通大学船舶海洋与建筑工程学院,上海200240
0 引 言
声学黑洞(Acoustic Black Hole,ABH)效应是指在通过合理控制面板厚度且遵循幂函数变化逐渐减小为零的过程中,面板内弯曲波传播速度逐渐减小,在理想情况下,当面板厚度为0时,波速衰减为0而波幅趋于无穷的现象。声学黑洞的概念及基本理论由 Pekeris[1]在 1946 年提出,他发现在靠近海岸线处海水深度逐渐减少,海水中声波的相速度也会随之逐渐衰减为0,因此不发生反射。随后,Mirnov[2]在楔形结构中发现固体结构内部的弯曲波存在类似的现象。Krylov等[3-6]将声学黑洞概念应用于梁、板壳结构的减振中,并在理论、数值与实验3个层面对梁、平板内的声学黑洞效应进行了系统性研究。现有研究表明,声学黑洞区域的厚度变化若遵循幂函数衰减规律,且幂函数的指数不小于2,则弯曲波传播至声学黑洞区域时,由于结构厚度减少,波速会逐渐减小,波长变短。当声学黑洞区域接近厚度为0的位置时,累计相位趋于无穷大,弯曲波被永远局限在声学黑洞区域内。声学黑洞结构通过控制厚度变化来达到聚集结构弯曲波的效果,在船舶、航天器和车辆等结构的振动能量控制、结构减振降噪等方面有潜在应用价值。
目前,在声学黑洞研究中,数值仿真方法的应用最为广泛。黄薇等[7]使用有限元软件建立二维声学黑洞模型,研究弯曲波在声学黑洞区域的时域传播过程,结合有限元数值结果与振动功率流的结果,分析弯曲波能量聚集过程。Conlon等[8]将多个二维声学黑洞结构以周期性规律布置在薄板结构中,结合均匀板的响应特征,计算并综合分析该薄板结构的振动和声辐射特性。Jia等[9]将二维声学黑洞板与动力吸振器相结合,在板的声学黑洞区域连接一个弹簧质量系统,分析整个板的振动响应特征。上述数值仿真模型均采用体单元进行离散。
对于二维声学黑洞板,其厚度远小于长、宽方向的尺度。在使用体单元进行离散时,为保证单元在3个方向的尺度相差不是太大,需要在结构的长、宽方向上划分大量单元。因此,使用体单元进行数值模拟存在单元数量多、计算效率低的缺点。而二维声学黑洞区域板厚度与另外2个方向的尺度相比属于薄板的范畴,从力学特性角度分析,合理选择划分网格的尺度,使用板壳单元离散得到的计算结果也应是可靠的。
因此,本文拟对内嵌二维声学黑洞薄板采用板壳单元模拟声学黑洞效应的方法进行深入研究,并与体单元离散建模的计算结果进行对比,验证使用板壳单元模拟声学黑洞效应的可靠性。最后讨论声学黑洞区域厚度阶梯变化尺度以及幂律对其振动性能的影响。
1 声学黑洞基本理论
二维声学黑洞结构示意图如图1所示,其中声学黑洞区域的半径由rABH表示。二维声学黑洞区域xOz截面的厚度遵循幂函数式:

式中:h(x)为距中心点x处声学黑洞结构(板)的厚度;ε为常数;幂律m为正有理数,被称为黑洞效应指数因子。Mironov[2]已证明,当结构的厚度变化满足幂函数曲线且指数不小于2时,就能满足结构声学黑洞的基本要求,将传导至声学黑洞区域的弯曲波全吸收。

图1 二维声学黑洞结构示意图Fig.1 The structure of two-dimensional acoustic black hole
弯曲波在二维声学黑洞结构中传播的控制方程为[10]


式中:A(x,y)为振幅;φ(x,y)为相位;kp为波数。将式(3)代入式(2),若使等式成立,则等式右侧的实部和虚部必须为0。由实部等于0并舍弃关于 A(x,y)和 φ(x,y)的高阶导数项,即可得到
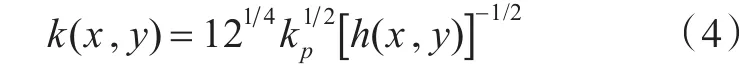
式中,k(x,y)为与位置有关的波数。
二维声学黑洞是由一维声学黑洞的截面h(x)=εxm(m≥2)以 x=0点为中心旋转1周形成的,因此,一维声学黑洞的特性可以一定程度上反映二维的情况。对于xOz截面,式(4)可写为

根据式(5),当 x→0时,弯曲波波数将趋于正无穷,这意味着弯曲波波速将趋于0,波幅则趋于无限大,振动将被局限在声学黑洞中心区域。因此,理想的声学黑洞在理论上可以100%吸收板内弯曲波,取得显著的减振降噪效果。
在实际加工制造过程中,板厚无法严格遵循幂函数连续变化至0,总会在接近黑洞区域中心存在一个截断厚度。当板厚小于截断厚度时不再继续衰减,而是维持在常量h0。这导致声学黑洞区域无法“吞噬”全部弯曲波,而会对入射波产生一定反射。虽然截断厚度不可避免,但如果将阻尼材料附加于声学黑洞区域,就能有效降低黑洞区域的弯曲波反射率[11]。
2 结构模型
基于文献[7]中的二维声学黑洞板算例,设计了3种四边简支矩形板模型。
模型1:四边简支均匀厚度矩形薄板,板长a=600 mm,宽 b=400 mm,板厚 h=5 mm,如图 2所示。板的材料为钢,密度为7 850 kg/m3,弹性模量为210 GPa,泊松比为0.3,结构阻尼系数为0.02。

图2 四边简支均匀厚度矩形薄板Fig.2 The simply supported rectangular uniform thin plate
模型2:在模型1基础上,板心处开出半径r=100 mm的圆孔,如图3所示。

图3 中心处开孔的均匀厚度矩形薄板Fig.3 The rectangular uniform thin plate with a hole in the center
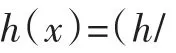

图4 中心处变厚度的二维声学黑洞板Fig.4 The two-dimensional ABH plate with variable thickness in the center
在点(-260 mm,0,0)处施加1 N的正弦激励力,激励频率为 1~8 000 Hz,频率步长为 10 Hz。选取图2~图4中所示的4个振级评价点,输出各点的振动速度级并进行对比。其中振动速度级的参考值为10-9m/s。评价点1~4的坐标分别为(160 mm,0,0)、(230 mm,0,0)、(154.445 mm,102.014 mm,0)和(230 mm,160 mm,0)。
3 内嵌二维声学黑洞薄板振动特性的数值模拟
3.1 基于体单元建模方法的声学黑洞效应数值模拟
采用体单元对图4所示的声学黑洞板(模型3)进行离散,得到如图5所示的有限元模型。该模型共有86 000个单元,108 105个节点。网格划分时,黑洞区域体单元长度为2 mm,沿板厚度方向划分4层体单元。四边简支边界条件施加在板厚度方向的中间面块体节点处。在激励点一侧选取评价点5,坐标为(-230 mm,0,0),比较载荷作用端同侧的评价点5与黑洞另一侧评价点1~4的振动速度级,以此判断声学黑洞是否能吸收弯曲波,进而减小振动响应。

图5 体单元离散的二维声学黑洞板有限元模型Fig.5 The finite element model of two-dimensional ABH plate with solid elements
使用MSC/Patran有限元软件对声学黑洞板进行频响分析,激励力频率范围为1~8 000 Hz,频率步长为10 Hz,计算5个评价点的振动速度级,结果如图6所示。
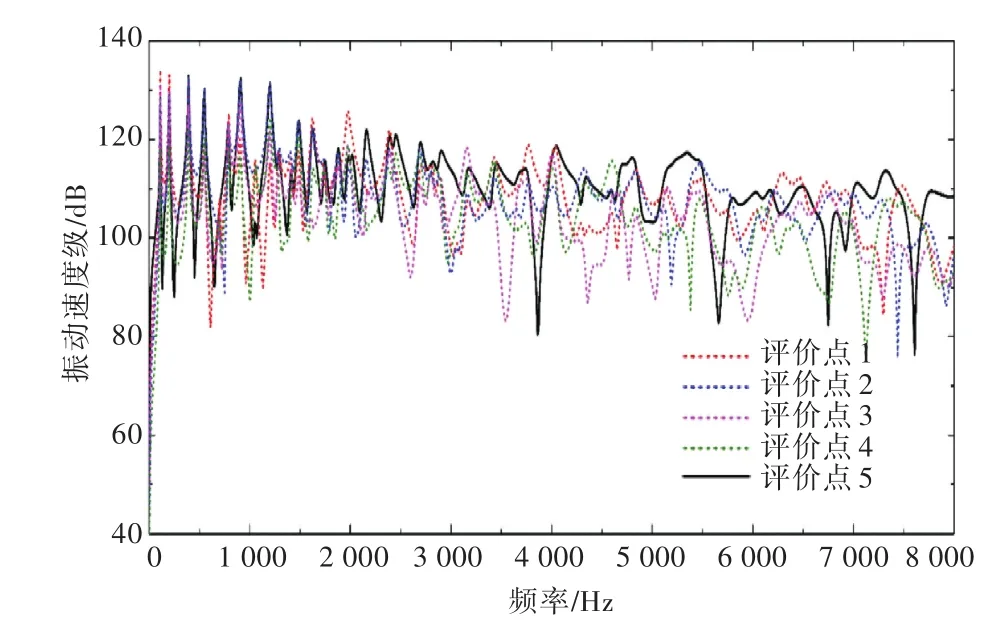
图6 5个评价点振动速度级对比结果Fig.6 Comparison of vibration speed level between five evaluation points
由图6可见,5个评价点的振动速度级在低频段相差不大,这说明低频时声学黑洞效应并不明显。在大部分高频段,评价点1~4的振速小于评价点5的振速,这说明弯曲波在经过黑洞后,由于结构的声学黑洞效应,导致板右侧的振动减小。算例中的声学黑洞不是理想黑洞,在黑洞中心处存在截断(中心等厚度区域),不可能吸收所有的弯曲波,但是根据Krylov等[11]的研究,在黑洞中心截断区域表面敷设少量阻尼会有很好的吸收效果。
3.2 基于板壳单元建模方法的黑洞效应数值模拟
根据弹性力学和有限元法关于板壳力学的特性理论,在计算效率和计算精度2个方面,采用板壳单元离散声学黑洞板计算应该优于等量单元数情况下采用体单元离散板结构后的相关计算。本文采用板壳单元离散声学黑洞板,并讨论其与采用体单元离散声学黑洞板的计算结果的等效性。首先介绍有限元模型的网格划分方式,然后对结构模态以及在1~8 000 Hz单位激励下板的频率响应进行对比。
3.2.1 有限元模型
对4种有限元模型进行讨论:
1)有限元模型(a),采用板壳单元模拟模型1所示的均匀厚度薄板(共有21 500个单元、21 621个节点);
2)有限元模型(b),采用板壳单元模拟模型2所示中心处开孔的均匀厚度薄板(共有6 000个单元、6 220个节点);
3)有限元模型(c),采用板壳单元(单元长度为2 mm)模拟模型3所示声学黑洞板(共有21 500个单元、21 621个节点);
4)有限元模型(d),采用体单元(单元长度为2 mm)模拟模型3所示声学黑洞板(共有86 000个单元、108 105个节点)。
有限元模型(a)和(c)如图7所示,两者的区别仅在于板厚度参数的设置不同。对于有限元模型(c),黑洞区域有限元模型被离散成阶梯厚度板,单元宽度为2 mm,厚度依照幂律变化。有限元模型(b)如图8所示。有限元模型(d)如图5所示。

图7 有限元模型(a)和(c)Fig.7 Finite element model(a)and(c)

图8 有限元模型(b)Fig.8 Finite element model(b)
3.2.2 模态分析
根据四边简支矩形薄板固有频率的解析解公式,均匀厚度薄板前5阶固有频率为
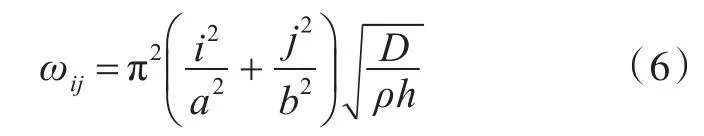
式中:i和j分别为薄板在长度和宽度方向上的半波数。
使用MSC/Patran有限元软件对上述4种模型结构进行模态计算,其前5阶固有频率如表1所示。板壳单元离散的声学黑洞板的前5阶振型图如图9所示,体单元离散的声学黑洞板的前5阶振型图如图10所示。
由表1可见,薄板前5阶固有频率的解析解和数值解相吻合,误差小于1%;此外,声学黑洞板的固有频率介于薄板与开孔板两者之间或与两者接近。

表1 4种模型的前5阶固有频率Table 1 First five order natural frequencies of four models


图9 板壳单元离散的声学黑洞板前5阶振型图Fig.9 The first five modes of ABH plate with shell elements

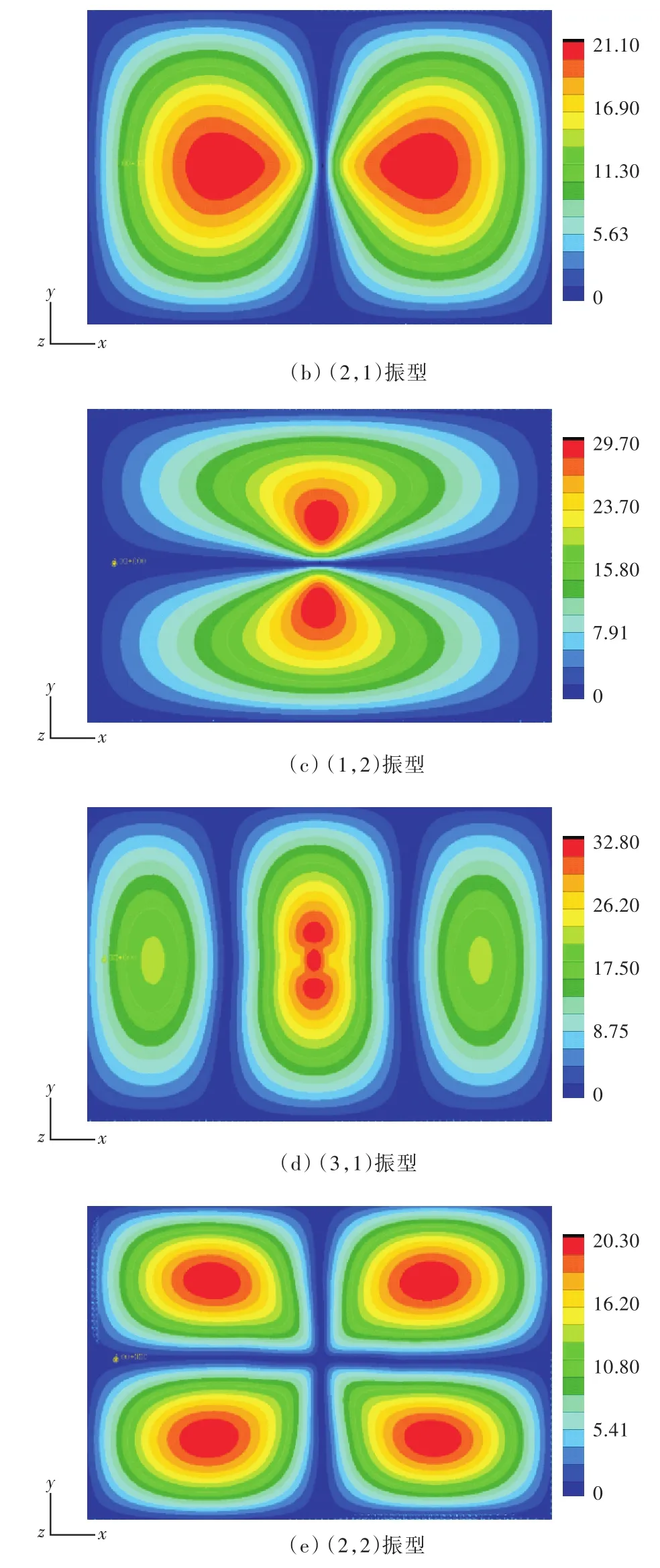
图10 体单元离散的声学黑洞板前5阶振型图Fig.10 The first five modes of ABH plate with solid elements
对比使用板壳单元和体单元模拟声学黑洞板的固有频率计算结果,可以看到,两者非常接近,板壳单元离散声学黑洞板的固有频率计算结果普遍小于同阶次体单元离散的计算结果,相对误差为5%~9%。由图9和图10可以看出,2种模拟方法的前5阶振型图基本相同。至于(3,1)阶振型的情况,本文关注的是结构的整体模态,体单元建模振型图的中心区域与板壳单元的不同,是因为此时钢板的整体模态图形显示受到了局部模态图形显示比例尺度的影响。总之,计算结果验证了板壳单元建模在模态计算方面的合理性,且计算误差较小。
3.2.3 频率响应分析
施加前文所述激励力进行频响分析,激励力频率范围为1~8 000 Hz,频率步长为10 Hz。对有限元模型(a),(c)和(d)进行频响计算,计算结果如图11所示。
由图11可见,采用板壳单元和体单元模拟声学黑洞板,在低频段,板壳单元和体单元离散的2种模型评价点的计算结果较吻合;在高频段,因固有频率存在一定差异,两者响应计算结果的峰值位置有一定差异,但峰值十分接近。这说明采用板壳单元模拟声学黑洞板的计算结果也是精确可靠的。

图11还反映了声学黑洞板的减振性能。采用两种方式建模的声学黑洞板与薄板(模型(a))相比,三者在低频段的振动速度级基本吻合,这说明声学黑洞板在低频段减振效果不明显。对于高频段,可以看到声学黑洞板的减振效果很明显,与文献[10]的研究结果相同,说明采用板壳单元模拟声学黑洞板时,其频响计算结果也体现了黑洞效应。
4 黑洞区域厚度阶梯变化尺度对声学黑洞板振动性能的影响
4.1 黑洞区域厚度阶梯变化尺度对模态特性的影响
对黑洞区域离散时,板厚度阶梯变化尺度分别取5,10和16 mm进行建模,分析黑洞区域厚度阶梯变化尺度对声学黑洞板振动性能的影响。
声学黑洞区域板厚分布不均匀,满足幂律变化规律,厚度在板中心处逐步变薄。因此,模态分析时在黑洞区域会出现局部模态,在某些特定频率,黑洞中心区域会发生共振,吸收能量。图12给出了厚度阶梯变化尺度为2 mm时黑洞区域的一阶局部模态。
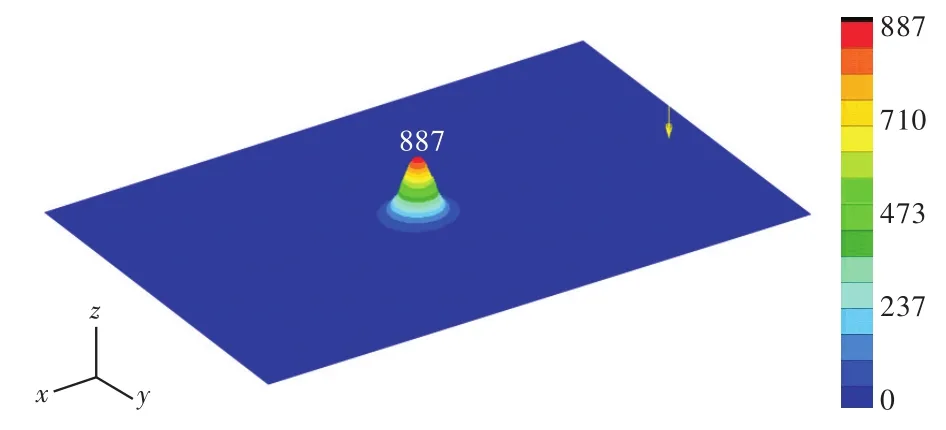
图12 厚度阶梯变化尺度为2 mm时黑洞区域一阶局部模态振型Fig.12 The first order local mode with 2 mm step change scale
研究发现,厚度阶梯变化尺度的改变会导致黑洞区域局部共振频率发生变化。厚度阶梯变化尺度分别为2,5,10和16 mm的一阶局部模态对应的固有频率如表2所示。

表2 不同厚度阶梯变化尺度一阶局部模态对应的固有频率Table 2 Natural frequencies of first order local mode with different step change scales
由表2可见,厚度阶梯变化尺度对局部模态对应的固有频率产生较大影响,且随着厚度阶梯变化尺度的增大,局部模态对应的固有频率会大幅降低。在实际应用中,局部模态可以起到吸收振动能量的作用,因此合理调整厚度阶梯变化尺度,可以将声学黑洞板的局部模态对应的固有频率调整到预期减振频率。
4.2 黑洞区域厚度阶梯变化尺度对频率响应的影响
施加前文所述激励力,对黑洞区域厚度阶梯变化尺度分别为2,5,10和16 mm的声学黑洞板进行频响分析,计算结果如图13所示。

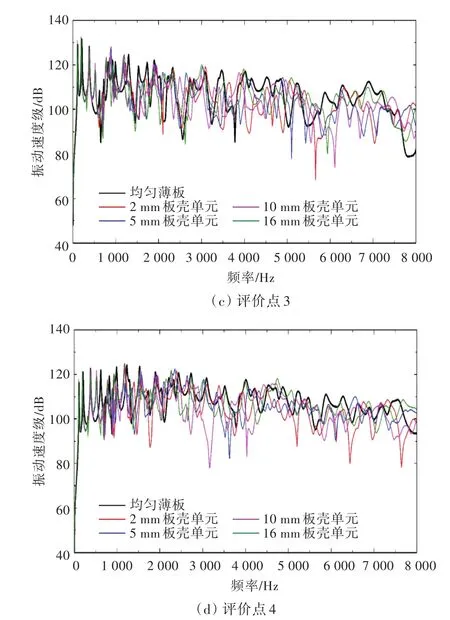
图13 不同厚度阶梯变化尺度情况下4个评价点的振动速度级Fig.13 Vibration velocity level of four evaluation points in the case of different step change scales
分析图13可知,低频时不同厚度阶梯变化尺度声学黑洞板的速度响应吻合较好,与无声学黑洞薄板振速相比,没有明显的减振效果。高频时不同厚度阶梯变化尺度的声学黑洞板均具有声学黑洞效应,有明显的减振效果,且其减振频率范围不同。由此说明,合理调整厚度阶梯变化尺度可以对目标频段进行减振设计。
5 幂律变化对声学黑洞板振动性能的影响
5.1 幂律变化对声学黑洞板模态特性的影响
在幂律m=3,4的情况下,黑洞区域厚度阶梯变化尺度取2 mm,对板壳单元和体单元离散声学黑洞板进行模态分析,并与m=2声学黑洞板的计算结果进行比较。幂律变化对声学黑洞板整体模态特性的影响如表3所示。
由表3可以看出,幂律变化对声学黑洞板整体固有频率的影响很小,无论采用板壳单元还是体单元离散声学黑洞板,固有频率的计算结果基本一致。在幂律相同的情况下,使用体单元离散的声学黑洞板的整体固有频率要高于板壳单元离散的情况。
幂律变化对黑洞区域局部模态特性的影响如表4所示。其中,m=2时,板壳单元离散模型的前3阶局部模态振型如图14所示,对于m=3,4的情况,其前3阶局部模态振型与m=2的情况类似,在此不再赘述,仅列出具体的固有频率值。
以上计算结果表明,当幂律越大时,由于声学黑洞板黑洞区域厚度变化较为剧烈,黑洞中心区域的板厚相比邻近区域更薄,导致黑洞区域的局部共振模态在频率很低的情况下就会出现。由表4可见,m=4时,一阶局部模态在37.04 Hz出现;m=3时,一阶局部模态在168.69 Hz出现。对于高幂律的情况,与m=2相比,低频的局部模态十分密集。模态计算结果还表明,采用板壳单元和体单元模拟局部模态的结果存在一定差异,板壳单元模拟的局部模态结果要低于体单元模拟的情况。

表3 幂律变化对声学黑洞板前5阶整体固有频率的影响Table 3 Influence of power law variation on the first five order natural frequencies of ABH plate
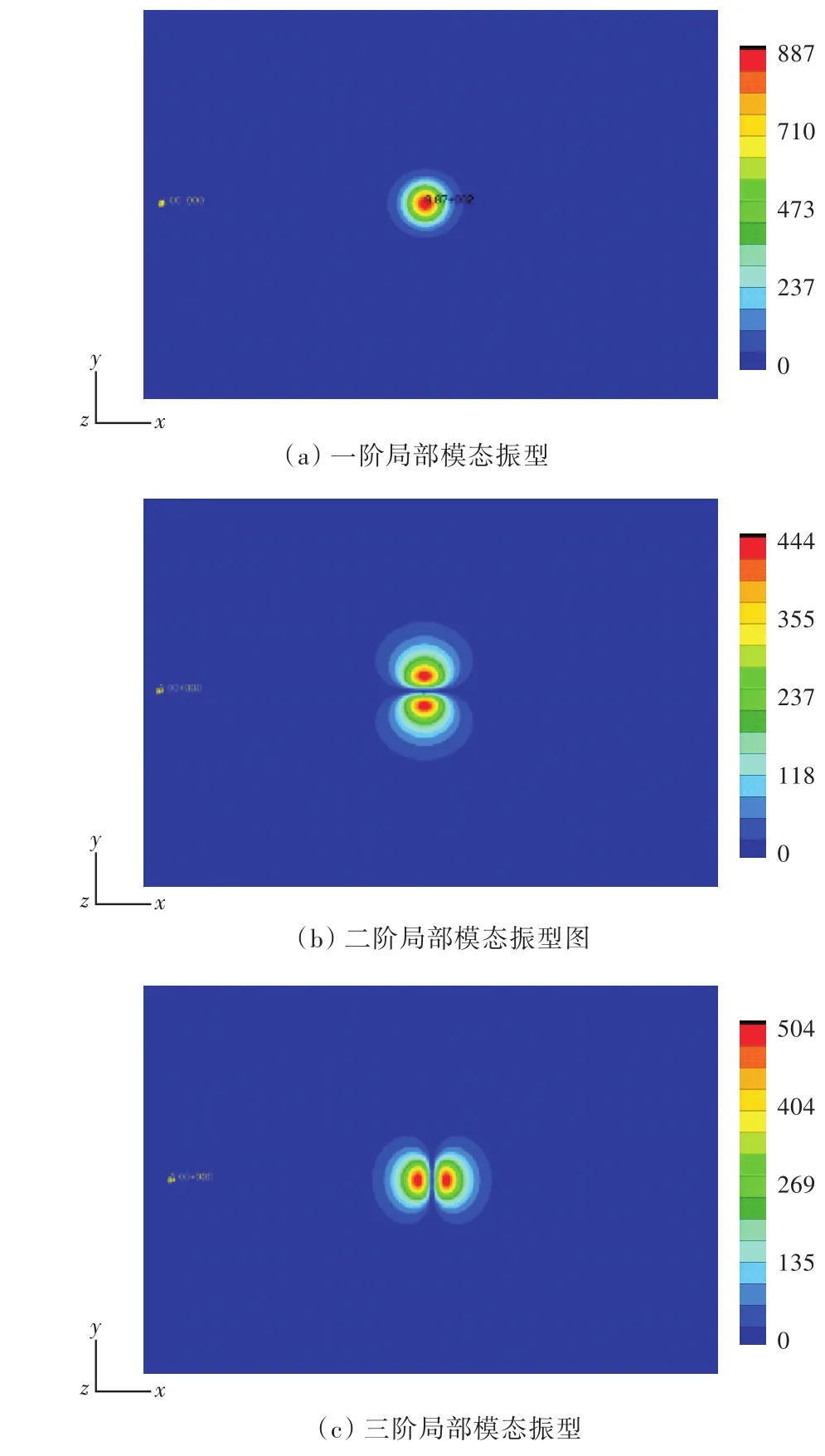
图14 板壳单元离散模型的前3阶局部模态振型图(m=2)Fig.14 The first three order local mode shapes with shell elements(m=2)
5.2 幂律变化对频率响应的影响
对幂律m=2,3,4的声学黑洞板分别进行频响分析,网格划分时黑洞区域厚度阶梯变化尺度为2 mm,计算结果如图15所示。
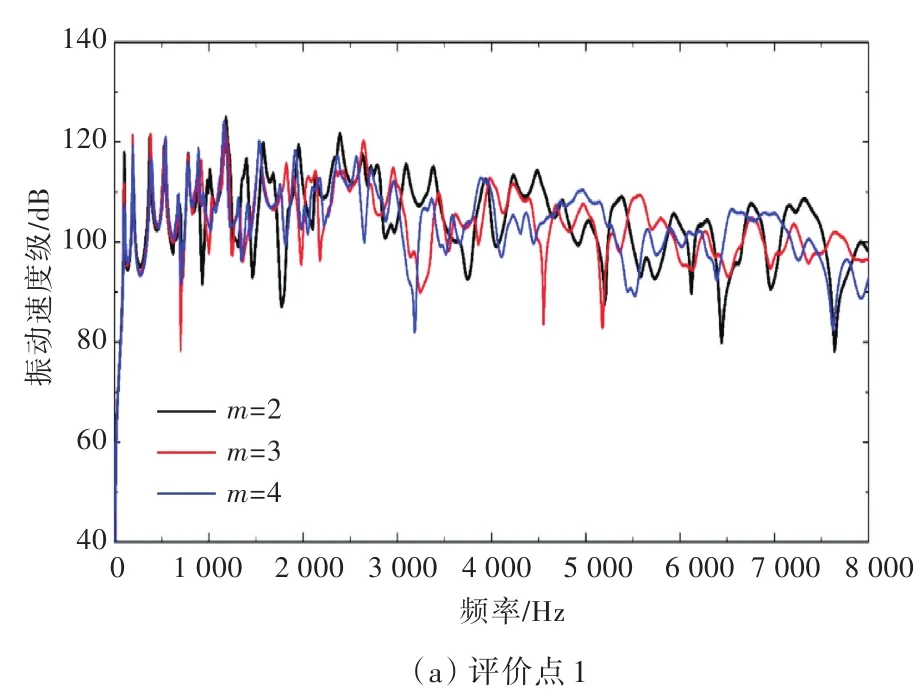
图15所示的频响分析结果表明,低频段时三者相差不大,黑洞效应不明显。在高频段,不同幂律声学黑洞板的减振频段不同,例如m=4的声学黑洞板在3 000~4 000 Hz频段的减振效果优于m=2的声学黑洞板。
6 结 论
针对内嵌二维声学黑洞薄板,本文对采用板壳单元模拟声学黑洞效应的计算方法进行数值实验计算,并与体单元的模拟结果进行了对比,验证板壳单元模拟方法的有效性。探讨了声学黑洞板厚度阶梯变化尺度以及幂律对其振动性能的影响,为声学黑洞板的设计与实际应用提供指导。研究表明:
1)采用板壳单元建模方法,声学黑洞板整体模态以及频率响应计算结果与体单元建模方法的基本相同,模态计算结果误差小于10%。板壳单元建模大大减少了模型单元数量,提高了计算效率。这证明了采用板壳单元模拟声学黑洞板的合理性和有效性。
2)声学黑洞区域的厚度阶梯变化尺度以及幂律的变化可以调节黑洞区域局部模态对应的固有频率,影响具体频段的减振效果。在实际应用中,可以利用该特点对目标频段进行减振设计。
