FeNiCrSiMoMnC合金气雾化熔滴的运动与传热行为模拟分析

2019-08-22胡云飞李景昊周香林杜开平马尧于月光

热喷涂技术 2019年2期

胡云飞，李景昊，周香林*，杜开平，马尧，于月光

（1.北京科技大学新金属材料国家重点实验室，北京 100083；2.加拿大麦吉尔大学机械工程系，蒙特利尔 QCH2A0C3；3.北京矿冶科技集团有限公司，北京 100160）

0 引言

近些年来，随着金属增材制造(MAM)、金属注射成型(MIM)及粉末冶金(PM)、冷热喷涂等行业的迅猛发展，对合金粉末的质量，特别是粒度分布、球形度、成分精度及杂质元素控制等方面的要求越来越高。气雾化法制备的合金粉末具有球形度好、粒度分布窄且易于控制、氧含量低等优点，自20世纪20年代起源以来，经过100多年的发展，现已成为制备高性能合金粉末的主要方法[1-4]。气雾化制粉过程是以高速气流冲击合金熔体，将其粉碎成小液滴并随后冷却凝固的过程；其间高速气流的动能转化为小液滴的表面能，同时拖曳熔滴一起飞行，因此是一个多相流相互耦合作用的复杂过程。熔滴在凝固之前要在雾化腔内飞行一段距离，即为熔滴的飞行过程，此过程中熔滴与气流存在热量交换。气雾化熔滴的运动与热交换环节是熔体雾化破碎到最后凝固成粉的中间过渡阶段，起到承上启下的作用，对粉体凝固组织及最终性能将产生重要影响。但气雾化过程速度很快，不易通过直接观测以准确确定过程参数，故研究工作者多采用数值模拟计算与实验相结合的方法，研究气雾化过程中各参数对粉末性能的影响[5-7]，但这些研究并未对熔滴破碎之后冷却凝固之前的速度及传热行为做分析，亦没有考虑雾化气体的初始速率的影响，而决定气体初始速率的雾化压力是雾化生产中的重要影响因素，故此方面研究还需继续加深。本文以重载耐磨耐腐蚀激光熔覆涂层用FeNiCrSiMoMnC合金为对象，着重分析气雾化制粉过程中熔滴的飞行运动过程及传热行为，并在此基础上考虑了气体初始速率的影响，建立描述相关过程的数学模型并给出相应的模拟计算结果，为进一步研究雾化熔滴的凝固组织及制备高质量合金粉体奠定基础。

1 数学模型的建立

1.1 气体与熔滴的运动模型

气雾化过程中，合金液流通过喷嘴，在雾化气体的高速冲击作用下破碎成细小熔滴，熔滴在雾化腔内一边飞行一边冷却，此过程中熔滴与周围气体环境发生明显的热量交换。已有研究者提出一些数学模型对熔滴的传热及冷却凝固行为进行预测[8-10]，但考虑到气雾化工艺本身是多相流耦合作用的复杂过程，因此需要对模型做必要的简化[11]：(1)熔滴在喷嘴出口处形成且视为刚性球体；(2)所有熔滴只沿轴向运动；(3)熔滴间无碰撞影响；(4)考虑到合金液流被高速气流破碎，熔滴初速度视为80m·s-1。

在雾化腔内，熔滴与气体的速度差引起作用在熔滴上的拖曳力，在该力的作用下，熔滴逐渐被加速，根据牛顿第二定律，可得如下熔滴速度与拖曳力的关系式[12-13]：

其中，vd，ρd分别表示熔滴速度、密度，vg，ρg分别表示气体速度、密度， g表示重力加速度，取9.8m·s-2，CD表示拖曳系数。拖曳系数可由以下经验公式求得[14]：

式中

其中Re表示雷诺数，d表示熔滴直径，μg表示气体动力粘度。为求解方程(1)，需建立气体速度与轴向距离的关系，假设熔滴的运动不影响气体速度的变化，一个较成熟的气体速度衰减方程为[15]：

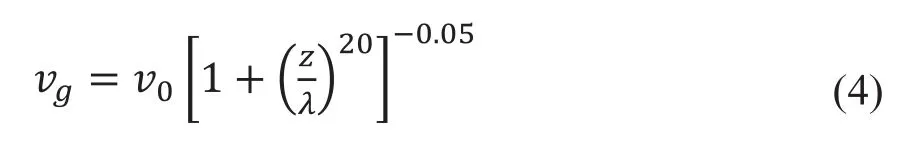
其中，v0表示气体初始速率，z表示气体轴向飞行距离，表示气体衰减系数，α是与气体特性相关的经验常数，取7.414[16]，Ae表示喷嘴喉部面积，取2.25×10-5m2。

1.2 熔滴的传热模型

熔滴在飞行过程中与周围气体环境发生热交换，其热焓变化率与熔滴温度和固相分数有关，由下式表示[17]：

式中，Cpd=CL-(CL-CS ) fs，ΔHd=ΔHf-(CL-CS )(TL-Td )，其中，Hd表示单位质量合金热焓，Td表示熔滴温度，fS表示熔滴固相分数，CL，CS，Cpd分别表示合金液态比热容、固态比热容和混合比热容，ΔHf表示单位质量合金熔化潜热，TL表示液相线温度。

在快速凝固的条件下，可忽略热辐射对熔滴温度的影响，因此熔滴与外界发生热量交换的主要形式为热对流[18]。又考虑到合金液的热传导性高，熔滴的Biot数较低（Bi=hd/λ），可以忽略熔滴内部的温度梯度[19-20]，即熔滴整体视为等温系统，对流传热只发生在熔滴与外界环境之间，则熔滴的传热过程符合牛顿传热模型，由牛顿冷却定律得[16]：

其中，Sd，Vd分别表示熔滴的表面积、体积，h表示传热系数，Tg表示气体温度。联立式(5)(6)，消去热焓微分项，得到直径为d的熔滴的温度变化表达式：

传热系数h由Ranz-Marshall公式求得[21]：

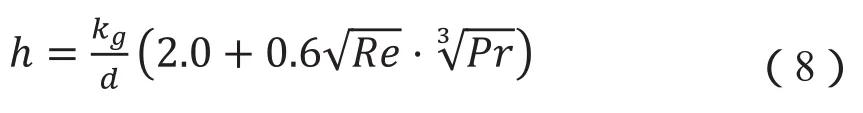
其中，Pr表示普朗特数，由式Pr=Cpgμg/kg确定，Cpg表示气体比热容，kg表示气体导热系数。

2 模型求解与讨论

模型中所用的合金材料为FeNiCrSiMoMnC，雾化气体为氮气，涉及到的参数如表1所示。因粉末粒度分布不均匀，分别选取直径为60μm、80μm、100μm、120μm、150μm的熔滴为研究对象，根据以上构建的模型，通过编程求解，可得到熔滴直径对熔滴速度、雷诺数、传热系数的影响。

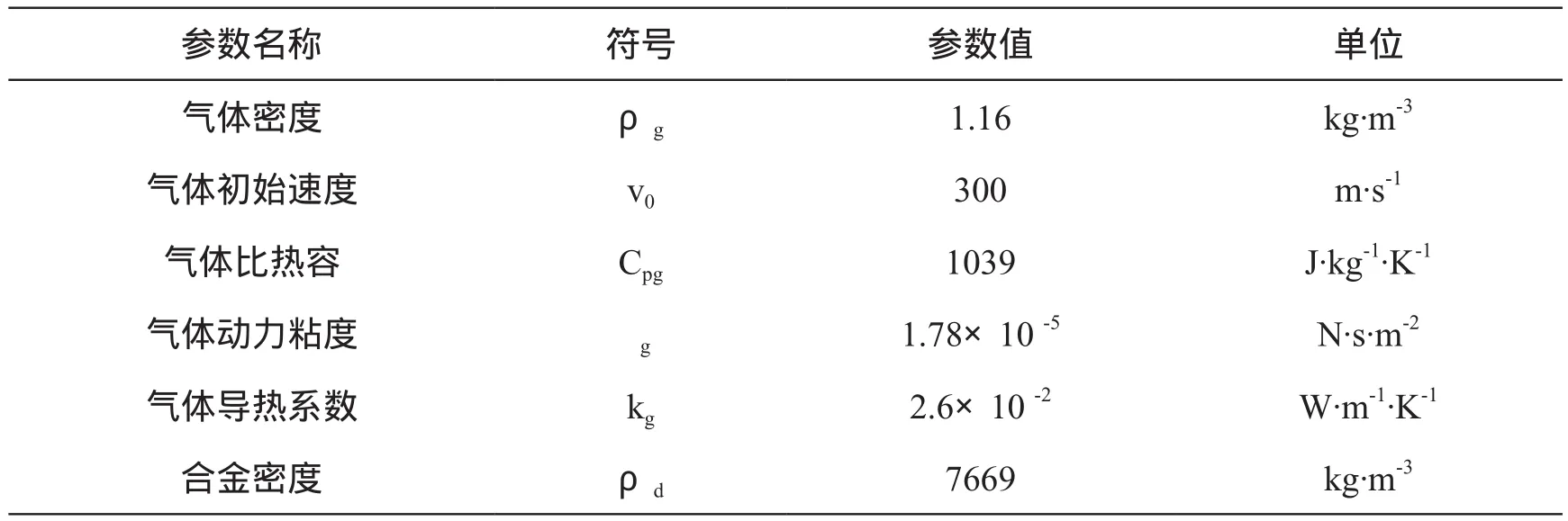
表1 合金材料及气体相关参数[15-16]Table 1 Parameters Related to Alloy Materials and Gas

熔滴速度与飞行距离的关系如图1所示，熔滴速度都是先逐渐增大，这是由于气体的拖曳作用使其加速，当熔滴与气体速度相同时，熔滴速度达到最大值，此时由于惯性与重力的作用，熔滴会继续飞行，而气体速度持续衰减，对熔滴的拖曳作用表现为减速，因此熔滴速度又逐渐减小。由于气体速度衰减很快，可以看出，不同直径的熔滴达到最大速度时的飞行距离差距很小。同时可以发现，气体对小熔滴的加速和减速作用都较明显，这是因为，由式(2)(3)可知，熔滴直径为影响雷诺数的一个主要因素，直径越小，雷诺数越小，则拖曳系数越大，即气体对熔滴的拖曳作用越明显，所以小熔滴加速较快，最大速度较大，减速也较快，甚至于后期小熔滴速度已经小于大熔滴速度。若考虑到此过程中熔滴的碰撞，则小熔滴可能会嵌入大熔滴内部成为异质形核的核心，或嵌在大熔滴表面并在冷却凝固后形成卫星粉。

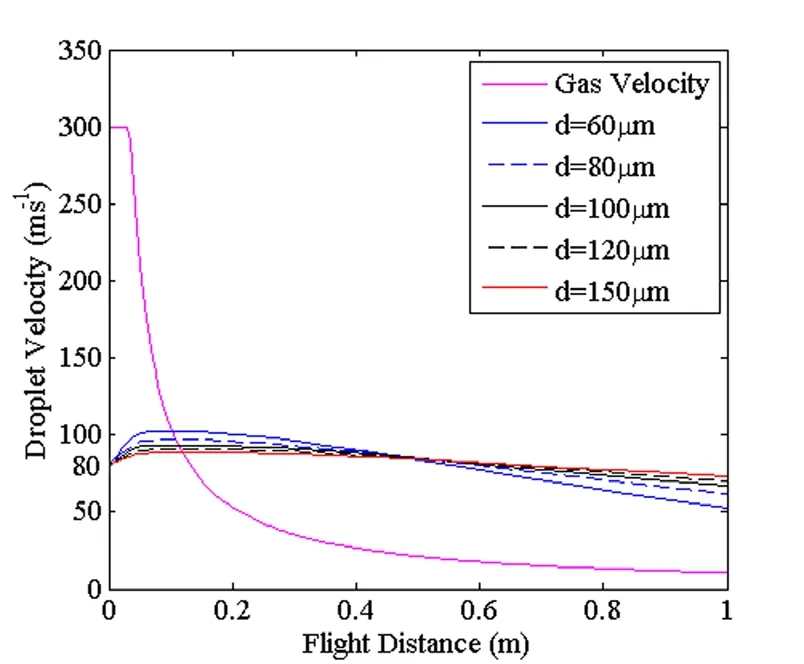
图1 熔滴速度与飞行距离的关系Fig.1 The relation between Droplet Velocity and Flight Distance

当综合考虑熔滴速度与直径因素时，雷诺数与飞行距离的关系如图2所示。开始由于气体速度基本不变，雷诺数下降较慢，当气体速度急速衰减时，雷诺数呈现出相同的趋势，即迅速减小，且在熔滴最大速度点处达到最小值，由式(3)可知，该最小值为0，而后又随熔滴与气体相对速度的增大而增大。

图2 雷诺数与飞行距离的关系Fig.2 The relation between Reynolds Number and Flight Distance

传热系数是衡量熔滴与雾化气体传热快慢的重要物理量，其值是和熔滴与气体相对速度正相关的函数，与飞行距离的关系如图3所示。初始阶段，由于熔滴与气体相对速度最大，所以传热系数也为最大值，随相对速度的减小，其值逐渐减小，当熔滴与气体速度相等时，雷诺数为零，由式（8）可知，传热系数达到最小值2kg/d，后又随相对速度的增大而增大。

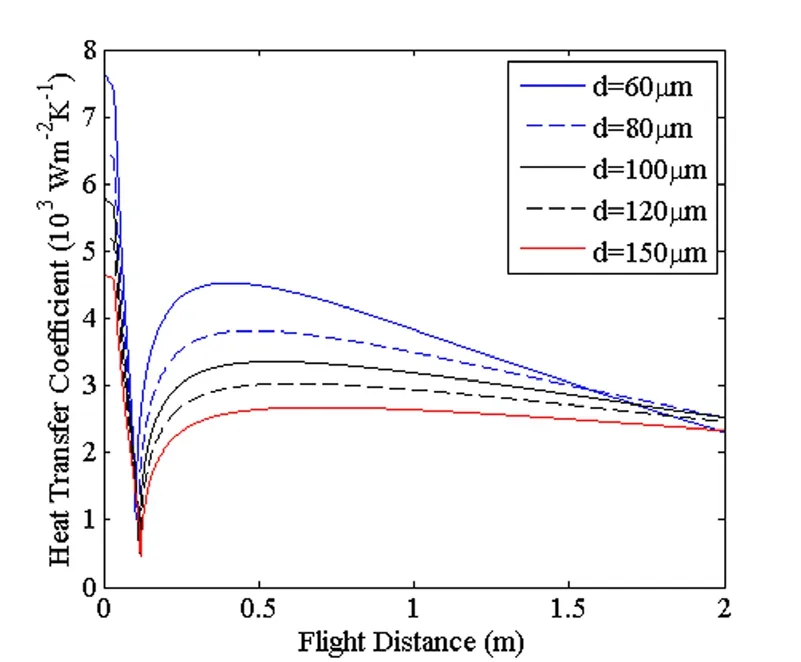
图3 传热系数与飞行距离的关系Fig.3 The relation between Heat Transfer Coef fi cient and Flight Distance

雾化压力是气雾化生产中重要的工艺参数，主要表现为影响气体的初始速率，本文模拟中通过改变气体初始速率来分析雾化压力对熔滴的影响，熔滴直径固定为100μm，如图4所示。图中虚线为气体速度衰减曲线，相同颜色的实线为该气体初始速率下的熔滴速度变化曲线，气体初始速率越大，熔滴所能达到的最大速度越大，达到最大速度时熔滴的飞行距离更大，但该差距很小。传热系数和熔滴与气体的相对速度有关，如图5所示，基本走势还是从一开始的最大值逐渐减小至极小值2kg/d，然后再逐渐增大，但气体初始速率越大，熔滴与气体的相对速度越大，故开始阶段传热系数较大，且由于相对速度为0时熔滴飞行距离更大，故传热系数达到极小值的飞行距离也相应变大。