一道耐人寻味的面积问题*

(金陵中学河西分校，江苏 南京 210019)

某数学教研群研讨了一道题目如下：

题目如图1，在△ABC中，∠ACB=90°，AC=BC，∠ADC=45°，S△ADB=6，求AD的长．

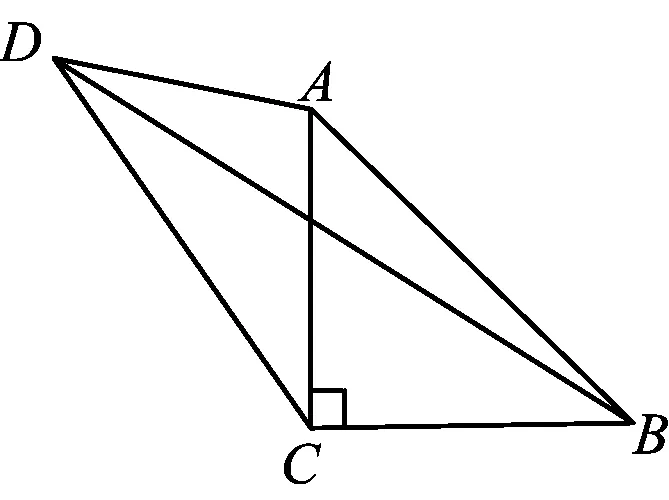
图1

与常见的题目不同，此题没有给出任何一条线段的长度，求解的难度不言而喻．从哪里入手呢？探究解法，耐人寻味．

最自然的想法：作△ADB的高BH，能直接求解吗？还需要再做些什么？

解题模型的暗示:遇到等腰直角三角形，可将△ACD绕点C顺时针旋转45°，或将△BCD绕点C逆时针旋转45°，能直接求解吗？还需要再做些什么？

解题经验的积累:面积问题，还能从哪些角度思考？

1 直接作高

解法1如图2，过点B作BE⊥AD交DA的延长线于点E，过点A作AF⊥CD于点F，则

∠AEB=∠AFC=90°，

且

因为∠EAC=∠EAB+45°=∠ACD+45°，所以

∠EAB=∠ACD，

从而

△EAB∽△FCA，

可得

于是

进而

BE=AD.

又因为S△ADB=6,所以

故

评注仅仅作高BE是不够的，从∠ADC=45°联想构造等腰直角三角形解决问题．

图2 图3

解法2如图3，过点B作BE⊥AD交DA的延长线于点E，在AE的延长线上取点F使得EF=BE，则

因为∠FAC=∠FAB+45°=∠ACD+45°，所以

∠FAB=∠ACD，

从而

△FAB∽△ACD，

可得

于是

故

BE=AD.

又因为S△ADB=6,所以

故

评注仅仅作高BE是不够的，利用“∠BAC=∠ADC=45°”构造“一线三等角”模型，借助相似三角形知识解决问题．

2 间接作高

分析如何利用好题设∠ADC=45°是解决本题的关键，其中构造等腰直角三角形是常用策略．

解法3如图4，过点C作CE⊥CD交DA的延长线于点E，联结BE，则

∠DEC=∠EDC=45°，CE=CD，

∠DCE=∠ACB，

从而

∠BCE=∠ACD.

又

BC=AC，

于是

△BCE≌△ACD(SAS)，

可得

BE=AD， ∠CEB=∠ADC=45°，

进而

∠BEA=90°，

即

BE⊥DE.

因为S△ADB=6，所以

故

评注构造等腰直角三角形间接得到△ABD的高BE，并且BE=AD，问题得解．若辅助线改为“将△ACD绕点C顺时针旋转45°”，则需证明点D,A,E在一条直线上，比较麻烦．

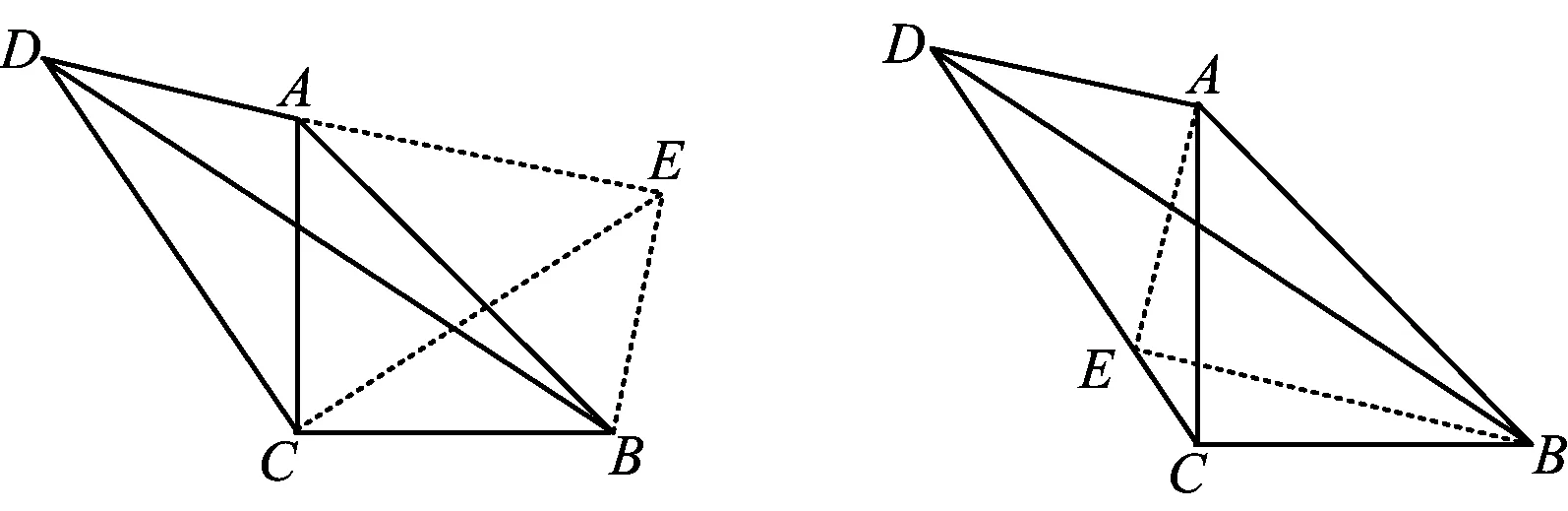
图4 图5

3 等积转化

解法4如图5，过点B作BE∥AD交CD于点E，联结AE，则

∠BEC=∠ADC=45°=∠BAC，

从而点A,E,C,B共圆，可得

∠AEB=∠ACB=90°，

于是

∠DAE=90°，

即

AE⊥AD且AE=AD.

因为BE∥AD，所以

S△ADE=S△ADB=6，

即

故

评注作平行线实现△ADB面积的等积转化，意外获取等腰直角三角形解决问题，令人拍案叫绝．

解法5如图6，过点C作CE⊥CD，且CE=CD，联结AE，则

∠DEC=∠CDE=45°， ∠ADE=90°.

易证△ACE≌△BCD(SAS)，从而

AE=BD， ∠AEC=∠BDC，

于是

∠AED=45°-∠AEC=45°-∠BDC.

作BF∥AD交DE于点F，则BF⊥DE，可得

∠DAE=90°-∠AED=45°+∠BDC=∠FDB，

从而

Rt△DAE≌Rt△FDB(AAS)，

于是

DF=AD.

因为BF∥AD，所以

S△ADF=S△ADB=6，

即

故

评注利用已有的等腰直角三角形，作等腰直角三角形，构造全等三角形，再作平行线实现△ADB面积的等积转化，意外获取等腰直角三角形解决问题．

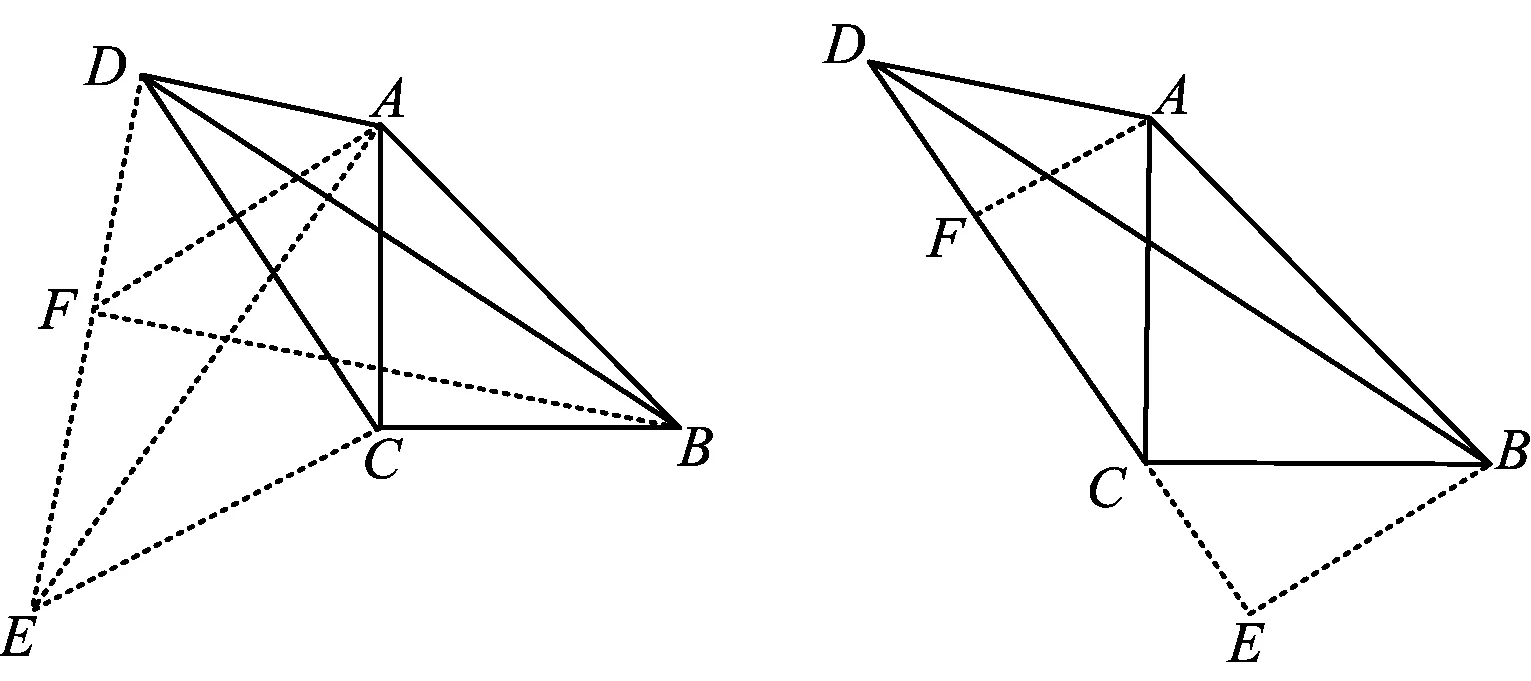
图6 图7

4 和差转化

解法6如图7，过点B作BE⊥CD交DC的延长线于点E，过点A作AF⊥CD于点F，则AF=DF.易证△BCE≌△CAF(HL)，从而

BE=FC，AF=CE.

设AF=DF=CE=m，FC=BE=n，则

S△ABD=S△ADF+S四边形AFEB-S△DEB，

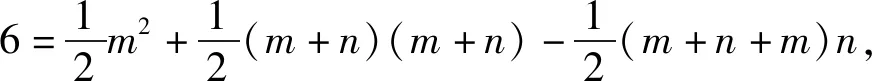
解得

m2=6，

从而

于是

评注利用面积的和差关系，实现△ADB面积的转化是解决面积问题的常用方法．

5 相似转化

解法7如图8，以BD为斜边作等腰Rt△DBE，联结CE，则

从而△ABD∽△CBE，可得

及

因为∠BAC=∠ADC=45°，∠ACB=90°，所以

∠DAB+∠ACD=180°，

即

∠ECB+∠ACD=180°，

进而

∠DCE=180°-90°=90°.

作CF⊥BE于点F，易证△CED∽△FCE，从而

即

CE2=DE·CF，

从而

故

评注利用已有的等腰直角三角形，作等腰直角三角形，构造旋转相似三角形，实现△ADB面积的转化也是解决问题的一种有效方法．

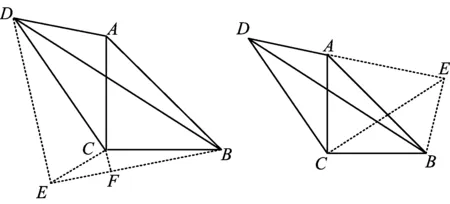
图8 图9

变式1如图9，在△ABC中，∠ACB=90°，AC=BC，∠ADC=45°，AD=6，求△ABD的面积．

解如图9，过点C作CE⊥CD交DA的延长线于点E，联结BE，则

∠DEC=∠EDC=45°，CE=CD，

∠DCE=∠ACB,

从而

∠BCE=∠ACD.

又

BC=AC，

于是

△BCE≌△ACD(SAS)，

可得

BE=AD=6， ∠CEB=∠ADC=45°，

进而

∠BEA=90°，

即

BE⊥DE，

故

变式2如图10，在△ABC中，∠ACB=90°，∠ABC=60°，∠ADC=30°，AD=6，求△ABD的面积．

解如图10，过点B作BE∥AD交CD于点E，联结AE，则

∠BEC=∠ADC=30°=∠BAC，

从而点A,E,C,B共圆，可得

∠AEB=∠ACB=90°，

于是

∠DAE=90°，

即

AE⊥AD，

且

因为BE∥AD，所以

图10 图11

变式3如图11，在△ABC中，∠ACB=90°，∠ABC=α，∠ADC=β，α+β=90°，AD=m，求△ABD的面积．

解如图11，过点C作CE⊥CD交DA的延长线于点E，联结BE，则

∠ECB=∠DCA.

又

从而

△BCE∽△ACD，

可得

∠CEB=∠CDA，

且

于是

BE=mtanα.

因为∠CDA+∠DEC=90°，所以

∠CEB+∠DEC=90°，

即

∠DEB=90°，

从而

BE⊥DE，

于是

评注变式1～3均可以尝试用多种解法解决，限于篇幅，本文不再赘述．

解题的“旅行”虽然短暂，但沿途的“风景”尽收眼底，美不胜收，“小题大做”值得珍藏．