换个顺序 先算后代 简化运算*
2019-08-19
(姜堰第二中学,江苏 泰州 225500))
文献[1]指出简化解析几何的运算一直是解析几何研究的重点,并提出两个视角,即几何视角和代数视角.文献[2]通过“先定后证”从代数视角有效地简化了解析几何中定点定值问题的运算.文献[3]给出5种策略:设而不求、巧用几何性质、合理翻译条件、利用常见结论、争取整体替代.而实际上,繁分式的运算与化简才是解析几何运算的难点,如何简化此类运算才是广大师生的共同追求,由此笔者进一步提出解决策略:换个顺序,先算后代,简化运算.

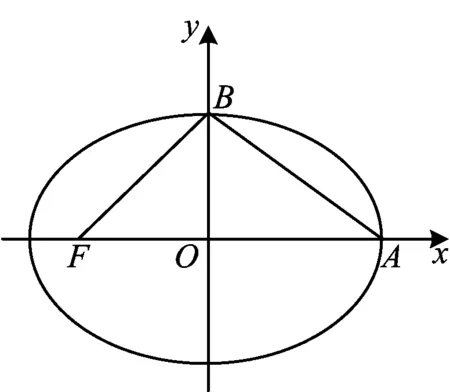
图1
2)已知△ABF外接圆的圆心在直线y=-x上,求椭圆的离心率e的值.
(2019年江苏省数学高考模拟试题第17题)
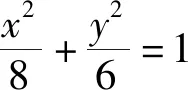
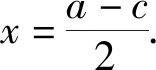
由点C在线段AB的中垂线上,得
整理得
b(a-c)+b2=ac,
即
(b-c)(a+b)=0.
因为a+b>0,所以b=c,故椭圆的离心率
评注此为常规思路,在得到点C的坐标后,直接代入线段AB的中垂线方程进行运算,虽然整体运算量不大,但仍可以换个顺序,先算后代,简化运算.
第2)小题另解因为△ABF外接圆的圆心在直线y=-x上,所以可设△ABF的外心为C(x0,-x0),由外心的性质知点C在线段AF的中垂线上,且满足AC=BC,则
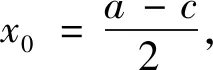
(1)
且
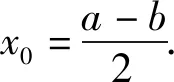
(2)
由式(1)和式(2)可得b=c,
故
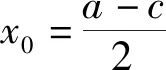
例2已知⊙C的方程为(x+1)2+y2=1,过y轴正半轴上一点P(0,2)且斜率为k的直线l交⊙C于点A,B,当△ABC的面积最大时,直线l的斜率k=______.
思路1直线l的斜率存在且直线l的方程为y=kx+2,即kx-y+2=0,从而
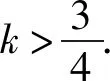
至此陷入运算的困境,要得到最终答案,还得费一番心思.
思路2直线l的斜率存在且直线l的方程为y=kx+2,即kx-y+2=0,代入圆的方程(x+1)2+y2=1,得
(k2+1)x2+2(2k+1)x+4=0.
设A(x1,y1),B(x2,y2),则
又
Δ=[2(2k+1)]2-16(k2+1)>0,
从而

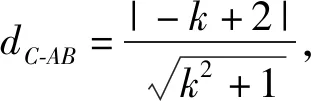
与思路1一样,想得到最终答案也不容易.
评注上述两个常规思路均将△ABC的面积表示为关于斜率k的函数,但由于函数表达式过于复杂,不易求得最大值.这就暗示我们要进行换位思考,用另外的变量来表示△ABC的面积,在求得最大值后,再去求相应的斜率.
解法1直线l的斜率存在且直线l的方程为y=kx+2,即kx-y+2=0,从而
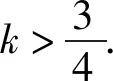
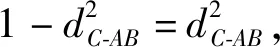
解法2设∠ACB=θ(其中0<θ<π),则

说明思路1与思路2均将△ABC的面积直接表示为斜率k的函数,但函数表达式过于繁琐,最大值不好求.在重新调整思路后,借助不同于斜率k的变量(点C到直线AB的距离dC-AB或∠ACB)建立了新的函数,其表达式简洁,易于求得最大值.在S△ABC取得最大值的条件下很快求得相应的斜率的值,快速达成问题的解决.这里运用了“换个顺序,先算后代”的策略,大大简化了运算.
实际上,思路1和思路2的问题在于运算得太彻底,其实中间的运算步骤已经能解决问题,调整如下:

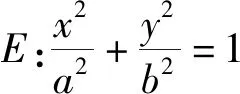
1)求椭圆E的标准方程.
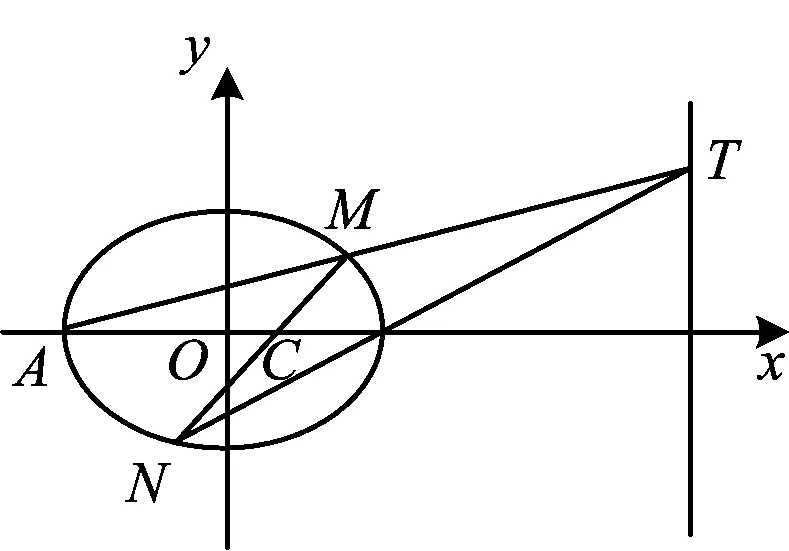
图2
2)如图2,设A为椭圆E的左顶点,过点C(1,0)的直线与椭圆E交于点M,N,直线AM与直线l:x=9交于点T,问:直线TN是否过定点?若过定点,求出定点坐标;若不过定点,请说明理由.
思路1这是定点问题,常规思路是先设后求.
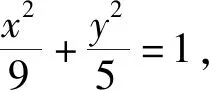
(5+9k2)x2-18k2x+9k2-45=0,
从而
于是
x1x2=5(x1+x2)-9.
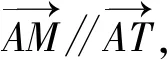
从而
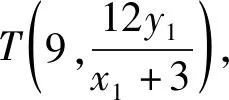
故直线NT的方程为
即
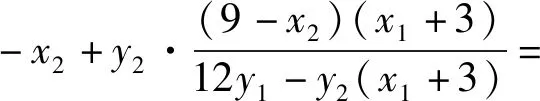
亦即直线NT的方程为
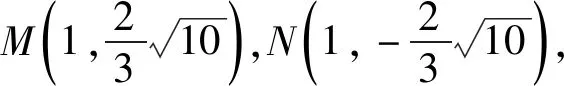
综上可知直线NT过定点(3,0).
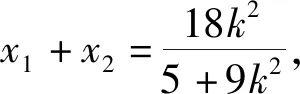
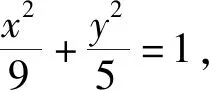
(5m2+9)y2+10my-40=0,
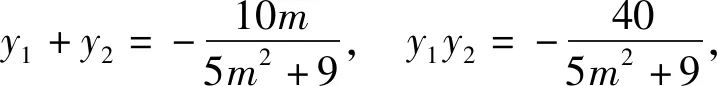
于是
4(y1+y2)=my1y2.
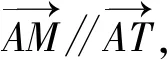
从而
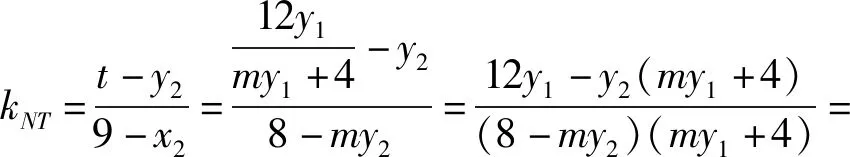
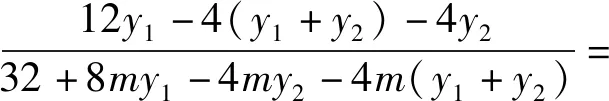
于是直线NT的方程为
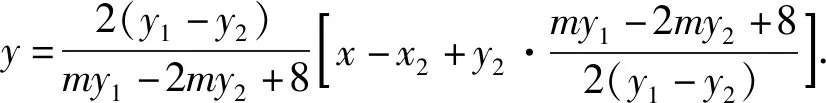
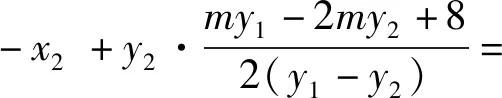
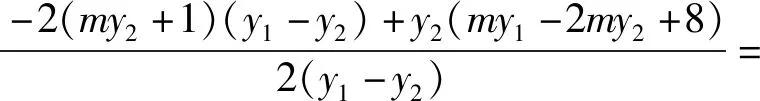
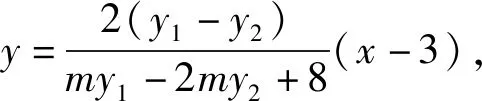
故直线NT过定点B(3,0).
评注设直线NT的方程为x=my+1,可以减去斜率不存在的讨论,运算量也稍简单一点.当然,与前面一样,要不是4(y1+y2)=my1y2的帮忙(注:此式的得来要比x1x2=5(x1+x2)-9容易多了),也会很麻烦.
思路3既然此题为定点问题,也可用文献[2]先定后证的方法简化运算.


(5m2+9)y2+10my-40=0,
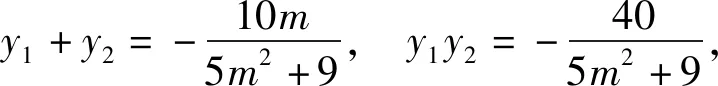
于是
4(y1+y2)=my1y2.
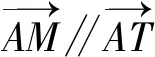
于是
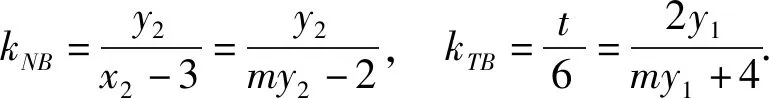
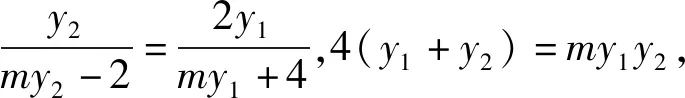
说明在实施先定后证后,运算量确实大大减少,思路1和思路2能改进吗?
思路1和思路2在实施先设后证时,均遇到了繁分式的运算与化简问题,并且运算量极大,相当困难,要不是两根之和与两根之积的巧妙转化,还不知要算到何时?下面同样运用先算后代的策略来大大简化运算.
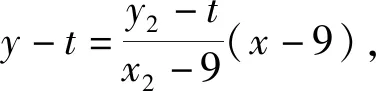

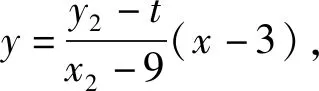
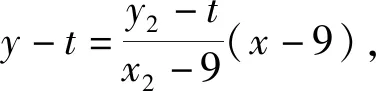
从而
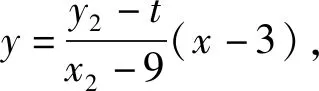
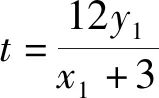
简化运算始终是解析几何的主旋律,代数与几何是两大主方向.这里从代数恒等变换的角度提出“换个顺序,先算后代”的策略,给出了一种新的简化解析几何运算量的策略.这是一种全新的解题体验,也是对文献[3]提出的5种经典策略的有力补充.当然,追求永无止境,希读者做更开阔的探索与研究.
