牙轮钻头单金属密封数值模拟与优化

宋保健,邹 春，孙 凯，明 鑫，任武化

(1.中石化中原石油工程有限公司，河南 濮阳 457001；2.中石化中原油田分公司 濮东采油厂，河南 濮阳 457001；3.中石化中原石油工程有限公司 钻井一公司，河南 濮阳 457001；4.中石化中原石油工程有限公司 管具公司，河南 濮阳 457001；5.青海油田机械厂，甘肃 敦煌 736202)

牙轮钻头是油气勘探过程中重要的破岩工具，随着钻井深度的增加，井底高压和振动工况使得钻头的寿命受到极大的影响，而钻头中的动密封可以阻止外部钻井液侵入轴承内部，从而延长轴承的寿命[1-2]。在钻进过程下，由于密封腔中的润滑油不能及时地从地面进行补给，因此钻头动密封工况要比常规工业领域的动密封更加恶劣，间接造成牙轮钻头的寿命较短。目前钻头动密封主要包括金属型密封和橡胶型密封。金属密封(如图1)主要靠两个金属环间一层极薄的油膜来保证动密封的正常工作[3-4]，为钻头轴承的寿命提供保障。张宝生[5]、张毅[6]结合有限元仿真和正交实验法对单金属密封的橡胶支撑环硬度和部分结构参数进行了优化研究，分析结果表明该优化方法可以显著地降低密封面的接触压力。钻井现场的钻头失效情况表明，钻井液中的微小磨砺很容易侵入到金属动密封的接触面，造成润滑油的大量泄漏，即便是对密封面进行特殊涂层处理，密封面的磨损依然比较严重(如图2)。因此，如何在保证密封泄漏率的情况下尽可能降低密封面的最大接触压力是非常重要的，本文对真实工况下的单金属动密封进行了数值仿真分析，并结合密封泄漏率求解和响应面方法对密封的泄漏率进行优化。

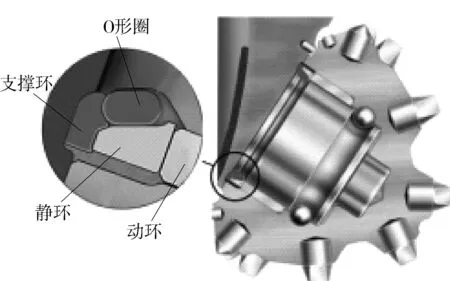
图1 牙轮钻头单金属密封

图2 单金属密封失效

1 单金属密封有限元分析

1.1 有限元分析

在不考虑密封倾斜的情况下，单金属密封可以近似认为是轴对称模型，因此可以将有限元模型简化为二维轴对称模型，考虑环空钻井液压力和密封内部润滑油压力后的有限元模型如图3所示。根据参考文献[7]，钻头内部润滑油和外部泥浆之间的压差约为0.3～0.7 MPa，本文分析中密封内侧外压差为0.3 MPa，加载在密封外侧的钻井液压力为20 MPa。该工况下的动密封接触压力如图4所示。

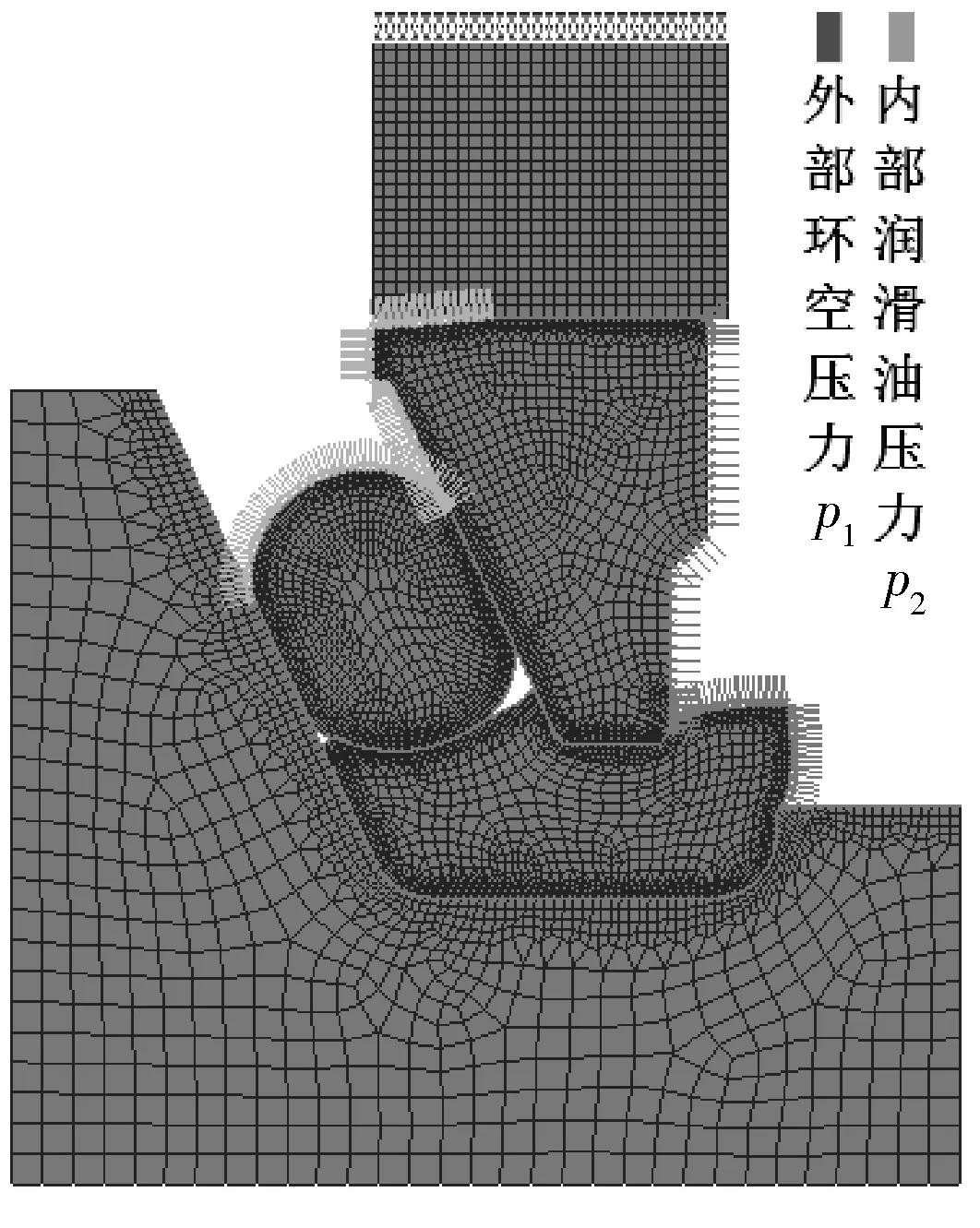
图3 施加载荷后单金属密封有限元模型

图4 高压工况时单金属密封接触应力

根据分析结果可以看出，动密封面的接触应力从内侧到外侧逐渐降低。由于高压环境压力的作用，接触应力最大值处于密封面内侧的楔入角处，约为66.14 MPa。由于内侧接触应力较大，虽然可以保证动密封面具有较大的接触比压，避免了润滑油泄露，但同时也会造成动密封面间不易于形成稳定的油膜；由于外侧接触压力较低，钻井液中的微小颗粒极易进入动密封面，从而使得密封面形成犁状沟槽。同时，静环与橡胶O形圈之间的接触压力并不高，因此橡胶O形圈易产生相对滑动，造成橡胶O形圈的磨损，降低静环与O形圈的静密封性能。由于橡胶支撑环与静环的倒角处出现了接触应力集中，当静环在井底振动作用下发生上下移动时，橡胶支撑环的上部接触区域将会被压溃。

1.2 密封泄漏率求解

由文献[8]可知，通过逆解法对动密封面的油膜厚度进行求解可以提高计算效率，同时还能满足工程需求。本文对动密封面泄漏率的求解，需要对计算模型进行以下假设：

1) 润滑油的密度和黏度恒定且为不可压缩流体。

2) 金属环表面的粗糙度对动密封面动压润滑效应没有影响。

3) 井底温度对金属密封面润滑状态无影响。

4) 动密封面的接触应力分布与密封面之间润滑油的压力分布基本一致。

单金属密封动密封面间的油膜厚度分布可以由Reynolds方程求出，由于不考虑密封面粗糙度的影响，因此二维雷诺方程可以简化为：

(1)

式中：h为润滑油油膜厚度；η为润滑油动力黏度；p为金属密封面接触压力；u为动静环的相对边界移动速度。

由于单金属密封为二维模型，因此可以认为动密封面的油膜厚度在周向上保持一致，则雷诺方程可简化为：

(2)

根据式(2)确定动密封面的油膜厚度和压力分布后，金属动密封的泄露率可以表示为：

(3)

本文在有限元数值模拟的基础上，先求出动密封面的接触压力梯度分布情况，再求出密封面润滑油膜的分布情况；当接触压力梯度达到最大值时，密封面的油膜厚度取最小值hmin，进而求得最小油膜厚度处密封面的泄漏率。

2 动密封泄漏率响应面优化分析

2.1 响应面回归模型建立

单因素变量分析仅仅改变一个设计变量而得到的优化结果，考虑不全面，有一定的局限性。本文将利用响应面优化方法对单金属密封进行多因素交互优化。响应面优化方法是通过物理或仿真实验得到足够的实验数据，合理利用试验设计方法，通过二次回归方程，拟合出多个变量与响应目标间的函数表达式，采用对回归方程的分析得到最优响应目标对应的参数组合[9]。根据单金属密封的设计经验，本文选用静环端面的接触宽度、静环内侧斜面倾角及静环高度这三个变量作为设计变量，而将动密封的泄漏率作为优化目标，根据试验原理，采用三因素三水平的响应面模型进行分析[10]，如表1所示。

表1 试验因素与水平

根据正交设计软件，可以得到17组不同的参数组合。在此基础上结合有限元仿真分析，得到每组参数组合对应的密封面接触压力，再根据密封泄漏率计算方法，得到每组参数对应下的动密封泄漏率。根据Box-Behnken设计方法，采用二次回归模型拟合17组仿真实验数据，依据最小二乘法即可求得动密封响应面模型中的回归系数，密封泄漏率的响应回归模型方程可以表示为：

(4)

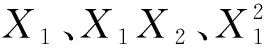
表2 泄漏量响应面二次模型方差分析

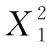
同时，根据计算结果可以得到这三个变量交互作用下对泄漏率的影响，如图5。由图5可以看出，随着密封端面接触宽度的增大，密封泄漏率也逐渐增大，初期阶段静环高度对泄漏率影响比较小，但当端面接触宽度大于3.5 mm时，泄漏率随着静环高度的增加而减小；随着接触宽度的增加，斜面倾角对泄漏率的影响并不明显，但在不同的静环高度影响下，斜面倾角对泄漏率的影响要大一些，当斜面倾角和静环高度均为最小时，泄漏率达到最大值，此时这两个因素之间的交互作用最为明显。

图5 三个变量交互作用对泄漏率的影响

3 结果优化与对比分析

为了得到最小泄漏率对应的最佳组合参数组合，需要求解出泄漏率的二次回归模型方程。借助罚函数法能将多目标优化问题中的一些优化目标设定一定的允许范围，将该优化问题简化成了单目标优化问题，也就是将复杂的优化问题转化成了多个约束条件下的简单优化问题。为了避免密封面的磨损失效，根据密封的实际工况和材料许用参数，单金属密封材料的许用使用psv值为60 MPa·m/s(ps为润滑油的压力，v为速度)。根据该许用值，当动密封的转速为300 r/min，密封面的平均直径为60 mm时，ps的峰值接触应力约为67 MPa。根据此条件可以将该优化问题可以转化为单目标优化问题[11-12]：

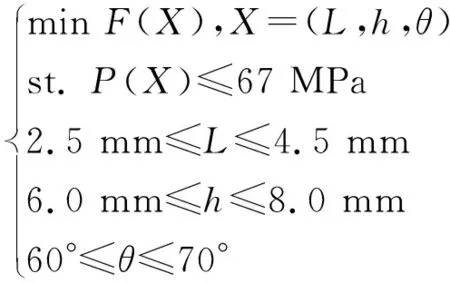
(5)

借助优化软件Design-Expert 8.0中的优化模块，优化目标函数F(X)及对应的参数值可以被计算出来。

在该优化方案设定的结构参数变动范围内，经过17次迭代，能得出17组优化目标值及相应的结构参数组合，然后将期望值最高的密封结构参数模型和初始的密封结构模型分别进行有限元计算，可以得到对应的密封面最大接触压力与泄漏率，对比情况如表3所示，可以看出优化后动密封的泄漏率降低了0.104 6 mm3/s，比优化前降低了约35.98%，同时密封面最大接触压力也比优化前的模型降低了约15%，可以有效地减缓密封面的磨损，延长密封的寿命，并且优化后的密封面最大接触压力也小于材料允许的许用最大接触压力。同时也说明了响应面方法在单金属密封泄漏率和接触压力优化中的可行性[12]。

表3 优化前后的结果对比分析

优化后的动密封接触压力分布如图6所示，优化后静环内侧楔入角处的应力集中现象有了明显改善，最大接触压力由初始模型中的66.14 MPa下降至优化后模型的56.77 MPa，有利于密封腔内润滑脂进入密封面，起到较好的润滑作用，避免了密封面内侧的磨损；同时，可以看出密封端面外侧的接触压力有所升高，从而使得密封端面接触压力分布更加均匀，能够更好地阻止钻井泥浆中的微小颗粒进入到密封端面。因此，经过优化单金属密封的结构参数，能有效地改善密封面的接触压力分布，有助于提高密封面的密封性能[12]。

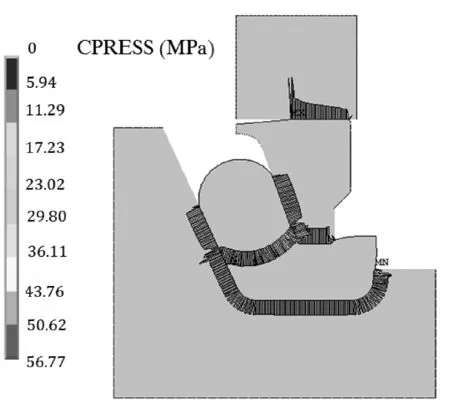
图6 优化后接触压力场分布云图

4 结论

1) 钻井工况对牙轮钻头单金属动密封的性能影响比较大，振动环境下密封面容易卡入微小磨砺，造成密封面的损伤，同时橡胶支撑垫也容易发生滑移，钻头动密封设计需要综合评价密封面的磨损和润滑脂的泄漏。

2) 高压工况下单金属密封面的接触应力呈现从内侧到外侧逐渐降低的形态，在动密封工作初期时导致密封面内侧快速磨损，同时泥浆中的磨砺性颗粒易侵入动密封面，造成润滑脂的泄露；静环内侧下部倒角处会出现接触应力集中的现象，易导致橡胶支撑环发生挤压变形；

3) 响应面法优化分析结果表明，在20 MPa的环境压力下，优化后单金属密封的性能可以得到有效改善，密封端面的最大接触压力比优化前降低了约15%，密封端面的接触压力分布也更为均匀，密封泄漏率比优化前结构降低了约36%，响应面优化法可以有效地解决单金属密封接触压力和泄漏率的多目标优化问题。