伽马阵列气液两相流截面含气率测量成像研究

赵月前，尹 丰，孙 钦，潘艳芝，3，文鹏荣，刘惜春

(1.海默科技(集团)股份有限公司，兰州 730010；2.中海油研究总院有限责任公司，北京 100028； 3.西安交通大学 动力工程多相流国家重点试验室，西安 710049)

自20世纪80年代开始，由于油气开发工程的迫切需要，油气水多相流计量技术逐渐引起广泛关注，国内外许多科研机构乃至企业对其进行了大量的研究[1-2]。目前，经过验证的具备实用价值的多相流计量技术较多，主要分为分离计量和非分离计量2大类。其中分离计量由于需要巨大的分离设备，成本高昂并且时效性差，所以非分离计量已经成为主流的多相流测量技术研究方向，而其中基于伽马射线的测量方法及对应的多相流量计产品目前应用最为成熟[3-4]，计量精度也最高，该类产品已获得大量安装应用。

水下流量计作为一款重要的水下工程装备，可以实时反映单井油、气、水的产量以及油气比、含水率等重要信息，对水下油气田开发及生产管理的全自动化具有重要意义[5-7]。水下流量计通常安装在水下采油树上，可在线监测油气田产量，为油气藏管理优化提供基础数据[8-9]。国际主流的水下流量计一般是基于伽马射线技术，即在竖直管道安装单颗放射源，通过产生的单束伽马射线进行测量。但是，该方法要求设备必须竖直安装，且最好在设备上游安装盲三通或类似的流体混合器，对油气水多相流进行混合，以达到三相分布均匀的目的。故该类设备测试精度或多或少受制于流体在管道内的分布状态，即流型流态的变化可能影响测量精度。

鉴于水下流量计超长设计寿命(一般要求大于20 a)，且要适应恶劣的水下环境，故其可靠性和测量精度是至关重要的[10]。当水下流量计采用伽马射线来测量气液两相流的相分率时，为了提升其相分率测量性能和可靠性，有必要研究伽马射线成像的机理和可行性。

马敏等人[11]研究了基于241 Am放射源的伽马阵列多相流在线检测系统，但其探测单元采用了5颗能量为59.5 keV的241 Am放射源均匀分布于管道截面，实现实时同步检测，虽然该系统具有一定的有效性，但较高的成本和复杂的辐射防护对该系统的工业化应用有较大影响。基于另外一些技术的成像系统[12]，由于测量精度低于伽马射线技术，不在本文研究范围内。

为了研究一种操作简单、成本低的伽马阵列成像系统，本文将借助CFD等工具及数值模拟方法，模拟基于单颗放射源的伽马阵列测量气液两相流截面含气率的成像过程，在考虑测量管道的竖直和水平2种布置方向，以及不同的探测器发射及接收角度的情况下，优化设备结构，并推导了伽马阵列截面含气率测量成像算法模型，为后续基于伽马阵列成像技术的水下流量计的开发应用奠定基础。

1 伽马阵列成像机理

常规伽马射线流量计是利用伽马射线透射衰减原理，在管道的一侧放置射线源，产生足够穿透整个管道直径的射线，在管道另一侧相对位置放置射线接收装置，探测衰减后的射线，透射信号的强度可以反映管道内多相流介质对射线的吸收衰减程度，从而判断管道截面相含率。现有伽马射线流量计通常都是一对或者两对发射、接收装置，空间均匀性上有较大局限。

针对气液两相流截面含气率复杂多变的现状，本文提出了一种伽马阵列测量管道截面含气率成像方法，如图1所示。在常规伽马射线流量计的文丘里管入口附近竖直方向某角度设置一个射线发射装置，然后在管道对面分别依次以某角度布置多个接收装置，形成伽马射线阵列分隔管道截面内多相流体，通过求解多对射线交点处含气率后进行图像重建，即可获取管道该处截面含气率成像。

图1 伽马阵列成像测量原理

2 伽马阵列成像模拟

2.1 测量管道摆放位置选择

为建立水下流量计成像算法模型，需先研究如何摆放水下流量计，以使截面气液分布更有利于建立算法模型。典型的地面气液两相流流量计的布置方法有水平布置和垂直布置。垂直布置时，需在设备上游一定距离使用盲三通来混合油气水三相流流体，这样可以避免重力引起的相分布不均。因为初速度的影响，在伽马射线穿过的位置，流体有可能产生偏移，亦即会造成轴不对称，导致计算较为复杂。水平位置放置时，流体可经过较长时间的发展，存在重力引起的相分布不均，但管道很可能是轴对称的。为提高计算速度，获得较快速的算法模型，先用CFD模拟试验的方法，对比了这2种布置方式下，管道截面的相分分布，竖直和水平2种布置方式如图2所示。

图2 伽马阵列气液两相流流量计摆放方式

模拟用文丘里外径D为66 mm，内径d为33 mm，β值为0.5，设定截面含气率(GVF, Gas Volume Fraction)为60%。文丘里前端有10D距离的直管段，以保证流体充分发展。所用模拟软件为Ansys旗下的CFX，计算模型采用均相模型。图3为2种布置方式下文丘里前方1D位置处相分布模拟结果。

图3 竖直和水平布置方式下管道内相分布

由图3可见，模拟结果和预测大致相同，水平放置由于重力作用使管道内相分布相对于竖直方向轴对称，与竖直布置对比具有更好的对称性，这种特性非常利于算法建立以及根据相含率重建截面含气率图像，因此选用水平布置方式更佳。

2.2 γ射线发射器位置分析

由于截面含气率成像算法需要求解像素位置含气率，当以360°等分发射的情况下，每个像素位置显然有非常多的交叉线。理想情况下交叉线越多分辨率越高，通过算法重建的截面含气率图像精度越高，但过多的交叉线对于计算过程来说会非常复杂，因此应适当简化。通过数值模拟分布式布局情况下可以探测到的GVF信号，来分析每个角度布局所具有代表性以及对成像的贡献度。以竖直方向为0°，射线发射器布局位置分别为0、60、90、120、180、225、240、315°，接收器的布局为360°，每隔5°位置设置一个接收点，仍假设工况GVF为60%，设备水平放置，然后获取每个接收位置的信号(等于该点与发射位置连线的GVF)，则各角度位置所获取的信号如图4所示。

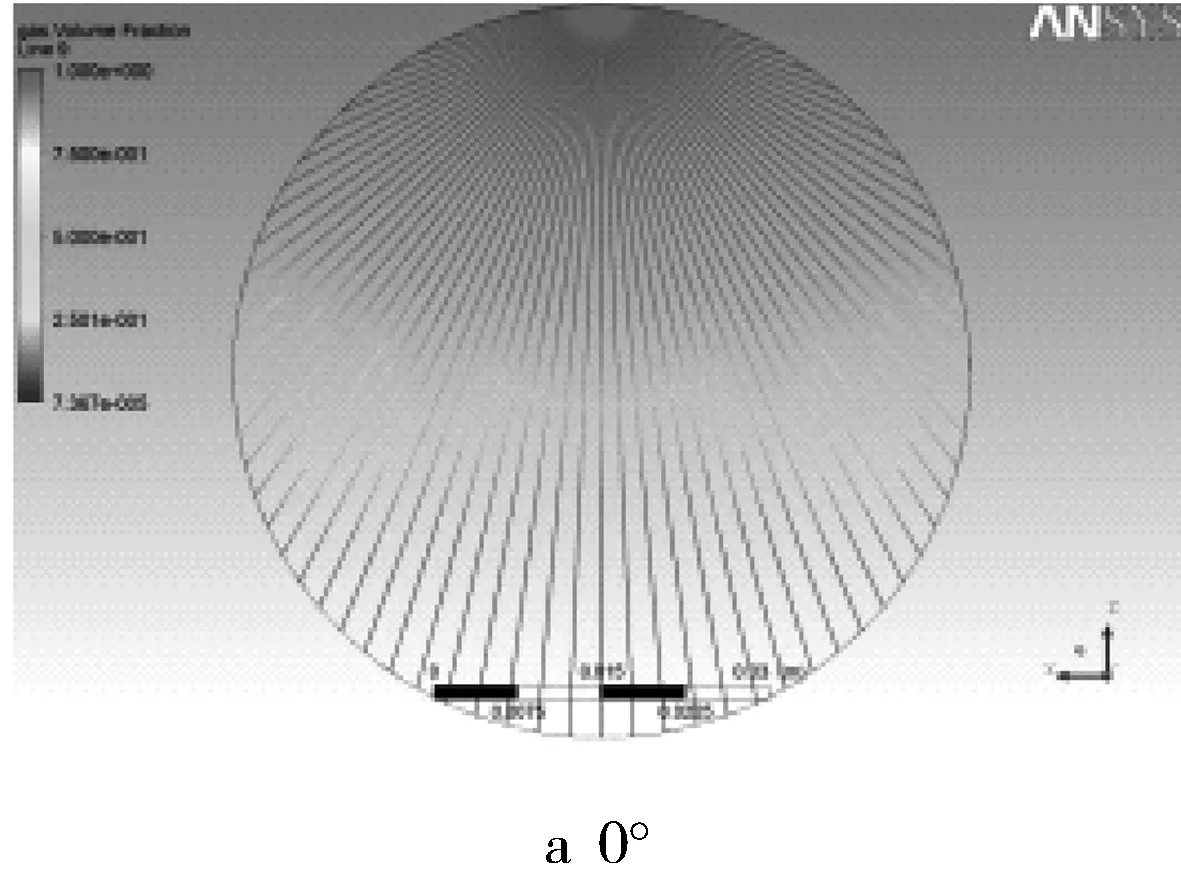
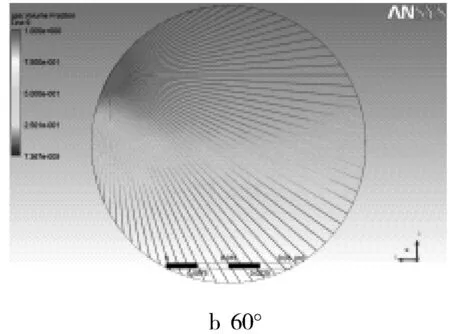
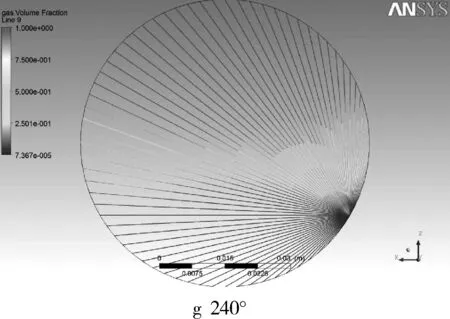
图4 发射器不同角度布局下接收信号效果

由图4可见，各角度的接收信号具有较好的规律性，主要是两侧为GVF等于100%，而中间GVF较低。实际分布中，顶部是GVF等于100%，即全气状态，底部是GVF等于0，即全液状态；可见模拟结果和实际情况比较符合。

虽然每个位置的接收信号有所区别，但总体来说有较好的对称性，且中心GVF较小，顶部较高，这种有规律的图像比较适合建立算法模型。为研究发射器布置的位置，需先研究是否具有对称性，不能在完全轴对称的地方布置发射器，这样建立的方程是无效的。若具有对称性，则发射器可减半。经分析发现，图4d(120°发射器布局)和图4g(240°的发射器布局)所接收到的信号完全对称。

3 伽马阵列成像算法模型

在模拟试验中，讨论了各角度的模拟试验结果，得出了水平气液两相流流量计的轴对称性，各位置的接收结果等。根据这些结果以及阵列成像表面的像素情况，可选择合适的发射位置，来获取阵列成像。仍以GVF为60%的工况为例，当选择2个发射器时，例如0°和90°的两发射器，选择每隔5°设置1个接收器，则获得的射线如图5a所示；选择0°，60°和240°的3个发射器获得的射线图如图5b所示。

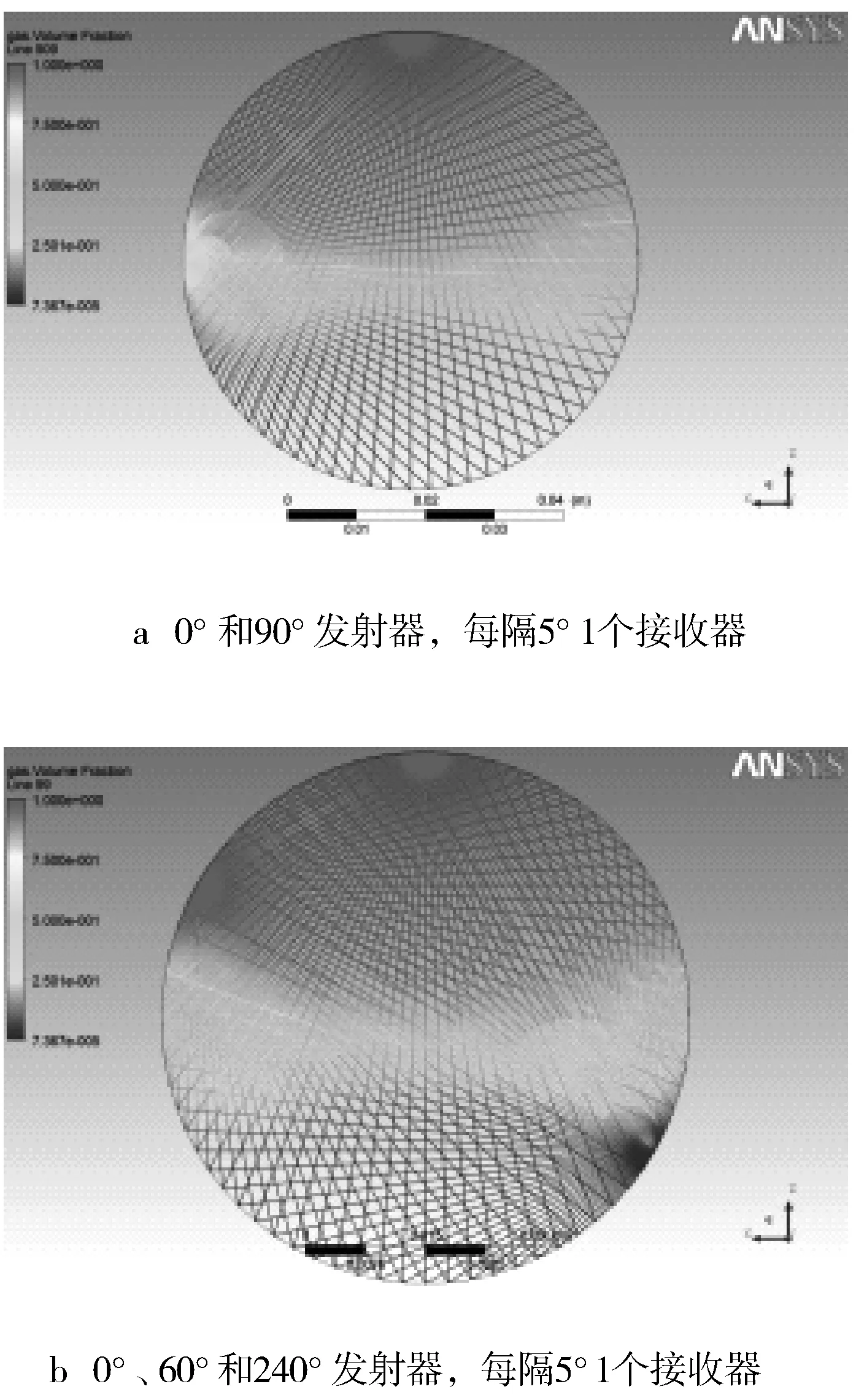
图5 2个发射器和3个发射器布局下成像界面射线分布

由图5可见，选择合适的发射位置，截面射线分布图可以较为均匀，增加发射器，可使截面的射线更多，即可提高像素。截面上发射线的交点分布较为均匀，显然，如果能够求解获得这些交点的GVF，则可利用这些点直接成像。然而，想直接利用这些发射线的GVF数值，来求解截面上所有交点的GVF数值，是非常困难的。因为射线只有144(2×72)条，而交点数远超于此。即使加上方程限定，如顶部为GVF等于100%、底部为GVF等于0这种限定，也不可能解出如此多的点，因此需要降低分辨率。当升级到0°、60°和240° 3个发射器的交叉图谱，则存在216(3×72)个射线结果，这相当于15×15的分辨率(由于是圆形图像，图像的边缘点不参与分辨率求解，因此求解的分辨率能达到15×15)。

以此类推，当需要的分辨率越高，则需要越多的发射器来获得足够的分辨率。每增加1个发射器，可获得72个方程，可根据工程需求，来决定需要多少发射器。例如，当需要获得平面上分辨率为30×30时，则需要约13个发射器。

实际的射线交点，显然比分辨率所需求解的结果要多，每根发射线，最多可以与整个半圆的发射线相交，这将有36个射线交点。最少只与两个发射线相交，平均每个发射线有近20个射线交点，则2个交叉图谱会存在约2 800个交点(20×72×2)。然而纯粹的方程却只能有72个求解结果，因此交点之间必须有一定的数学简化。

根据水平管气液两相流流量计的截面图形样式，可发现：第1是图形呈现顶部GVF等于100%，而底部GVF较低的分布；第2是截面之间的过渡较为均匀。因此，可进行数学简化，第一，求解矩阵可从设置的顶点GVF等于100%开始；第二，像素点不是孤立的，可将截面划分为合理的像素点，然后该像素点范围内的发射器交点，可认为均为同一的GVF。亦即，将截面按成像像素要求，划分为多个像素区，例如，当需要成像12×12的分辨率时，则可直接将截面划分为这么多成像区域，如图6a所示。每个落入该成像区域的点，则近似GVF为该像素区的值。

以0°和90°相交的图谱为例，落在P11-3内的交点有5个，分别是0°和90°发射至320°、325°两条曲线的3个交点和2个边缘点，如图6b所示。此时，由于像素相等，可直接认定这5个点GVF相同，亦即同一个像素区间内的GVF相等。增加了该条件，则可达到方程和分辨率之间的统一，即所给的GVF射线方程和分辨像素可求解。

以0°和90°角的交叉图谱为例，按数学理论，不考虑方程限定，可以认为，144个射线结果只能解出144个点，也就是说，这只相当于12×12的分辨率。显然，该分辨率有点低。

图6 成像算法像素范例

更进一步，由于所给的像素区长度及大小相同，则射线的值，可直接近似变成射线经过的路径上的所有像素点的总和。以图6b为例，则90°发射到320°角度的射线经过了P1-6，P2-6，P3-6，P4-6，P4-5，P5-5，P6-5，P7-5，P7-4，P8-4，P9-4，P10-4，P10-3，P11-3。其中P后面的第1个数值代表自左到右的格数，第2个数值代表自上到下的格数。需要注意的是，由于射线在有些横格数上会经过2个竖直格数，例如P4格，P7和P10格，他们均经过5到6格，4到5格和3到4格两个格数，由于横格长度相同，因此最终的简化方程可变为：

GVF(90-320)=[P1-6+P2-6+P3-6+(P4-6+P4-5)/2+P5-5+P6-5+(P7-5+P7-4)/2+P8-4+P9-4+(P10-4+P10-3)/2+P11-3]/11

以此类推，可建立所有像素点和发射线之间的关系。

需要注意的是，像素点和射线并非一一对应，导致方程可能存在明显的超定现象。因此，计算时，需要考虑迭代计算，以最小二乘法，多元线性回归，使计算的误差最小，此时，这些像素点的值可被近似求解。最终将这些像素值充满方块，获得表面图像。

求解过程中，可从顶部开始，因为在气液两相流状态下，P6-1和P7-1点的GVF等于100%。然后，按逆时针方向，开始逐条射线求解。

4 结论

1) 经过CFD数值模拟，分析了水下流量计截面含气率成像的可行性，通过对模拟结果的讨论，证明了水平测量管道布置方式更有利于成像测量；射线发射器的布置需要错开完全对称的角度，以避免引入无效方程。

2) 提出的成像算法在保证较高分辨率的前提下，进行适当简化以加速求解过程，对水下流量计截面含气率成像技术提供理论依据。