油套管特殊螺纹密封面微观泄漏机制研究*
2019-08-27颖1练章华谧1林铁军
张 颖1 练章华 周 谧1 林铁军
(1.四川轻化工大学机械工程学院 四川自贡 643000;2.西南石油大学油气藏地质及开发工程国家重点实验室 四川成都 610500)
随着我国天然气勘探开发的不断深入和井下工作环境的日趋复杂,具有较高气密封性能的特殊螺纹接头广泛应用于高温高压气井。目前全世界已开发出100多种享有专利技术的特殊螺纹接头,但普遍使用的只有德、美、日等少数国家的10余种产品[1-2]。我国在油、套管螺纹密封和强度设计、制造、产品信誉、创新专利以及相关基础理论研究等方面,与国外相比还存在一定差距。国外著名公司持续改进或推出管端新结构特殊螺纹接头[3-5],但是几乎不公布其依托或支撑的机制或设计理论。国内油、套管特殊螺纹接头的研发,基本基于反复的加工和实验室评价,对管端特殊螺纹接头机械密封的设计和气体泄漏机制缺乏基础性研究。
目前,国内外大多数特殊螺纹接头密封性能的研究,主要通过有限元和试验的方法,在宏观尺度上进行定性或定量描述[6-8]。SUGINO等[9]针对井下恶劣工况环境,研发了高性能的油套管特殊螺纹接头,大量的物理测试以及数值仿真分析结果表明,该螺纹接头可提高密封性能的可靠性。HAMILTON等[10]应用超声波检测的方法获得相互啮合的特殊螺纹密封面之间的接触应力,并详细分析了影响特殊螺纹密封性能的因素。王建东等[11]采用有限元分析的方法研究了不同密封结构形式下,特殊螺纹接头密封能力随载荷的变化规律,并通过实验与数值模拟结果的对比,提出了特殊螺纹接头密封性能判据新的准则。郭建华和马发明[12]开展了油管上卸扣和交变载荷作用下螺纹气密封性室内试验评价。马艳琳等[13]基于密封接触能机制和密封面屈服条件,建立了特殊螺纹气密封性能定性的评价方法,对比分析了密封面平均接触应力和密封接触长度对特殊螺纹密封性能的影响,并绘制了锥面对锥面密封结构的密封包络线,利用密封包络线,可以指导特殊螺纹扣密封结构参数设计。
特殊螺纹金属对金属密封是一个复杂而又难以解决的问题,其密封可靠性不仅与主密封面的结构和油套管材料性能有关,而且与螺纹接头密封面表面粗糙度、泄漏介质特性等因素有关。本文作者从微观尺度上揭示特殊螺纹金属对金属密封的泄漏机制,建立微观尺度下特殊螺纹接头主密封面金属对金属密封气体泄漏的数学模型,并在此基础上建立气体通过特殊螺纹金属对金属主密封面的泄漏率理论模型,分析密封面平均接触压力、密封面粗糙度、密封面有效长度对气体泄漏率的影响规律。
1 金属密封微观泄漏机制
特殊螺纹主密封面粗糙度是影响气密封泄漏率的一个重要参数,但是由表面粗糙度引起的泄漏机制并没有深入的研究。实际上,所有的宏观尺寸下的物体都存在表面不均匀现象。当两个平板物体相互接触时,在微观尺度上,有效接触区域在接触范围内随机分布,并且有效接触区域面积占整个接触区的比例较小。绝大多数的工程材料表面都有自己的加工精度,即表面粗糙度,并且该表面加工精度将会极大地影响密封泄漏速率。图1所示为微观尺度下,特殊螺纹主密封面的接触情况[14-15]。图中,黑色区域代表特殊螺纹密封触表面的有效接触区域,白色区域代表了密封接触表面的无效接触区域。这是由于特殊螺纹主密封面粗糙度引起的密封表面不完全接触现象。从图中可以明显看出,气体可以轻易地沿着无效接触区域渗透。这就从微观上揭示了特殊螺纹金属密封气体泄漏机制。

图1 特殊螺纹主密封面微观泄漏机制
图1所示是微观尺度下的金属接触密封泄漏简图,为了便于统计计算,可以将其等效为一个相同尺度下的方格图,如图2所示。图中接触区域表面长度为l,方格边长为λ。表面接触区域内的放大倍数ξ可以定义为
(1)
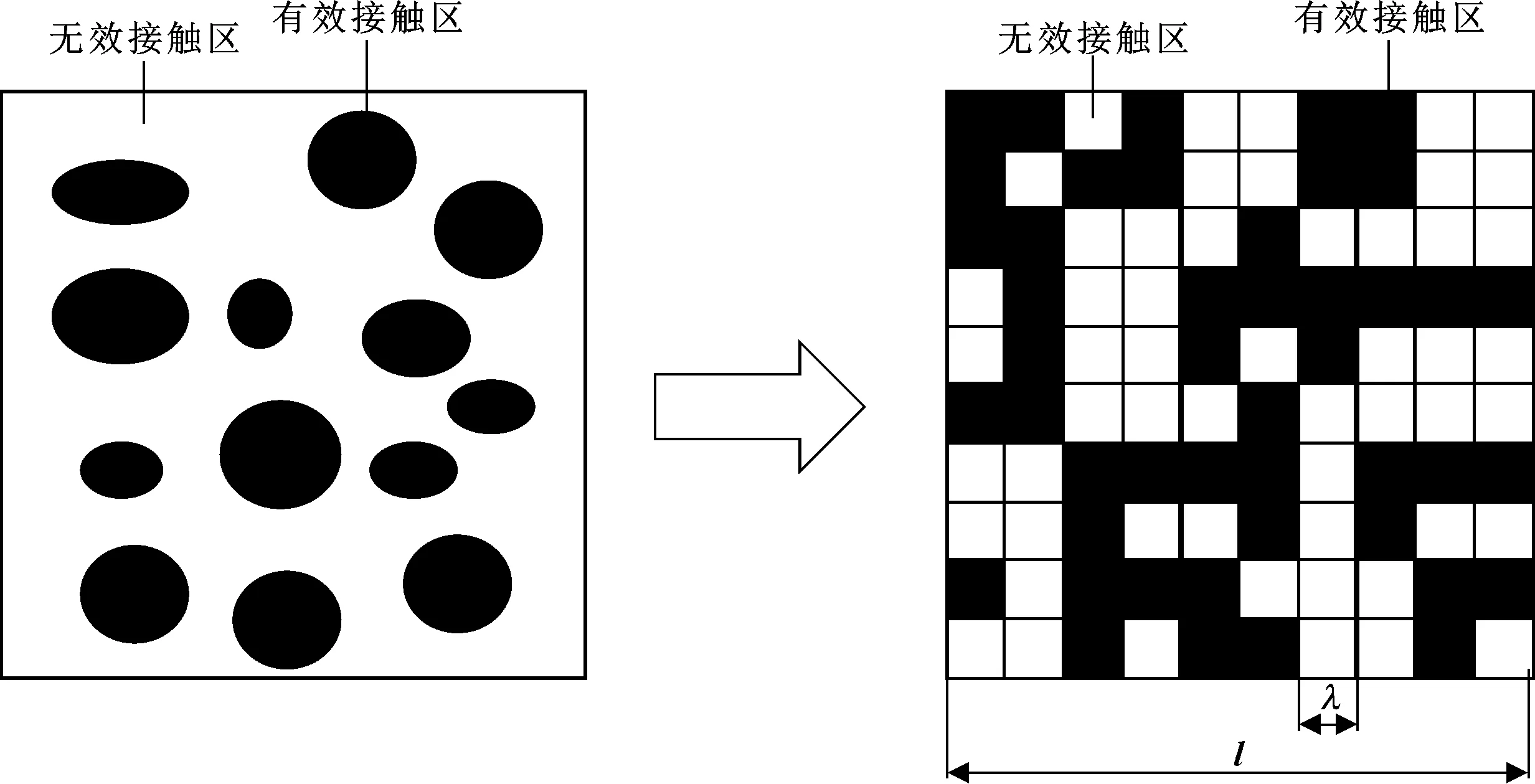
图2 微观泄漏接触面接触区域等效图
为了描述密封界面的空隙分布状况,将密封界面划分为网络矩阵形式,随着放大倍数的增加,密封界面间的非接触区域随之变多,当放大倍数达到某一临界值时,便会出现一条网络单元(称之为泄漏通道),将密封界面未接触的两部分连接起来,如图3所示。可以看出,放大倍数可以直接地影响到有效接触区域的面积。在宏观接触区域范围内,随着放大倍数的增加,有效接触区域面积也在相应地减小。

图3 接触表面在不同放大倍数下的有效接触面积
同理,当在宏观尺度下(ξ=1)研究表面粗糙度对气体泄漏率的影响,在接触压力作用下,整个接触区域面积内填满黑色方块。当增大放大倍数ζ时,此时由于表面粗糙度影响,即表面不平整现象,接触区域内将会出现白色方块,即无效接触区域,该区域内的接触压力为0。当放大倍数上升至某一临界值ξc时,此时在名义接触区域内将会出现一条泄漏路径,如图3(d)中箭头所示。此时的无效接触区域将成为螺纹密封面之间的泄漏通道。泄漏的概率用P(ξc)表示,其表达式为
(2)
式中:ξc为临界泄漏放大倍数;A(ξc)为临界泄漏放大倍数下的无效接触面积;A0为名义接触面积。
2 特殊螺纹微观泄漏模型
假设特殊螺纹扣密封面采用锥面对锥面的主密封形式,在微观尺度下,密封面形式可以视为两个平行板相互接触,如图4所示。通过密封面气体渗透模型可以推导气体泄漏量的数学表达式。
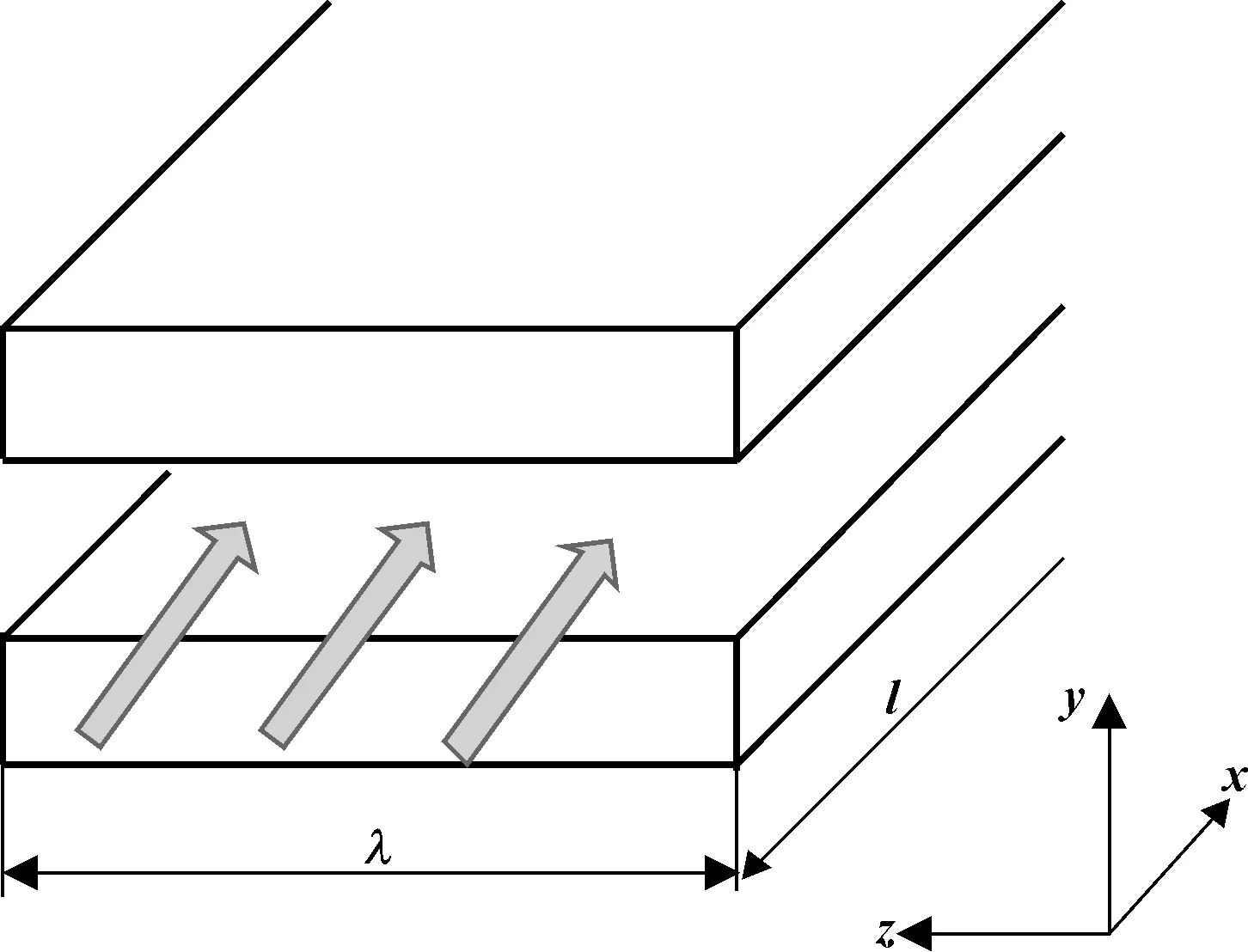
图4 特殊螺纹密封面气体渗透平板模型
在图4中,假设气体的泄漏通道是沿着x方向进行,那么气体在x、y、z方向的流速分别为
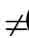
(3)
(4)
Navier-Stokes方程为
(5)
将式(3)代入式(5),则有:
(6)
将式(4)代入式(6),则有:
(7)
因此式(7)可以写为
(8)
对式(8)进行积分求解,可得
(9)
其边界条件为: 当y=0或者y=h时,u=0。其中h为两个平行板之间的间隙,可以得到:
(10)
将式(10)代入式(9),可以得到气体流速的表达式:
(11)
根据气体流速方程可以得到密封面之间的泄漏量,其泄漏流速Q的积分表达式为

(12)
将气体流速表达式(11)代入气体泄漏流量方程式(12),则有:
(13)
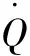
假设螺纹密封面间,气流泄漏流道有N块方白板,如图3(d)所示。那么螺纹密封面泄漏速率的表达式为
(14)
从式(14)可以看出,气体泄漏体积速率与油管内外部压差呈正比,并且与接触面之间的间隙h和临界泄漏通道边长有关,而h和直接反映了密封面的光洁度或粗糙度。密封面越粗糙,h和越大,那么气体泄漏速率也就越大。值得注意的是,泄漏通道方块数N的取值与临界放大倍数有关,当接触面积一定时,泄漏方块数N越大,那么临界放大倍数越大。
而接触面间隙h(ξ)的表达式[16]可以写为
(15)
其中,
(16)
式中:E为油管材料的弹性模量;p0为主密封面的密封接触压力;C(q)为油管材料表面粗糙度能量谱;q0、q1为分别为最小截止频率和最大截止频率;A0和A(ξ)分别为名义接触面积和真实接触面积;p0和p(ξ)分别为名义接触应力和真实接触应力。
3 特殊螺纹主密封泄漏影响因素分析
特殊螺纹接头密封的可靠性即取决于主密封面的结构设计,还与深井、超深井油管工作环境和使用条件有关。一般而言,影响油管特殊螺纹密封性能的主要因素有:高温高压下天然气的物理性质;接头螺纹密封面表面粗糙度;螺纹主密封面之间的接触压力;油管接头材料的力学性质以及使用工况条件等。文中利用所建立的特殊螺纹密封面接触压力模型和气体泄漏模型,分析特殊螺纹主密封面在不同设计参数和工况条件下气密封性能。
假设油管接头密封气体压差为70 MPa,采用114 mm油管,油管材料的弹性模量为2.06×105MPa,螺纹密封面接触接触长度为6 mm,密封面粗糙度为1.2 μm,表面分形维数取1.36。假设特殊螺纹主密封面分形维数Df=2.2,其特征频率为qL=104m-1,最低截止频率q0=105m-1,最高截止频率q1=1010m-1,表面高度均方根hrms=10 nm。
3.1 密封面接触应力对泄漏率的影响
图5所示为气体密封泄漏量与密封面上平均接触压力的变化曲线。可以看出:随着螺纹密封面平均接触压力的增加,气体泄漏率开始时逐渐减小,最后逐渐趋于平稳;当密封面上接触压力大于640 MPa后,每15 min气体泄漏量小于0.02 cm3。总体上看,应该尽量提高密封面的平均接触应力,减小密封面未接触区域的微小间隙,增大气体的流动阻力,从而减小密封气体的泄漏体积。
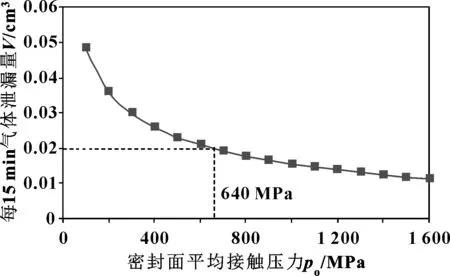
图5 密封面平均接触应力对气体泄漏率的影响
3.2 密封面粗糙度对泄漏率的影响
根据文献[17]可知,当表面粗糙度Ra在0.11.6 μm时,分形维数Df和粗糙度呈近似线性关系且:
Df=1.78-0.35Ra
(17)
气体泄漏率随密封面表面粗糙度的变化关系如图6所示。可以看出:随着密封面表面粗糙度的增加,气体泄漏率呈幂指数规律增加,且密封面平均接触压力越低,气体泄漏率受表面粗糙度的影响程度也就越大;当密封面粗糙度小于0.8 μm时,3种接触压力下的气体泄漏率几乎相等,而当密封面粗糙度大于1.6 μm时,3种接触压力下的气体泄漏率差距明显,且接触压力越低,气体泄漏率越高。这是因为当密封面粗糙度较低时,接触面较光滑,即使在较低的接触压力作用下,密封面的有效密封接触区域也比较大,密封面之间间隙较小,从而使得气体的泄漏路径减小,流动阻力增大,气体泄漏率较低;而当密封面粗糙度较大时,随着密封面上平均接触压力增大,密封面的泄漏通道将被塑形流动填充,从而增大有效密封面积,减小密封面之间的间隙,因此气体泄漏率也就越来越低。总体上看,如果要求密封每15 min泄漏量小于0.02 cm3,在平均接触应力分别为350、500和650 MPa 3种应力状态下,密封面表面允许的最大粗糙度依次为1.1、1.2和1.32 μm。
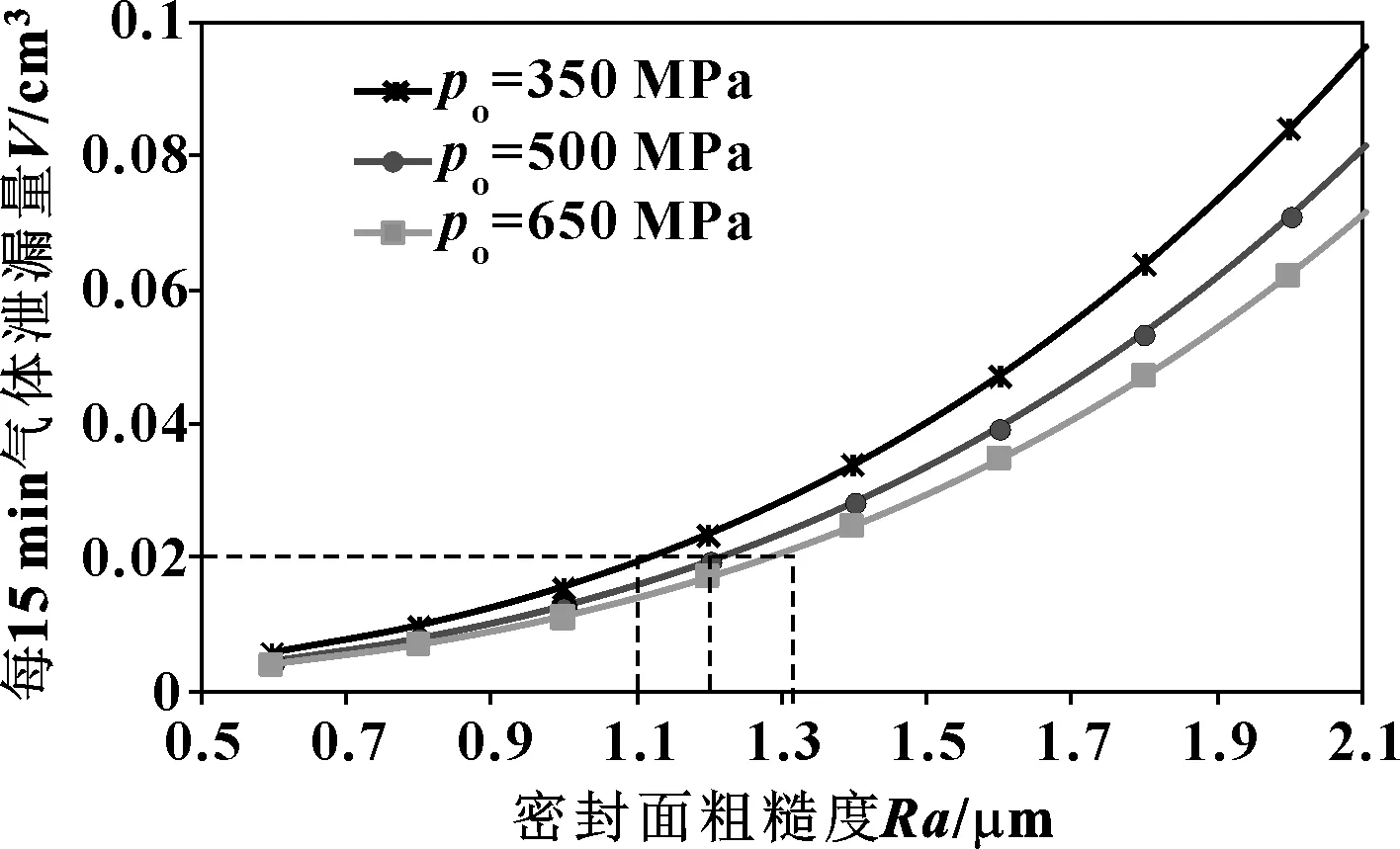
图6 密封面粗糙度对气体泄漏率的影响
3.3 密封面有效长度对泄漏率的影响
根据气体微观泄漏理论模型,分别计算了密封面接触压力为400、600和800 MPa情况下,密封面有效长度为1~16 mm时的气体泄漏率,如图7所示。
从图7可以看出,随着特殊螺纹接头密封面有效接触长度的增加,气体泄漏率逐渐减小,当密封面有效接触长度小于6 mm时,气体泄漏速率下降很快,此时密封面有效接触长度对螺纹密封气体泄漏速率影响较为明显;而当密封面有效接触长度大于9 mm时,气体泄漏速率下降较为平缓,说明此时密封面有效接触长度对螺纹密封气体泄漏速率的影响不明显。同时从图中还可以看出,螺纹密封面平均接触应力越低,密封面有效接触长度对气体泄漏速率影响越显著。总体上看,如果要求气体密封每15 min泄漏量小于0.02 cm3,在密封面平均接触应力为400、600和800 MPa 3种应力状态下,密封面所需要的最小有效接触长度依次为8.2、6.3和5 mm。
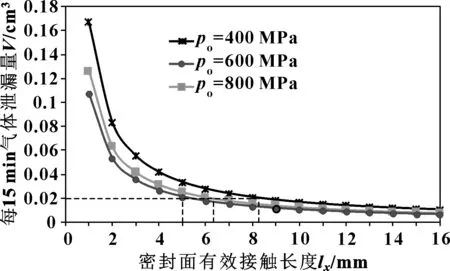
图7 密封面有效长度与气体泄漏率的关系
4 结论
(1)根据特殊螺纹接头金属对金属密封原理,从微观尺度下揭示了特殊螺纹接头的气密封泄漏机制,并建立了微观尺度下特殊螺纹气密封泄漏的力学数学模型。
(2)考虑特殊螺纹密封表面粗糙度下,建立了特殊螺纹主密封面气体泄漏率的数学模型,并详细分析了影响特殊螺纹气密封性能的主要参数,包括密封面上的接触应力、密封面的粗糙度以及密封面的有效接触长度。
(3)根据特殊螺纹气体泄漏数学模型,计算分析了特殊螺纹气密封性能影响规律,结果表明:随密封面接触应力的增大,气体泄漏率呈幂率指数规律降低;随密封面粗糙度的增加,气体泄漏率随之增大;随密封面有效接触长度的增加,气体泄漏率呈幂率指数规律降低。
