精选问题引出新知，明辨重点突破难点——以二次函数单元起始课为例

☉江苏省海门市首开东洲初级中学 夏冬平

二次函数的起始课是很多教研活动的热点课题，常常成为同课异构的课题.最近我们备课组也进行了这节课的集体备课，大家经过充分研讨，结合一些参考文献中的课例设计，确认了从具体问题中分析出二次函数关系，并安排学生类比一次函数定义二次函数，然后尽快进入二次函数图像和性质的探究，把本课的教学重点与难点定位在函数图像的生成及性质的归纳上，经过教学实践，取得了较好的效果.本文梳理该课教学流程，并给出教学立意的解读，供研讨.

一、二次函数单元起始课教学流程

活动1：分析具体问题中的函数关系

问题1：正方体的六个面是全等的正方形（如图1），设正方体的棱长为x，那么正方体的表面积y与x之间有什么关系？

图1

问题2：设n个球队参加比赛，每两队之间进行一场比赛，比赛的场次数m与球队数n有什么关系？

问题3：某种产品现在的年产量是20t，计划今后两年增加产量.如果每年上一年的产量增加x倍，那么两年后这种产品的产量y将随计划所定的x的值而确定，y与x之间的关系应怎样表示？

问题1：y=6x2.

问题2：）.

问题3：y=20（1+x）2.

归纳：上面的问题中，函数都是用自变量的二次式表示的.一般地，形如y=ax2＋bx＋c（a、b、c是常数，a≠0）的函数，叫作二次函数.其中x是自变量，a、b、c分别是函数解析式的二次项系数、一次项系数和常数项.

预设追问：上面三个表达式都符合二次函数的一般形式吗？如果不是，请整理成一般形式，并指出二次项系数、一次项系数和常数项.

跟进练习：如图2，矩形绿地的长、宽分别为30m、20m，现各增加xm，写出扩充后的大矩形绿地的面积y与x的函数关系式，并指出各项系数.

预设：y=（30+x）（20+x），即y=x2+50x+600.它的二次项系数是1，一次项系数是50，常数项是600.

过渡：回顾一次函数的学习经验，大家觉得接下来会如何研究二次函数？

预设：学生先独立思考，再在小组内交流，并构思一下如何研究，还可形成研究路径，再挑选学生进行全班展示交流.师生互助引出从特殊出发进行研究，引向下一个学习活动.

活动2：研究二次函数y=x2的图像和性质

独立思考：如何研究y=x2的图像和性质？

小组讨论：根据学习一次函数图像和性质的经验，对一个函数要研究什么？怎样进行研究？

预设：在学生回答的基础上，引导学生不要急于进行列表、描点、连线，而要先认真观察函数解析式的特点，想清自变量的取值范围，函数值有怎样的特点，构思怎样列表、取点更有代表性，以避免在选点的“试探”过程中有盲目性.经过启发，让学生按以下流程进行研究，比如，先从解析式进行研究，再选择恰当的数进行计算后列表分析，观察表格中有序数对的特征，猜想函数图像的大致特点，最后才是描点验证之前的观察和猜想.具体如下：

第一步，观察解析式，确认自变量x的取值范围是全体实数，函数y≥0，可以猜想这个二次函数图像有什么特征.

第二步，列出表格，同学们交流分享刚刚观察解析式得出的结论，对照列表后看是否分析出的结论仍然成立.

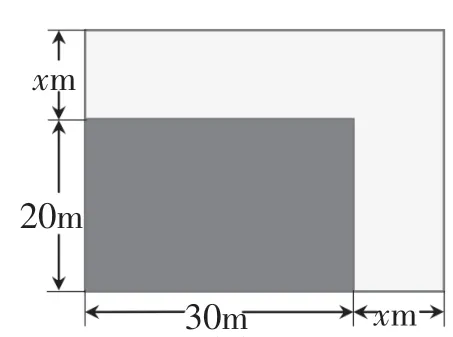
图2

表1

并预设追问：表格中的点关于y轴对称，这个性质能从解析式中看出来吗？

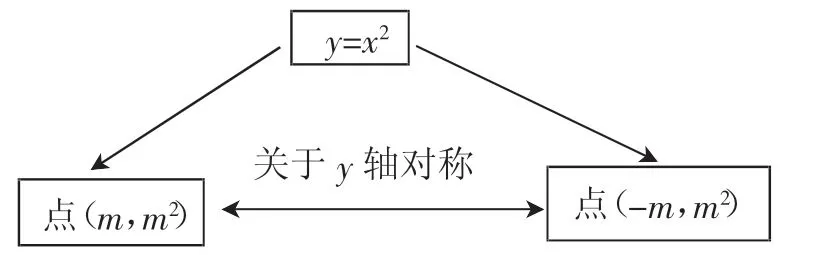
图3

从表格中还能获取什么信息？（预设增减性，当自变量取正数时，函数值随着自变量的增大而增大；当自变量取负数时，函数值随着自变量的增大而减小）预设表格图示标注信息如下（注意根据学生课堂生成渐次呈现）：

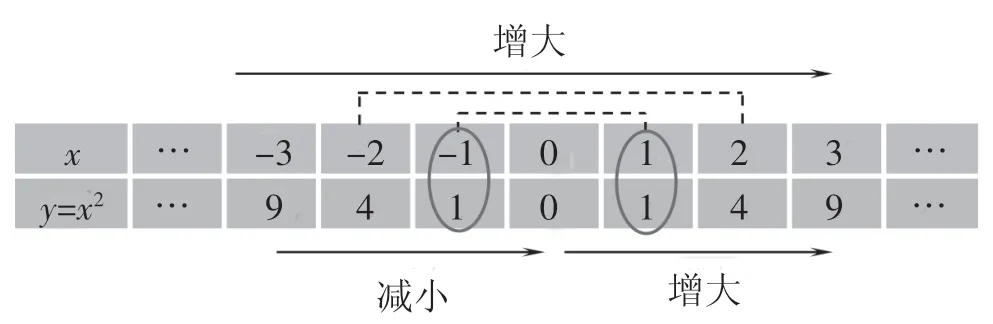
图4

（3）从函数图像看：上述信息，我们再通过描点、连线、画图像来体会并验证一下.

表2

师生共同小结函数y=x2的性质.这个表格中的一些研究“元素”也可以适当留白，让学生参与构建，以便对研究二次函数图像的一些角度有较深的认识.

活动3：类比函数y=x2，分组研究函数y=-x2、y=2x2、y=-2x2的图像和性质

教学组织：学生分组研究函数y=-x2、y=2x2、y=-2x2的图像与性质，教师在巡视过程中分组指导，参与研究活动，最后引导学生展示他们的成果.在此基础上，安排学生猜想、概括函数y=ax2（a≠0）的图像与性质.

预设：学生的回答如果比较零乱，教师可启发学生结合前面使用表格归纳的一些经验，列表梳理归纳二次函数y=ax2（a≠0）的图像与性质，如|a|的大小对抛物线开口大小的影响；最后将二次函数y=ax2（a≠0）的图像特征与函数性质，在师生合作后梳理出表格（限于篇幅，略去）.

活动4：课堂小结，研究展望

小结问题1：这节课我们是研究二次函数，你学习了二次函数的哪些内容？

小结问题2：在研究二次函数的图像与性质的过程中，你觉得哪几条重要经验值得与大家分享？

小结问题3：根据以前学习一次函数的经验，你觉得教材编写者在二次函数这一章会有怎样的学习目录？请帮助拟一下，在小组内分享交流.

二、教学立意的进一步阐释

1.精选问题情境，引导学生抽象并概括二次函数的定义

数学来源于生活，初中阶段几种初等函数作为一种重要的数学模型也是从实际问题中抽象出来的，不同版本的教材都设计了一些生活情境用来引导学生列出二次函数关系式，从而定义二次函数，我们也采用了教材上的典型问题情境，但是进行了问题呈现顺序的重组，并且安排学生课前自主先学，节约课堂时间，这样开课阶段小组直接汇报所列的关系式，从而发现它们共同的特征，从变量与变量之间的对应关系确认是二次函数关系，很自然地引出课题：二次函数，进一步通过类比定义一元二次方程的一般形式.由于这块内容并不是本课重点，对学生也不构成挑战，所以我们尽快推进到下一教学环节，研究二次函数的图像及性质.

2.明辨教学难点，把教学用力点放在函数图像生成上

本课的教学重点是二次函数的图像和性质，难点是得出图像并归纳性质.与一次函数学习的经验类似，我们也是组织学生从简单出发，先研究函数y=x2的图像，由解析式能看出x可以取任意实数，不妨以0为“基准”，向左、右均匀选便于计算的x的值，先想象画出来的图形的大致形状，然后列表、描点.之所以让学生认真观察解析式、观察表格中数对的特征，就是因为最初接触一个陌生函数的未知图像时，选值列表往往带有一定的试探性，为了避免盲目性，要先想后画，争取所画出的图像比较接近精准的图像.当然，由自变量取值范围看，只能画出部分图像.由选点的个数、描点的近似等因素，决定画出的图像是近似的.在修正或优化函数y=x2的图像时，可以建议学生把原点附近的部分再画细一些.采取“加密”的方法，在-1与1之间，每隔0.2取一个x的值，列表、描点、连线，就得到原点附近部分相对精确的抛物线了.

3.预设小结问题，引导学生回顾所学并展望后续内容

从上面的课例来看，本课的几个小结问题也是我们精心预设的，主要立意有三点：首先，引导学生回顾本课所学知识；其次，在学习研究函数图像过程中，将积累的一些经验、关键步骤通过反思环节小结出来；三是向学生传递函数研究的套路，比如我们是通过具体实例认识这类函数，接着要研究这类函数的图像和性质，展望后续，还将探究这类函数与相应方程的联系，并利用这类函数解决一些实际问题.