“集慧式”教研，有效突破教学难点——以“无理数的小数部分”为例

☉江苏省苏州工业园区青剑湖学校 赵晓黎

一、提出教研话题

下课之后，笔者想起本地区一个青年教师教学研讨群，于是提出如下的教研话题：

二、“探究无理数的小数部分”教学微设计展示

问题提出之后，群里不少教师积极参与，除了几个教师从解法的角度进行研讨，不少教师还给出精彩的教学微设计及打磨意见，下面梳理出比较典型的两种.

教学微设计（一） 探究无理数的小数部分

活动1：填表1并分析.

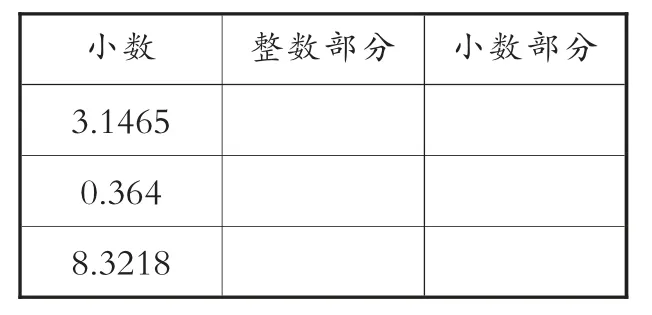
表1

小数=______+______；

小数部分=___________.

活动2：分析无理数的整数部分与小数部分.

（1）求a的整数部分；

（2）求a的小数部分.

讲解预设：（1）因为4＜7＜9，所以，所以2＜，所以的整数部分为2.

活动3：变式练习.

简评：用两个活动递进式安排，活动1作为活动2的铺垫，较好地化解了难点，应该有较好的教学效果；活动2也是先引导学生分析整数部分，再分析小数部分，层层推进，逻辑性强；活动3跟进变式练习，有很好的教学操作性.

教学微设计（二） 探究无理数的小数部分

问题1：写出无理数的整数部分.

预设：因为4＜7＜9，所以，所以＜3，所以的整数部分为2.

追问：写出的小数部分.

预设：的小数部分为的小数部分为.并引导学生小结“一个无理数的小数部分就是用无理数减去它的整数部分”.

问题2：写出的整数部分、小数部分.

预设：，根据不等式的性质，＜3+5，即，所以的整数部分为7，小数部分是，即.

同类练习：写出的整数部分和小数部分.

问题3：写出的整数部分、小数部分.

预设：因为，根据不等式的性质＜-2，进一步，即的整数部分为2，小数部分为.

同类练习：设的整数部分为a，小数部分为b，求a-b的值.

变式研究：写出的小数部分.

预设：根据开立方运算与立方运算的互逆关系，可分析出，于是的整数部分为2，则它的小数部分为.

变式再练：若的整数部分为a，的整数部分为b，求a-b的值.

拓展提升：分析的整数部分.

预设：先将平方得11+，再分析出，所以，所以16＜21＜11+，所以，所以的整数部分为4.

简评：这是一份精彩的微专题教学设计，由浅及深，变式生长，对难点的突破能从不同角度入手，特别是问题2、问题3能联系到不等式性质来解释无理数的整数部分，对于攻克解题或教学的难点有很好的效果，而且能让不同的学生有不同的提升，这是这个教学设计活动的亮点！作为一节微专题讲评课，是一份优秀的设计，可以直接印发学案让学生练习后再讲评.

改进建议：考虑到数轴是重要的数形结合的工具，可以借助数轴来研究无理数的整数部分和小数部分.结合两点之间距离公式，下面我们形象地揭示的小数部分，因为想清的小数部分后，仍然可以借助数轴进行研究、直观分析.

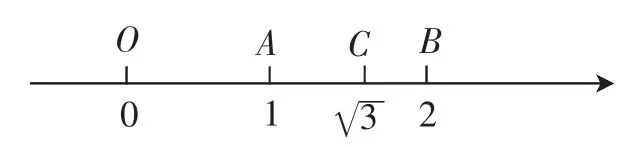
解读：在数轴上表示出所对应的点C，直观地看出线段AC的长对应着的小数部分.

这种在数轴上研究的思路，也可迁移到另外的问题中，可以使本课教学从数、形两个角度带领学生去思考、对比.让学生从“形”的角度来理解，也体会到数形结合，以及数轴的强大功能.

三、关于网络微研的进一步思考

1.发挥网络微研优势，开展“集慧式”教学研讨

这次成功的网络微研活动启发笔者重视开展网络微研，创造条件开展“集慧式”教学研讨活动.相对于目前一些规模学校“一周一次”集体备课而言，注重用好微信群、QQ群，可随时开展网络研讨，教师课余都可关注一下感兴趣的教研群中一些教研话题，自由发表自己的教研意见或教学设计，避免了在一个学校的备课组中大家“端正坐着”听几个经验丰富的老教师“一直在说”，年轻教师往往只有“听的份”.

2.提出微型研讨话题，激发青年教师的参与兴趣

为了有效调动青年教师参与网络教研话题，选择的教研话题应尽可能“微小”，具体来说，不宜提一些宏大的教研话题，比如，怎样命制一份期中试卷？课堂上怎样开展追问？数学教师怎么研读教材？如何开展省级课题研究？等等.这类宏大的不着边际的网络教研话题，往往得不到青年教师的关注，即使偶有“回复”，也是无甚价值的交流研讨.像本文这样，从一道具体的习题出发，基于多数学生解答有困难的教学现状，促进大家思考如何求解，怎样开展更有效的教学，促进学生更好地理解，就得到了很多青年教师的积极参与，达到了较好的教学微研的效果.

3.研究习题为出发点，让教学微设计成为落脚点

当前，有些微信群、QQ群在研讨交流过程中，过分偏向一些难题的解法探讨，热衷于收集或展示一些技巧性的解法，多数都是超越教材和课标要求的网红题及“神仙下凡式”解法.这类研讨偶尔为之，无可厚非，但不能成为教研常态，对青年教师的专业发展非常不利，因为教师的精力有限，如果把精力过分聚焦在这些网红题、无趣题、超标题上，对教学基本问题缺少长期、深入的关注，则不利于教师专业成长.所以，我们提倡要从研究习题（特别是研究经典习题）出发，让解题研究（解法研究）走向解题教学研究，特别是针对某一道题或其中的关键步骤进行教学微设计的研究，这样坚持下去积累多了，有利于教师沿着“关注教学基本问题”这条康庄大道走向远方.