以学定教，择教推思——“三角形中位线定理证明”的教学实践与思考

☉江苏省宿迁市实验学校 王晓明

“以学定教”的核心是“以学生为主体”，学生现有的知识发展水平、已有经验、思维特征、兴趣爱好是教师用来确定教学内容、过程及方法的依据.“择教推思”的核心是“以教师为主导”，根据学情选择教学内容、过程及方法，教学生学提问、学建构概念、学寻找方法、学研究问题的一般方法，教学生学会思考.

现以“三角形中位线定理证明”的教学为例，就教学实践中以学定教，推动学生数学思维发展，谈谈笔者的做法与思考.

一、基本情况分析

三角形中位线定理是许多有关线段数量和位置关系证明的重要依据.苏科版教材将它安排在八年级下册“中心对称图形——平行四边形”这一章，安排在平行四边形的性质和判定之后.学生已经学过三角形的相关性质和全等三角形的关系，教材将三角形中位线放在平行四边形之后教学，显然是想作为平行四边形研究的自然延伸，但教材不是以平行四边形的问题来发现探索定理，而是安排了将一个三角形剪拼成平行四边形来体现定理的探索过程，这一探索过程从知识的发展角度看略显凸兀.

从数学知识角度来看，三角形中位线定理其实是平行线分线段成比例定理内容的一般化推广和逆向研究的结果.教材将平行线分线段成比例定理安排在九年级下册，作为相似三角形的判定基础.这种分散安排体现了降低难度和够用即可的意图，同时给本课学习体现知识发展过程、合理自然生长带来了困难.

教学目标：探索并证明三角形中位线定理.经历观察、操作、猜想、归纳、验证、反思等活动过程，发展空间观念和有条理的表达能力、数学合情推理和演绎推理的能力.

教学重、难点：探索中位线定理证明的辅助线的添法.

二、教学过程与分析

1.平行四边形分离三角形

活动1：如图1，直线l经过▱ABCD的对角线的交点O，与平行四边形的边分别交于E、F两点，观察直线l绕点O旋转的过程.

发现：始终有OE=OF.如图2，当直线l经过一组对边的中点时，得到四边形BEFC、AEFD均为平行四边形，则EF∥BC∥AD、EF=BC=AD.由于线段EO和FO分别是△ABC和△ADC的一条中位线，且有EO∥BC，FO∥AD，EF=BC=2OE，则EF=AD=2OF.

猜想：三角形中位线平行于第三边，并且等于第三边的一半.

图1

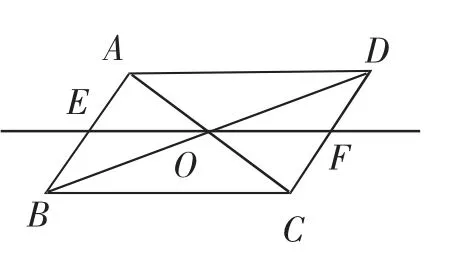
图2

验证：画出图2中的△ABC，如图3，EO为△ABC的中位线.由图2得到启示，要证明EO与BC的数量和位置关系，关键是要构造出▱BCFE.由图2知，OF在EO的延长线上并且等于EO，如果从得到线段OF考虑，可以这样来添加辅助线，进行定理证明.

证法1：如图4，延长EO至点F，使得FO=EO，连接CF.

由EO=OF，AO=OC，∠AOE=∠COF，得△AOE△COF.则AE=CF，∠AEO=∠CFO，则AB∥CF.

由BE=AE，AE=CF，得BE=CF.

由BE∥CF，BE=CF，得四边形BCFE是平行四边形.则EF=2EO=BC，则

如果从得到线段CF考虑，由图2知，CF与BE相等且平行，如果过点C作一条与BE相等的线段，则会有无数条，但如果作与BE平行的线段则有且仅有一条，于是得如下证法.

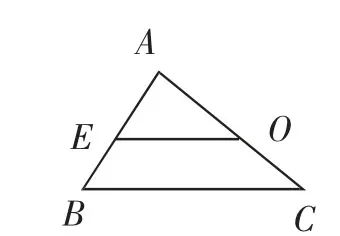
图3

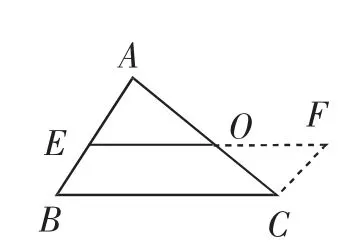
图4

证法2：如图4，过点C作CF∥AB，交EO的延长线于点F.

如果从直接得到△COF考虑，可以旋转△AOE直接得到图4中的△COF，证法如下.

证法3：如图4，以点O为旋转中心，把△AOE绕点O按顺时针方向旋转180°，得到△COF.

由于∠AOE+∠EOC=180°，∠FOC=∠AOE，所以∠FOC+∠EOC=180°，所以E、O、F三点共线.

这种证法实际上是在旋转中位线OE所在的△AOE，观察图2知道OE也是△ABO内部的线段，还可以从旋转△ABO来证明定理.

证法4：如图5，以点O为旋转中心，把△ABO绕点O按顺时针方向旋转180°，得到△CDO，此时EO转到了FO的位置.

则由旋转性质，易证E、O、F三点共线，B、O、D三点共线，BE∥DF，BE=DF，所以四边形BEFC为平行四边形，得出结论.

由于EO是△ABC内部的线段，直接旋转△ABC来进行定理证明.

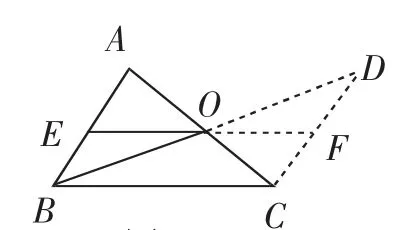
图5

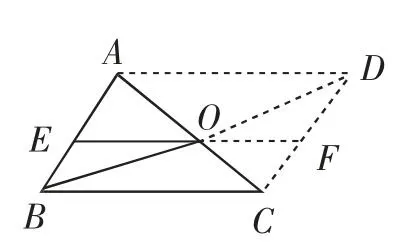
图6

证法5：如图6，以点O为旋转中心，把△ABC绕点O按顺时针方向旋转180°，得到△CDA，此时EO转到了FO的位置.

则由旋转性质，易证E、O、F三点共线，且四边形BEFC、AEFD均为平行四边形，得出结论.

设计意图：以学定教应关注学生的两个水平：一是学生现有水平，即学生独立活动时所能达到的解决问题的水平；二是学生可能的发展水平，也就是通过教学所获得的潜能，这种潜能正是学生发展的可能性，是教学应该利用的，更是来自学生自身思维的积极力量.学生感受到三角形与平行四边形知识之间相互联系的同时，多角度环环相扣思考构造▱BCFE，探索多种证法，发展了学生的发散思维.

刚才通过取平行四边形中的一个三角形，从整体到部分来探究证法，也可以从部分到整体来探究定理的证明.

2.三角形剪拼平行四边形

活动2：将图7中的△ABC沿中位线剪开分成两部分，拼成了一个四边形.剪下的△ADE有图8、9所示的两种拼法.

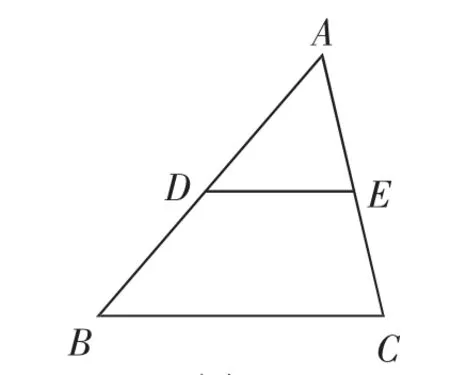
图7

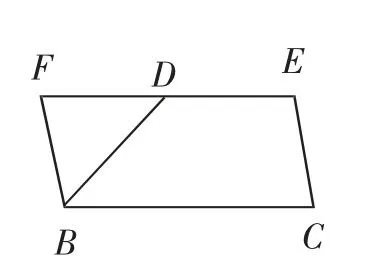
图8

图9

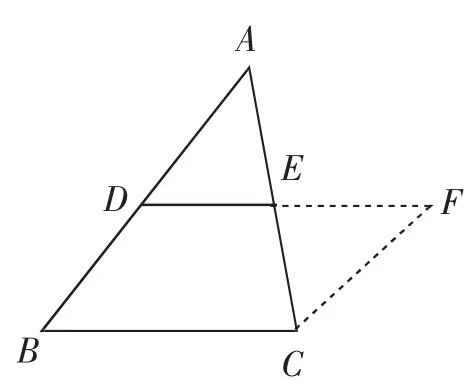
图10

发现：以图9 为例，图7 中的△ABC 中，∠AED+∠CED=180°，图9中的∠FEC就是图7中的∠AED，所以∠FEC+∠CED=180°，所以D、E、F三点共线.

因为∠ADE=∠F，所以DB∥CF.

由中位线定义知道AD=DB，且AD拼到图9中的CF处，所以DB=CF.

即DB与CF既平行又相等，所以四边形BCFD为平行四边形.于是得到中位线DE∥BC，DF=2DE=BC，所以△ABC的中位线平行于第三边，并且等于第三边的一半.

猜想：由刚才的操作、推理、验证，我们知道了△ABC的中位线平行于第三边，并且等于第三边的一半，猜想任意三角形的中位线都具有这样的性质.

验证：结合拼图，得到启示，证明的关键是构造出图10中的▱BCFD，即得到图10中的EF、CF这两条辅助线.这时可以像证法1、2、3那样进行.虽然上述三种证法不同，但都是先由全等三角形，得到DF与AC互相平分，这使得学生自然联想到对角线互相平分的四边形为平行四边形，也就是说还可以这样来证明.

证法6：如图11，延长DE至点F，使得DE=EF.连接CF、AF、CD.

由AE=EC，DE=EF，得到四边形ADCF是平行四边形，则有AD∥FC，AD=FC.

由中位线定义知DB=FC，则四边形BCFD是平行四边形，得出结论.

当然也可以像证法3、4、5那样，通过旋转法进行证明.

设计意图：证明教学应以寻找证题思路为核心.两个活动，意在将抽象问题具体化，给定理的证明引出思路.迥然不同的活动却可以用同样的证法，活动2让学生再次经历寻找证明思路的过程，学生学寻找方法、学研究问题的一般方法，学感受的数学知识、方法间存在的本质联系.最好的学习方法是做中学，这种学的过程推动着学生思维发展，道是无意实有意地学会从多角度思考.

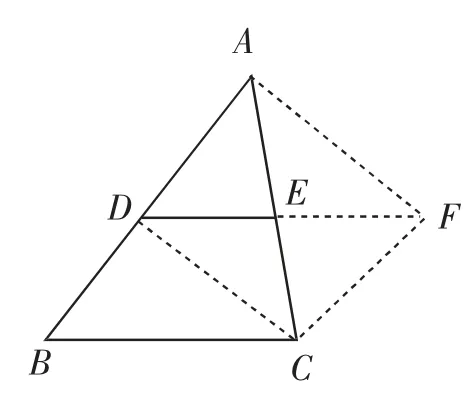
图11

图12

3.证法归本，模型助思

定理是要证明两条线段间的数量和位置关系.数量问题是证明线段的倍分问题，通常采用截长补短法；位置问题是证明平行关系，通常利用“三线八角”中角的关系.

以上不同证法均是通过中点倍长法补短，在△ABC的形外构造▱BCFD.这使得我们思考能否采用截长法，如图12，取BC的中点F，来证BF=FC=DE，连接EF，证四边形BDEF为平行四边形.由八年级学生的数学现实，结合已知条件无法证明这一想法.

而图12由于截长，在△ABC的形内构造了四边形BFED.如果将图12摆放成图13所示的位置，图13中EF与CB和图10中DE与AC都是三角形一条中位线与一边，图12中FE就相当于图10中的DE，于是想到延长线段EF或者FE构造出与图10类似的几何模型.延长线段EF得到图14，又有如下两种证法.

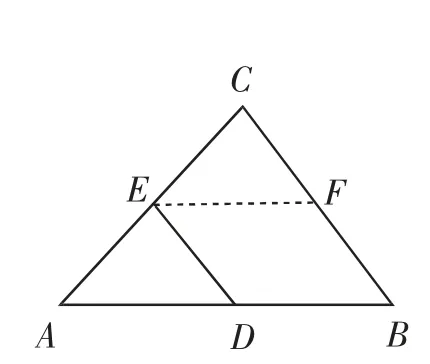
图13

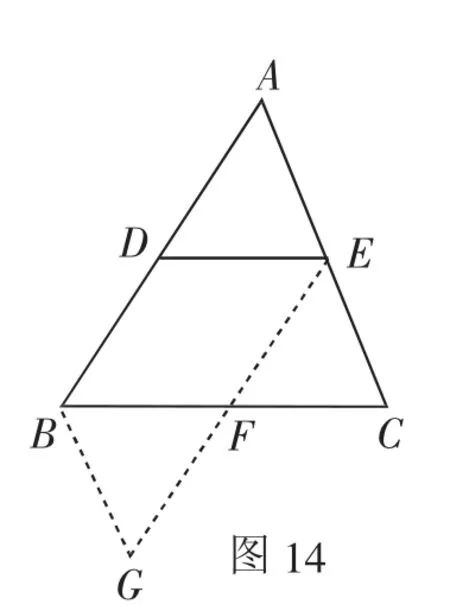
图14

证法7：取BC的中点F，连接EF并延长至点G，使得FG=EF，连接BG.

证法8：过点E作AB的平行线交BC于点F，过点B作AC的平行线交FE于点G.

先证四边形ABGE是平行四边形，再得到△BFG△CFE，证得四边形DBFE是平行四边形，得出结论.

本文引导学生探寻的各种证法，是依据八年级学生的数学现实，以所学内容自然延伸和必要发展为前提，以以旧引新为基础，以直观图形探抽象证明为手段，通过已有的证明经验和方法，完成定理证明.证法可归纳为三类：倍长法、平行线法、旋转法，实际上倍长法、平行线法都可以借助旋转来实现.

设计意图：指向数学本质，激发学生深度思考，必将助推学生思维发展.由直观图形得到启示得出六种不同证法；再由定理的结论出发采用分析法，探寻证明的通法；类比补短法来探索截长法，易于化陌生为熟悉，化难为易；通过在三角形形内和形外同时构造平行四边形，证明结论，促进学生深度思考.证明思路的拓展，其实质就是从知识到方法的迁移，发展了学生的创造性思维.

三、教学思考

数学家波利亚曾说过：教师讲了什么并不重要，但更重要千万倍的是学生想了什么，学生的思路应该在学生自己的头脑中产生，教师的作用在于系统地给学生发现事物的机会.“以学定教”让我们实现了“思维发展永远不能被教给，应是在学生自己建构理解知识过程中习得”.通过创设图形旋转与剪拼活动，设置符合学生数学现实的问题，让学生经历动手操作、观察思考、发现结论、提出猜想等思维过程.由活动开始找准学生思维的起点，唤醒学生的思维，激发学习欲望；由活动结果，引导学生从不同角度思考如何添辅助线，探索验证过程，激发学生深度思考；随着证法的不断增多和加深，学生的思维也逐渐深入发展，类比得到截长法验证定理，学生在不断探索证明过程中，收获对方法和策略的领悟，思维被推向顶峰.