几何图形邂逅函数图象——以“动点+面积+图象”问题为例

（江苏省睢宁县第二中学）

函数是中学阶段数学学习的核心内容.几何图形与函数图象相结合的动态问题覆盖知识面广，综合性强，能够有效考查学生分析问题、解决问题的能力，体现学生的核心素养，备受中考命题者的青睐.笔者认真研究了江苏省徐州市历年的中考试题，发现从2010年到2017年中有五次考查了“动点+面积+图象”问题，即由于点在几何图形上的运动引起了三角形面积的变化，从而形成了函数关系.在教学中，学生对这样的题目总是感到束手无策，看不懂问题，也不知道为什么这样做.本文以江苏省徐州市中考试题为例，从点的运动方式、问题的突破口和问题的实质三个方面来阐述解决这类问题的策略.

一、单动点引起的一次函数变化

例1（2011年）如图1（1），在△ABC中，AB=AC，BC=acm，∠B=30°. 动点P以1 cm/s的速度从点B出发，沿折线B—A—C运动到点C时停止运动，设点P出发xs时，△PBC的面积为ycm2，已知y与x的函数图象如图1（2）所示，试根据图中信息，解答下列问题.

图1

（1）试判断△DOE的形状，并说明理由；

（2）当a为何值时，△DOE与△ABC相似？

点的运动方式：由于点P的运动引起了△BPC面积的变化.其中，△BPC的底边BC长是不变的量，BC边上的高是随着时间x的变化而变化的量，因此△BPC的面积y是关于运动时间x的函数.在这个变化过程中，OD表示点P在边BA上运动时面积随着时间的增加而增加的一次函数关系，DE表示点P在边AC上运动时面积随着时间的增加而减少的一次函数关系.

问题的突破口：由于AB=AC，且点P的运动速度不变，故上升和下降所用的时间相同，所以△DOE是等腰三角形.当点P运动到点A时面积最大，点D的纵坐标就是△ABC的面积.

问题的实质：两个等腰三角形的底边和底边上的高对应成比例，两个三角形相似，即当△ABC的面积与底边上的高的数量之比等于点P运动所用的时间（即OE的长度）与底边BC的数量之比时，等腰△ABC与等腰△DOE相似.

解：（1）△DOE是等腰三角形.

如图2，过点D作DF⊥OE，垂足为点F.

因为AB=AC，

所以点P在AB，AC上运动的时间相同.

所以F是OE的中点.

所以DF是OE的垂直平分线.

所以DO=DE.

所以△DOE是等腰三角形.

图2

图3

（2）如图3，过点A作AG⊥BC，垂足为点G.

【评析】此题在“动点+面积+图象”的基础上考查了等腰三角形的判定、解直角三角形，以及相似三角形的判定.把函数图象和等腰三角形结合起来，明确点的运动方式和函数中两个变量之间的变化关系，找到隐藏的突破口——上升和下降所用的时间相同，以及临界点D的纵坐标就是△ABC的面积，运用相关知识解决问题.

二、双动点引起的一次函数和二次函数变化

1.双动点同时出发

例2（2014年）如图4（1），在正方形ABCD中，点P沿边DA从点D开始向点A以1 cm/s的速度移动；同时，点Q沿边AB，BC从点A开始向点C以2 cm/s的速度移动.当点P移动到点A时，点P，Q同时停止移动.设点P出发xs时，△PAQ的面积为ycm2，y与x的函数图象如图4（2）所示，则线段EF所在的直线对应的函数关系式为_____.

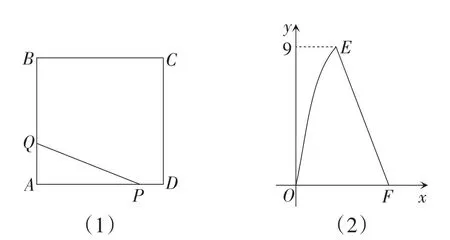
图4

点的运动方式：由于点P，Q的运动引起了△APQ面积的变化.在这个变化过程中，△PAQ的边AP的长是变量，当点Q在AB上运动时，AP边上的高AQ的长是变量，它们都是随着时间的变化而变化，因此△PAQ的面积y是关于运动时间x的二次函数；当点Q在BC上运动时，AP是变量，AP边上的高即正方形的边长，是常量，此时y是关于运动时间x的一次函数.可见，图4（2）中的曲线OE表示点P在AD上而点Q在AB上运动时的函数图象，线段EF表示点P在AD上而点Q在BC上运动时的函数图象.

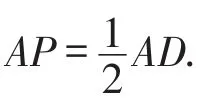
问题的实质：根据点Q到达点B、点P到达AD中点以及△PAQ面积的最大值（点E的纵坐标）之间的数量关系求出边长和运动时间，确定点E和点F的坐标.

解：设正方形的边长为acm.

当点P到达AD的中点时点Q到达点B，

解得a=6.

此时运动的时间为3 s.

所以点E(3，9)，F(6，0).

所以线段EF所在的直线对应的函数关系式为y=-3x+18.

【评析】此题考查了运用待定系数法求函数表达式.由于正方形的边长未知，这给解题带来了一定的难度，需要结合图4求出正方形的边长和临界点E，F的坐标.曲线OE实际是抛物线的一部分，点E恰好是顶点，还可以求出该曲线对应的函数表达式.当然，也可以根据三角形的面积公式确定相应的函数表达式.

例3（2010年）如图5（1），在梯形ABCD中，∠C=90°.动点E，F同时从点B出发，点E沿折线BA—AD—DC运动到点C时停止运动，点F沿BC运动到点C时停止运动，它们运动时的速度都是1 cm/s.设点E，F出发ts时，△EBF的面积为ycm2.已知y与t的函数图象如图5（2）所示，其中曲线OM为抛物线的一部分，MN，NP为线段.试根据图中的信息，解答下列问题.

（1）梯形上底的长AD=____，梯形ABCD的面积=____；

（2）当点E在BA，DC上运动时，分别求出y与t的函数关系式（注明自变量的取值范围）；

（3）当t为何值时，△EBF与梯形ABCD的面积之比为1∶2.

图5

点的运动方式：由于点E，F的运动引起了△EBF面积的变化.在这个变化过程中，当点F在BC上运动，且点E在BA上运动时，底边及底边上的高是变量，它们都是随着时间的变化而变化，因此△EBF的面积y是关于运动时间t的二次函数，其图象对应图5（2）中的曲线OM；当点F到达点C时，点E到达点A，随后点E在AD上运动，此时△EBF的面积不变，对应图5（2）中的线段MN；当点E在DC上运动时，△EBF的底边BF不变，高在变化，因此△EBF的面积y是关于运动时间t的一次函数，其图象对应图5（2）中的线段NP.

问题的突破口：结合图5（2）可知，当运动时间为5 s时，点E，F同时到达点A，C，即BA=BC=5 cm，此时△EBF的面积是10 cm2，说明梯形ABCD高为4 cm；线段MN表示点F到达点C停止运动，点E在AD上再运动2 s，可知AD=2 cm；线段NP表示点E在DC上运动时的函数图象，再运动4 s到达点C，故点P(11，0).运用待定系数法很容易求得相应的函数表达式.

问题的实质：求AD的长、梯形的面积及函数表达式就是要明确点E，F运动的方式和其在相应边上运动的时间；求t为何值时△EBF与梯形ABCD的面积之比为1∶2，就是两个函数值都是梯形面积一半时对应的时间.

解：（1）2 cm，14 cm2；

（2）方法1：当0 ≤t≤ 5时，设y=at2，

方法2：①如图6，当点E在BA上运动时，此时0≤t≤5.

图6

图7

②如图7，当点E在DC上运动时，此时7≤t≤11.

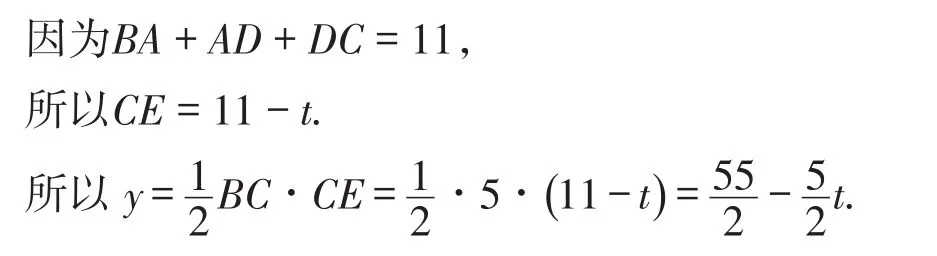
（3）由已知条件可求得S梯形ABCD=14.

【评析】此题需要学生具有较强的识图能力，把梯形和函数图象结合起来寻找问题的突破口，即判定BC=BA=5 cm，梯形的高为4 cm，点E的运动时间为11 s，考查了用待定系数法求函数表达式，相似三角形的判定和性质，根据函数表达式求函数值，以及数形结合、分类讨论的数学思想.

2.双动点先后出发

例4（2017年）如图8（1），在菱形ABCD中，AB=5 cm，动点P从点B出发，沿折线BC—CD—DA运动到点A停止，动点Q从点A出发，沿线段AB运动到点B停止，它们运动的速度相同，设点P出发xs时，△BPQ的面积为ycm2，已知y与x之间的函数关系如图8（2）所示，其中OM，MN为线段，曲线NK为抛物线的一部分，试根据图中的信息，解答下列问题.

（1）当1＜x＜2时，△BPQ的面积____（填“变”或“不变”）；

（2）分别求出线段OM，曲线NK所对应的函数表达式；

（3）当x为何值时，△BPQ的面积是5 cm2？

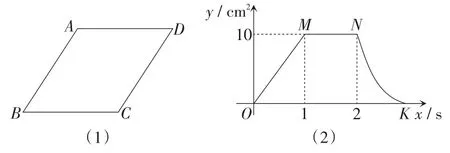
图8

点的运动方式：由于点P，Q的运动引起了△BPQ面积的变化.这两个点是同时出发还是先后出发？观察图8（2），线段OM表示一次函数图象的一部分（即△BPQ底边和底边上的高一个变化一个不变），可知点P一定是先出发的，出发1 s到达点C；线段MN表示面积不变（即△BPQ底边和高都不变），可知点P从点C到达点D又用时1 s，在这个过程中，点Q始终在点A处不动；曲线NK为抛物线的一部分（即△BPQ底边和高都变），此时点P在DA上运动，点Q在AB上运动，再运动1 s各自到达终点.

问题的突破口：通过上述分析，点P在DA上运动，且点Q在AB上运动，△BPQ底边BP及其边上的高都在减小，面积随着时间的增大而减小；在到达终点后假若点P，Q继续沿着射线AB，DA运动，△BPQ底边BP及其边上的高都将增大，面积随着时间的增大而增大，所以点K(3，0)恰好是抛物线的顶点；观察函数图象，点O，M，N的坐标已知，运用待定系数法可求得OM，NK对应的函数表达式.

问题的实质：明确点P，Q的运动方式，确定点K的坐标及其顶点的身份，以及当函数值为5时对应的自变量x的值.

解：（1）不变；

（2）方法1：设线段OM的函数表达式为y=kx.

把(1，10)代入，得k=10.

所以线段OM的函数表达式为y=10x(0≤x≤1).

根据题意，可得K(3，0).

设曲线NK所对应的函数表达式y=a(x-3)2.

把(2，10)代入，得10=a(2-3)2.

解得a=10.

所以曲线NK所对应的函数表达式为y=10(x-3)2.

方法2：根据题意，可知点Q到达点C用时1 s，点P，Q的速度均为5 cm/s，BQ=BF=5xcm.

如图9，分别过点A，C作AE⊥BC，CF⊥AB，垂足分别为点E，F.

由△ABC的面积为10 cm2，得

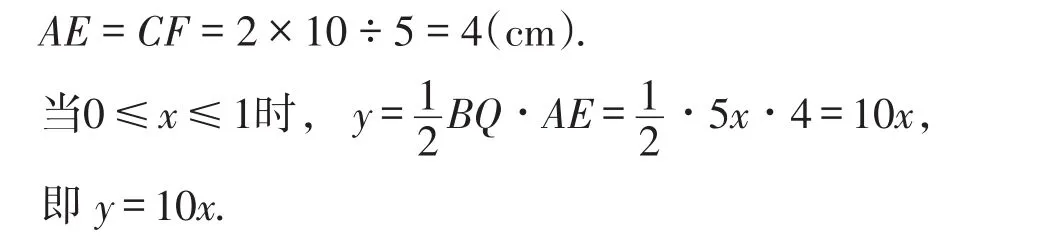
如图10，当2≤x≤3时，过点Q作QG⊥BA，垂足为点G.

图9

图10

（3）把y=5代入y=10x，得

【评析】此题与例3相比，最大的不同是没有告诉两个动点是先后出发还是同时出发，这给确定点的运动方式带来了较大的麻烦.既需要学生具有较强的识图能力，又需要学生具备分析问题、解决问题的能力，数形结合、分类讨论，充分体现了对学生数学核心素养的考查.不难发现这类问题在理解函数本质的基础上根据函数图象确定点的坐标，利用待定系数法求函数表达式，比起利用三角形的面积公式、相似三角形的性质寻求数量之间的关系来确定函数表达式要更加的简单.

总之，解决这类图形和图象结合的问题，首先要明确点的运动方式，点在图形中怎样运动，对应的函数图象是怎样的，明确变化过程中的常量和变量，这是解决问题的前提条件；其次，要理解函数图象中临界点表示的实际意义，寻找解决问题的突破口，这是解决问题的关键；最后，要理解所求问题的实质，明确运用哪些知识点和数学思想、方法，这是解决问题的保证.

三、展望与思考

通过动点在几何图形上的运动，把三角形的面积和点运动的时间或路程之间的变化关系用函数图象刻画出来，将图形和图象融为一体.图形中直观体现了点的运动方式，图象中则蕴含了变量之间的变化关系.在这些变化关系中考查函数、等腰三角形、相似三角形、勾股定理、解直角三角形等数学核心知识，既考查基础知识和基本技能，又对学生的抽象能力、推理能力、运算能力，以及数形结合、分类讨论、函数建模等数学思想方法的运用有着较高的要求，体现了学生的核心素养水平.

展望未来，这类问题依然会受到命题专家的青睐.我们可以把初中阶段常见的几何图形，诸如等腰三角形、直角三角形、平行四边形、矩形、菱形、正方形、等腰梯形、直角梯形或圆等，与一次函数、二次函数、反比例函数有机结合，通过动点在几何图形上的运动，或者点与其对称点的运动，或者点与线的双动等引起的函数变化关系来考查核心知识，以及学生分析问题、解决问题的能力水平.

各地的中考命题对教学起到了导向的作用.因此，在平时的教学中，要减少单纯记忆、机械训练，注重引导学生理解函数的本质以及相关的概念、定理，扎实的掌握基础知识；注重解决问题的方法、策略培养训练，让学生积累“会用数学眼光看问题，会用数学思维思考问题，会用数学语言表达问题”的数学活动经验，即“会看、会想、会说”，引领学生从过程中提炼方法，从方法中感悟思想，最终实现数学思维能力的提升，只有这样才能有利于学生的发展.