Tietze 扩张定理在子基正规空间的推广

蔡巧琳

（闽南师范大学数学与统计学院,福建漳州363000）

1982 年波兰数学家Z.Pawlak 在文献[1]中提出粗糙集理论后，文献[2]将其推广到覆盖广义粗糙集理论.通过研究覆盖粗糙集与拓扑空间的关系，文献[3]给出了拓扑空间中子集关于子基的内部算子和闭包算子的定义，进而导出了关于子基的开集、导集、闭集、边界等基本概念.在文献[3]的基础上，许多文章对一般拓扑学中的部分拓扑性质做了推广.其中，文[4]给出了关于子基的连通性概念和其具有的性质.文献[5]给出了拓扑空间关于子基的正则、正规、完全正则等概念，并研究它们的性质.文献[6]定义了子基第一正规空间和子基第二正规空间概念，并给出了Urysohn 引理在子基第一、第二正规空间上的推广.基于以上理论基础，本文主要研究将Tietze 扩张定理分别推广到子基第一正规空间和子基第二正规空间，并给出推广后的定理及证明.

1 预备知识

以下定义与定理为证明过程中所需用到的理论基础和主要结论.设为 X 上的拓扑， β 为的子基，以下简记为（X，，β）.

定义1[3]设（X，，β）为拓扑空间，AX，若 dβ（A）=A，则称 A 为 β 闭集.

定义1[3]设（X，，β）为拓扑空间，x∈X，U∈X，如果存在一个包含 x 的 β 开集 V 包含于 U，即存在V∈β使得 x∈VU，则称 U 为 x 的 β 邻域.点 x∈X 的所有 β 邻域构成的 X 的子集族称为点 x 的β 邻域系，记为 Uβ，x.

定理1[3]设（X，， β）为拓扑空间，则有对于任一 x∈X， Uβ，x≠.

定理1 为 β 邻域具有的性质，即任一点 x∈X， β 为的子基，都会存在x 的 β 邻域.

定义3[4]设（X，1，α）与（Y，2，β）是两个拓扑空间，映射 f：X→Y.如果 Y 的每一个 β 开集 U的原像 f-1（U）是 X 的 α 开集，则称 f 为（α， β）连续映射.

下面给出f 为（α，β）连续映射的等价性刻画.

定理2[4]设（X，1，α）与（Y，2，β）是两个拓扑空间，映射 f：X→Y.若 f 为（α，β）连续映射的充要条件为 Y 的任一 β 闭集 F 的原像 f-1（F）是 X 的 α 闭集.

为了推广Tietze 扩张定理，首先给出关于子基的第一、第二正规空间的定义.

定义4[6]设（X，，β）为拓扑空间，如果对 X 任意两个不交的 β 闭集 A、B，存在 β 邻域 U、V，使得AU，BV，且 UV＝，则称X 是关于子基的第一正规空间.

定义5[6]设（X，，β）为拓扑空间，如果对X 的任意两个不交的闭集 A、B，存在 邻域β 邻域 U、V，使得AU，BV，且 UV＝，则称X 是关于子基的第二正规空间.

证明过程中需要两同胚空间的子基之间的相互转化，通过文献[5]给出定理3.

定理3[5]设（X，1）和（Y，2）同胚，同胚映射为 h， β 是1的子基，h（β）＝｛h（A） A∈β｝为2的一个子基.

定义6[5]若（X，，β）是拓扑空间， （Y，Y， βY）是其子空间.如果 Y 是 βY正规空间，则称 Y 是X 的子基第一正规子空间.

定理4[5]若（X，，β）是一个β 正规空间，则它的每个β 闭子空间是β 正规空间.

这里的β 正规空间即X 关于子基的第一正规空间.则由定理4 有若（X，，β）是一个子基第一正规空间， Y 是 X 的 β 闭子集，若 A、B 是 Y 的两个不交的 βY闭子集，则 A、B 是 X 的两个不交的 β 闭子集.

最后通过文献[6]给出在子基第一、第二正规空间上推广后的Urysohn 引理.

定理5[6]设（X，， β）是一个拓扑空间， ［a，b］是 R 的闭区间， α 是［a，b］的子基.则 X 是子基第一正规空间的充要条件是对 X 任意两个不交的 β 闭集 A 和 B，存在一个（β，α）连续映射 f：X→［a，b］，使得 x∈A 时， f（x）=a； x∈B 时， f（x）=b.

定理6[6]设（X，， β）是一个拓扑空间， ［a，b］是 R 的闭区间， α 是［a，b］的子基.则 X 是子基第二正规空间的充要条件是对X 的任意两个不交的闭集A 和B， 存在一个 （β，α） 连续映射f：X→［a，b］，使得 x∈A 时， f（x）=a； x∈B 时， f（x）=b.

2 Tietze 扩张定理在两个子基正规空间的推广

为了将Tietze 扩张定理推广到子基第一正规空间和子基第二正规空间，先给出相关引理及其证明.

以下验证映射g*满足引理1 要求：设x∈A.如果因此当如果有综上可得

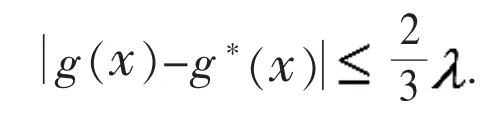
以下验证映射g*满足引理2 要求：设x∈A.如果综上可得

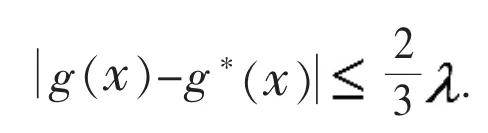
下面给出在子基第一正规空间上推广后的Tietze 扩张定理及其证明.

证明 由于［a，b］同胚于［－1，1］，所以取［a，b］=［－1，1］证明即可.

充分性 设 B 和 C 是 X 中任意两个不交的 β 闭集，令 BC=A.定义 A 上的（βA， α）连续映射f：A→［－1，1］使得当 x∈B 时，有 f（x）=-1；当 x∈C 时，有 f（x）=1.由定理条件知 f 有一个（β，α）连续扩张映射 g：X→［－1，1］.显然当 x∈B 时，有 g（x）=-1；当 x∈C 时，有 g（x）=1.则根据定理 5可得X 是子基第一正规空间.

必要性 设 X 是子基第一正规空间，A 是 X 中的 β 闭集，f：A→［－1，1］是一个（βA，α）连续映射.接下来用归纳的方式对于每一个n1 定义一个（β，αn）连续映射对每一个n0 定义一个（βA，h（αn））连续映射其中，实数空间的子空间均为同胚空间，设它们的同胚映射为h.

令 f0=f.对于 n ＞0，假设连续映射 fn-1已经定义.由引理2 知存在（β，αn）连续映射 gn使得对于任何并且定义映射 fn使得对于每一个 a∈A，有 fn（a）=fn-1（a）-gn（a）.显然映射 fn是（β， αn）连续映射.根据归纳原则映射序列｛fn｝n0和映射序列｛gn｝n1均已定义.

定义映射 g：X→［－1，1］，使得对于每一个 x∈X 有设 x∈X.由于对于每一个 n收敛，并且收敛于［－1，1］中的点.因此映射 g 的定义是确切的.

接下来要验证映射 g 满足定理要求.首先验证映射 g 是映射 f 在 X 上的一个扩张.设 a∈A.对于每一个整理可得由于 fn：A→即可得在上式中令 n→∞， 可得f（a）=f0（a）=g（a）.

接下来验证映射 g 是（β，α）连续映射，设 x 是X 中任意一点，对于任意给定的实数＞0.选取整数 N＞ 0 ，使得对于每一个 n=1，2，…，N，由于gn是（β， αn）连续映射，再由定理 1可知存在 x 的一个 β 邻域，设为 Un，使得当 y ∈Un时，有于是，当 y ∈U1时，有

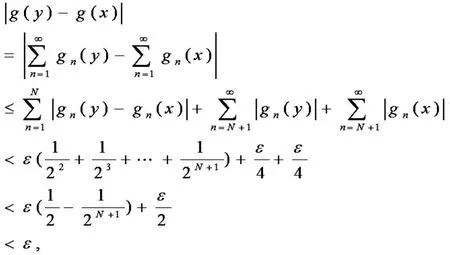
综上所述，即证明了映射 g 在点 x 处的连续性.由于 x 是X 任意一个点，所以映射 g 是一个（β，α）连续映射.

以下定理是Tietze 扩张定理在子基第二正规空间上的推广.

证明 由于［a，b］同胚于［－1，1］，所以取［a，b］=［－1，1］证明即可.

充分性 设A 和 B 是 X 中两个不交的闭集.定义映射 f：AB→［－1，1］，使得当 x∈A 时，有f（x）=－1；当 x∈B 时，有 f（x）=1.可见 f 为连续映射.由定理条件知 f 有一个（β，α）连续映射 g：X→［－1，1］.那么当 x∈A 时，有 g（x）=－1；当 x∈B 时，有 g（x）=1.则由定理 6，可得 X 是子基第二正规空间.

必要性 设X 是子基第二正规空间，A 是X 中的闭集， f：A→［－1，1］ 是一个连续映射.接下来用归纳的方式对每一个n0 定义一个连续映射和对于每一个 n1 定义一个（β，αn）连续映射

令 f0=f.对于 n＞0，假设连续映射 fn－1已经定义.由引理2 知存在（β，αn）连续映射 gn，使得对于任何并且定义连续映射 fn使得对于每一个 a∈A 有 fn（a）=fn－1（a）-gn（a） .显然映射 fn是连续的.根据归纳原则映射序列｛fn｝n0和映射序列｛gn｝n1均已定义.

定义映射 g：X→［－1，1］，使得对于每一个 x∈X 有设 x∈X，由于对于每一个［－11］g收敛，并且收敛于 ， 中的点.因此映射 的定义是确切的.

以下验证映射g 满足定理要求.首先验证映射g 是映射f 在X 上的一个扩张.设 a∈A.对于每一个整理可得n→∞f（a）=f在上式中令 .可得0（a）=g（a） .

接下来验证g 是（β，α）连续映射，为此设x 是X 中任意一点，对于任意给定的实数＞0.选取整数N ＞ 0 使得对于每一个 n=1，2，…，N，由于 gn是（β， αn）连续映射，由定理 1 可知存在 x 的一个 β 邻域，设为 Un，使得当 y ∈Un时，有于是，当 y ∈U1时，有

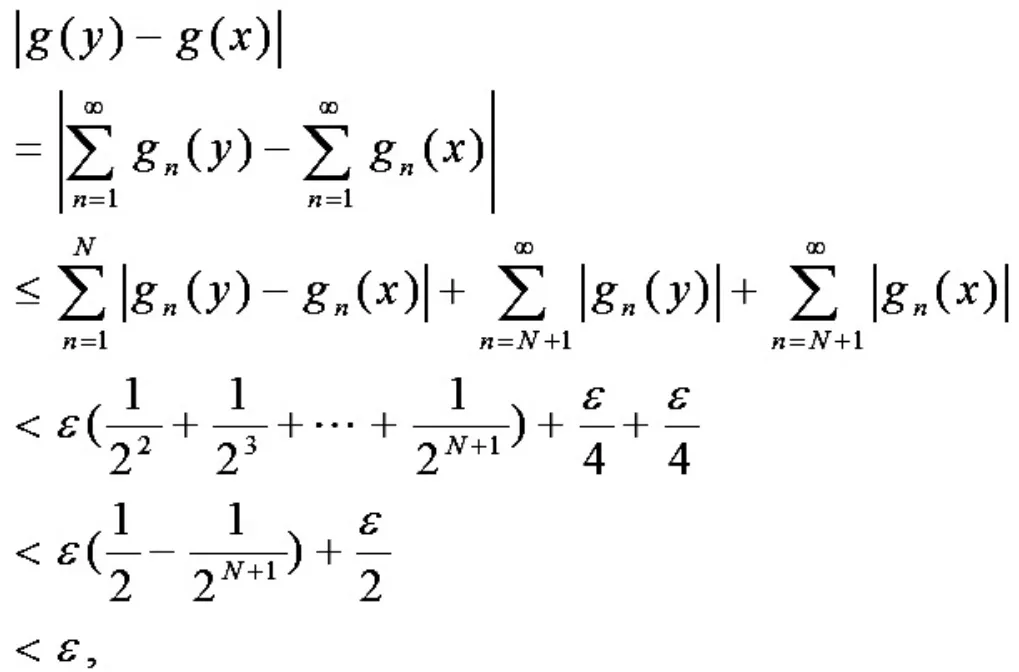
综上所述， 即证明了映射 g 在点 x 处的连续性.由于 x 是X 中任意一个点， 所以映射 g 是一个（β，α）连续映射.

3 结论

Urysohn 引理和Tietze 扩张定理都描述了正规性的函数刻画.文献[6]定义了子基第一、第二正规空间，并在子基第一、第二正规空间上证明了Urysohn 引理.本文在此基础上，将Tietze 扩张定理推广到子基第一正规空间和子基第二正规空间.