运用类比思想优化初中数学教学

吕琴

[摘 要] 进入初中以后，学生数学学的就不再仅仅是知识，还有方法和思想，三者相互联结，共同促进学生素养的提升。在新课改背景下，要加强对类比思想的渗透、运用，给学生提供良好的学习平台，让其在不断探究中深化知识理解，以此优化思维活动。

[关键词] 初中数学;类比思想;课堂教学

类比思想，简单来说就是分类对比，其本质是根据两个对象的相似属性猜想其其他属性存在的关系，可能是相同或者相似。这种思维方法的运用不仅能促进学生对知识的理解，还能培养其思维能力，以此提高课堂学习效率。“类比是一个伟大的引路人”，类比在数学中的重要性不言而喻，对于学生直觉思维、合情推理能力的提升有很大作用。

一、运用类比思想深化教材解读

类比作为一种重要的思维方法和推理方法，在数学发展的历史长河中占有举足轻重的地位。这一点在教科书中就有着重体现。在教学时可加以提醒，让学生充分意识到这种思想的广泛应用。

如一元一次不等式是初中数学教学的重难点，在讲解这一知识时，就可与一元一次方程类比。在这一过程中，学生能清楚发现其定理、性质以及运算过程都存在相似性。抓住这一点，就能大大降低认知难度，让教学达到事半功倍的效果。又如，度、分、秒的运算及注意事项可与时、分、秒类比，这样一来学生就能快速掌握。学生经常受到类比思想的熏陶，对这一数学思想不再陌生，就能在理解的基础上尝试运用。[1]

借助教材的解读，不仅能让学生意识到类比思想的普遍性，还能优化教学，让学生在不断思考中尝试运用，以此降低解题难度，并在这一过程中激发对数学学习的兴趣，在兴趣引导下不断深入，以此提高教学效率。

二、运用类比思想活化数学课堂

类比法在数学教学中的运用十分广泛，主要体现在概念教学、定理教学以及运算法则上。意识到这一点，在教学中就要加强重视，积极引导，借助这一思想不断激励学生，让其在探究中深化思考，扎实掌握要点。[2]

（一）借助类比理解概念

概念作为研究事物的基础与关键，在初中数学教学中占有重要位置，不容忽视。在教学中运用类比，不仅能沟通新旧知识，发挥显著的桥梁作用，还能促进概念与思想的类比，以此激励学生，使其在熟悉的氛围中积极探究，以此消除抵触心理，乐于花时间、精力学习，以此提高课堂效率。

如在教学分式基本概念及性质时，就可引导学生回顾分数，让其将两者进行比较，寻找相似与不同之处。在这一过程中，首先可提问学生：“小学里我们学过分数。什么叫分数？分数有什么性质？”对此，学生十分积极回答，讨论交流后得出结论：两个整数相除的式子叫分数，分数的分母不能为零。分数的分子和分母同时乘（或除以）一个不为零的数，分数的值不变。这时，就可借助类比导入：“在学完用字母代表数之后，可将分母里含有字母的式子叫分式……”由此，学生便能清楚分式与分数之间的关系，顺利激活原有认知结构，为新知学习做好铺垫。在这一过程中，为了强化类比，可适当追问：“你认为分式中的字母有没有限制条件？为什么？”以此揭示分式有无意义的条件，开启教学。这样一来，便能让原本抽象、生涩的概念变得浅显易懂，也让学生在自主探究中加深对内容的理解，以此完善认知，无形中提升学科素养。

（二）借助类比启发探究

除了概念教学之外，类比思想在数学定理与运算法方面的运用也十分广泛。对此，就可培养学生思维能力，以此落实能力培养目标。

如在教学“相似三角形的判定”时，就可先复习“全等三角形的判定定理”，以此展开教学。首先，让学生自主回顾：全等三角形的判定定理有哪些？随后借助小组交流完善思考，得出结论：有边角边定理（即SAS）、角边角定理（即ASA）、角角边定理（即AAS）、边边边定理（即SSS）。这时大多数学生还会忽略直角三角形中的斜边直角边定理（即HL），对此就要稍加提醒。回顾之后，就可点拨学生：对于相似三角形的判定，是否也存在类似定理呢？这样一来，便能充分调动学生，让其在类比方法引导下开启新知学习，根据两者的相似之处探究，在思考、交流中深化知识理解，以此完善认知，让教学达到预期效果。在这一过程中，要加强对学生的指导，在关键处启发学生，以此发挥学生能动性，促进新知理解、吸收。

三、运用类比思想简化中考试题

在应试教育背景下，中考是学生无法避免的，在面对这样一场大型考试时，要想取得骄人的成绩，学生不仅要有扎实的基础，更要具备较强的综合能力，能灵活运用所学，以此提高解题效率，在速度与正确率上赶超他人。[3]

（一）条件类比寻找突破

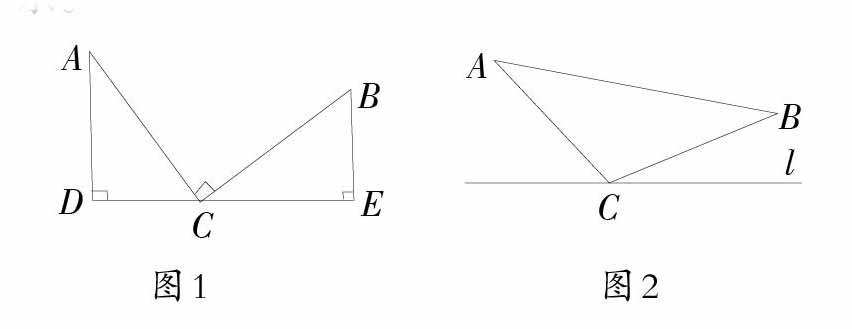
所谓“条件类比”，即是两个对象，可以是定理、公式或者法则等之间有条件关系，将其展开类比。这一过程主要考查学生逻辑思维能力。下面就以中考常见的“一线三直角问题”为例展开具体探究。首先，呈现问题背景：如图1，[AD⊥DE，BE⊥DE，C]是线段[DE]上一点，且[AC⊥BC，AC=BC]，试求图中线段和角的数量关系。

这一题难度较小，学生在解决过程中没有多大阻碍，对此就可类比迁移，适当增加难度，以此拓展：如图2，△ABC是等腰三角形，[AC=BC，∠ACB=α，]直线[l]经过顶点[C]，且在三角形外部，请添加适当的辅助线（不经过点[C]），构造一对全等的三角形。

借助这两题的类比，就能提供学生自主突破的空间，让其在掌握基础的前提下全面思考，充分利用全等三角形知识解题，在这一过程中尝试借助条件寻找突破口，以此解决问题，提高应试能力，促进综合素养发展。

（二）性质类比凸显思维

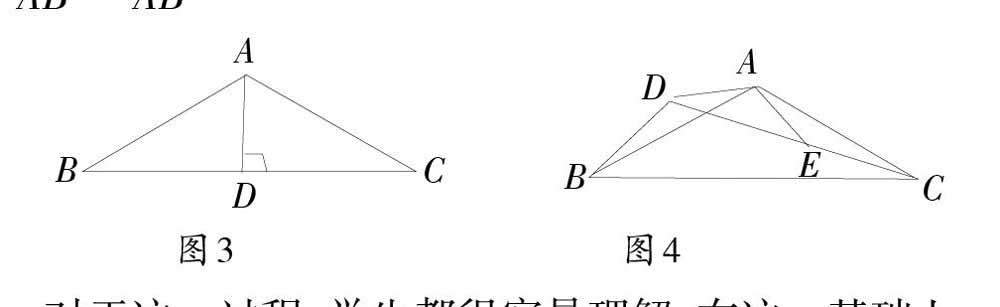
这种类比是根据对象的相同或者相似进行类比，主要考查学生思维能力以及对知识的掌握情况。这种题型在中考中大多是压轴题，虽然考得不多，但是难度较大，所占分值也大。首先，呈现问题背景：如图3，在等腰△ABC中，[AB=AC，∠BAC=120°，]作[AD⊥BC]于点[D]，则[D]为[BC]的中点，[∠BAD=12∠BAC=60°。]于是[BCAB=2BDAB=3]。

对于这一过程，学生都很容易理解，在这一基础上就可适当迁移，以此类比思考：如图4，△ABC和△ADE都是等腰三角形，[∠BAC=∠DAE=120°]，[D，E，C]三点在同一条直线上，连接[BD]。（1）证明：△ADE[?]△AEC;（2）直接写出线段[AD，BD，CD]之间的等量关系式。

总之，类比思想的渗透是提升学生思维的有效途径，不仅能推动初中数学教学，让课堂活动更具探究性，还能充分发挥学生主体性，让其在类比过程中有所发现，以此培养自学与实践思考能力，最终实现自身素养的提升。

参考文献

[1]余智敏，何春玲.妙用“类比” 激发创新[J].中学数学，2016，（07）.

[2]吴永萍.借助类比，让数学学习真正走向自主[J].数学教学通讯，2018，（07）.

[3]陳美荣.浅析“类比思想”在初中数学教学中的应用[J].数学教学通讯，2018，（14）.

责任编辑 李杰杰