在教学中注重培养学生数学抽象核心素养

☉陕西省宁强县天津高级中学 刘金平

数学抽象是高中数学的六大核心素养之一，是指舍去事物的一切物理属性，得到数学研究对象的思维过程.抽象函数问题对于高中生来讲，难度比较大，不易理解，主要特点是抽象函数的解析式不确定.试题常将函数、方程、不等式和数列等知识结合在一起，考查学生对函数的主要性质（如单调性、周期性、奇偶性和对称性）的理解能力、逻辑推理能力和抽象思维能力，养成从特殊到一般，从具体到抽象的解题思维习惯.

一、运用函数性质解决问题，培养学生数学抽象概括能力

例1设（fx）是定义在R上的偶函数，其图像关于直线x=1对称，对任意的x1，x2∈]，都有（fx1+x2）=（fx1）·（fx2），且（f1）=a＞0.

（2）证明：（fx）是周期函数；

分析：（1）这是根据题干条件求特殊值的问题，需要把1拆成，这样就可以直接利用条件进行求解；

（2）要利用图像的对称性找到对应关系并结合条件就能证明；

解析：（1）因为对于任意的x，x∈]，都有（fx+121x2）=（fx1）·（fx2）成立，

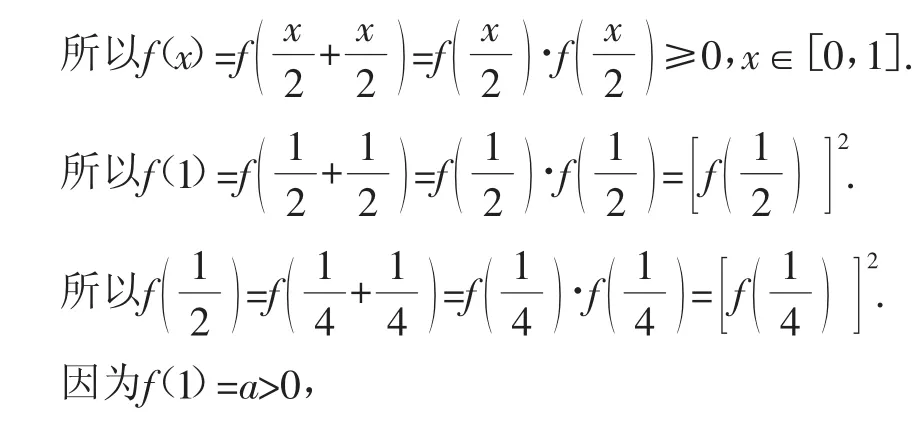
（2）证明：由题意可知，y=f（x）的图像关于直线x=1对称，故可得f（x）=f（2-x），x∈R.又由f（x）是偶函数知f（-x）=f（x），x∈R，所以f（-x）=f（2-x），x∈R.将上式中的-x用x替换，得到f（x）=f（x+2），x∈R，

则由周期函数的定义可知f（x）是R上的周期函数，且2是它的一个正周期.

（3）由（1）知f（x）≥0，x∈［0，1］，

由（2）知（fx）是以2为周期的周期函数，因此，an=

评注：该题主要考查学生对函数的概念、图像，以及奇偶性、周期性和对称性等重要性质的理解能力，以及递推数列等基础知识的运用能力；考查运算能力、数学抽象能力和逻辑推理能力.关键是要紧紧抓住题干条件f（x1+x2）=f（x1）·f（x2）进行适当变形寻找解决问题的突破口，巧妙地将抽象问题具体化.在解题过程中要让学生体会和感受到解决抽象函数问题的技巧和方法，从而达到落实数学核心素养的目的.

二、借助数学思想方法解决问题，培养学生数学抽象核心素养

例2已知函数f（x）对于任意的x，y∈R都有f（x+y）=f（x）+f（y），且当x＞0时，有f（x）＜0.

（1）求f（0）的值；

（2）判断f（x）的奇偶性与单调性，并证明你的结论；

分析：（1）由（fx+y）=（fx）+（fy）这个条件求特殊值，只需充分利用自变量取值的任意性就可以完成；

（2）结合题目条件，利用函数的奇偶性和单调性的定义巧妙地对（fx+y）=（fx）+（fy）进行变形即可；

解析：（1）由对于任意的x，y∈R都有f（x+y）=f（x）+f（y）成立，不妨令x=y=0，得

f（0+0）=f（0）+f（0），所以f（0）=0.

（2）根据函数奇偶性的定义，由（1）知，可令y=-x，得f（x-x）=f（x）+f（-x），

即f（0）=f（x）+f（-x），而f（0）=0，所以f（-x）=-f（x）.故f（x）为奇函数.

由函数单调性的定义，任取x1，x2∈（-∞，+∞），不妨设x1＞x2，则x1-x2＞0，由题设条件得f（x1-x2）＜0.

而f（x1-x2）=f（x1）+f（-x2），所以f（x1）+f（-x2）＜0，

即f（x1）＜-f（-x2）=f（x2）.所以f（x）在（-∞，+∞）上为减函数.

（3）因为函数（fx）是奇函数且当x＞0时，（fx）＜0，当x∈［-1，1），x-1＜0，得（fx-1）＞0，所以＜2k可变形为（fx2+1）＜2k（fx-1）.

①当k∈Z+时，由数学归纳法可证得2k（fx）=（f2kx）.（*）

②当k=0时，（*）式显然成立；当k＜0时，由奇函数的性质可证明（*）式也成立.

所以有（fx2+1）＜（f2kx-2k），由单调性得x2-2kx+1+2k＞0，对于x∈［-1，1）恒成立.运用分离参数法可变形为在x∈［-1，1）上恒成立，

评注：前两个问题采用“赋值法”就可以轻松解决，由定义域的一般性给变量赋特殊值即可，第三个问题则利用函数的单调性将抽象函数转化为求具体函数的最值问题，运用转化与化归的数学思想使问题得以解决，这是解决抽象函数问题的常用方法，在教学过程中要善于引导学生去感受、体会这种解题思路，不断积累经验，养成自觉运用数学抽象思维解决问题的良好习惯.

在高中数学课程的学习过程中，由于学生对高中数学知识的认知能力有限，还未形成系统的数学知识体系，从一个数学情境中抽象概括出一个数学模型的能力比较欠缺，这两个例子所给出的函数关系分别可以抽象为指数型函数f（x）=ax和一次函数f（x）=kx模型，这是学生最熟悉最易理解的两个函数模型，把抽象的不好理解的数学问题转化成学生熟悉的常见的数学问题，符合学生的认知规律，从而激发了学生学习数学的信心和兴趣，对培养学生学习数学的思维品质和提升学生的数学核心素养都有较大帮助.W