另辟蹊径，换角度思考优化解题策略

☉江苏省海门市第一中学 俞昉昉

数学是一门很灵活的学科，数学的知识点之间自成体系又互相关联，这给我们解决数学问题带来了更多选择，我们不仅可以利用最相关的知识点和最常用的方法来解决问题，有时也可以另辟蹊径，结合问题特色，转变思考角度，同样也能解决问题，甚至可以优化解题策略.北京市特级教师孙维刚也经常在教学过程中向学生强调换角度思考的学习方法，换角度思考的方法经常能够帮助我们化繁为简，将未知的、陌生的问题，转化为已知的、熟悉的问题.事实上，具有换角度思考的意识和能力不仅能帮助学生更好且更快地解决问题，还能让学生更加熟悉数学知识点之间的联系，能够提高学生对数学知识体系的整体掌握程度，能够帮助学生打开视野.为了树立学生换角度思考的意识，锻炼其问题转化能力，教师要有意识地强调数学知识的体系性，打破学生思维的局限性，除此之外，教师还应该多总结能够体现换角度思考方法的问题，以教师讲解和学生练习的形式让学生清楚什么是换角度思考以及怎样更好地选取思考角度.本文中笔者将分类选取一些教学片段和经典例题来和各位读者分享自己的教学经验.

一、巧用参数分离，解决不等式求参数问题

不等式求参数问题的一般形式是给出不等式关系，求其中参数的范围，常见的思路是利用解不等式或者方程的思想来限定参数的范围，经常需要运用分类讨论的思想.在有些情况下，可以利用参数分离的方法来解决.

下题是2011年某省名校联考的试题：已知函数f（x）=xlnx，（1）试求函数f（x）的最小值；（2）如果对于∀x≥1，都有f（x）≥ax-1，试求参数a（a∈R）的取值范围.

问题分析：由于（1）比较简单，此处不作详细分析，对于（2），如果想利用不等式和函数的思想来解决，则需要先移项，构造函数g（x）=f（x）-ax+1，问题转化为对于∀x≥1，都有g（x）≥0，求此时参数a的取值范围，再利用导数求取g（x）的最小值，求出此时满足不等式条件的参数的取值范围，这样的方法可以解决本题，但此例中还需要对参数a的范围进行分类讨论，较为麻烦.其实，观察函数原型不难发现，函数的定义域是{x|x>0}，我们可以尝试换角度思考，不需要对a进行分类讨论，而是利用参数分离的方法直接求出其取值范围.

问题解答：在本题中，不等式（fx）≥ax-1恒成立等价于a≤lnx恒成立，我们只需要求出右边表达式的最小值就可以算出参数a的取值范围.构造函数h（x）=lnx+，对其求导可得，h（′x），导函数在讨论区间［1，+∞）上恒正，由此可知函数h（x）在区间［1，+∞）上单调递增，所以可得h（x）min=h（1）=1，为了使不等式恒成立，我们可以得出参数a的取值范围是（-∞，1］.

类似的例子还有很多，都显示出了参数分离的强大，再比如2009年浙江高考中有一题：已知函数f（x）=x3-（k2-k+1）x2+5x-2，g（x）=k2x2+kx+1，其中参数k∈R，设函数p（x）=f（x）+g（x），若p（x）在区间（0，3）上不单调，求参数k的取值范围.

问题分析：根据导函数的性质，如果函数p（x）在区间（0，3）上不单调，那么其导函数p′（x）=3x2+2（k-1）x+（k+5）在区间上有零点，且存在x0，x1∈（0，3），使得p（x0）≥0，p（x1）≤0，等号不同时取到，如果想通过解方程的方式求取参数的范围，计算过程将会比较繁琐，我们也可以采用参数分离的方法来求解.

问题解答：由导函数等于零，故可以分离参数，将问题转化为求在区间（0，3）上的取值范围，利用换元以及对勾函数的性质，我们可以求得k∈（-5，-2］，又当k=-2时，不存在x0，x1，使得p（x0）·p（x1）＜0，所以舍弃这一值，最终k的取值范围是k∈（-5，-2）.

二、用函数的思想研究集合

集合是中学数学的重要知识模块，高考中建立在集合基础上的考题也很多，在研究集合类题目的时候，我们可以多从函数的角度思考，跳出集合思维的限制.下面是笔者想分享的一段教学实况.

问题情境：若已知两个集合A，B，A={x|x2-3x+2＜0}，B={x|x2-ax+2＜0}，且已知A∩B=A，试求参数a的取值范围.

问题分析：这道题表面上是建立在集合的基础之上的，实际上是需要学生利用集合关系将其转化为函数来分析问题，是一道“披着集合皮的函数题”，学生需要能够跳出集合思维的限制，将集合关系转化为函数概念，从解决函数问题的角度思考.

教学情境：笔者在给出这道题目之后，让学生自行思考了一会儿，接着让其分享自己的思考过程.

学生A：“我先解出了第一个集合中的不等式，它其实等价于A={x|1＜x＜2}，然后根据集合交运算的性质，我知道了集合A是集合B的子集，也就是所有集合A中的元素都在集合B中，然后我就有点不知道怎么做了.”

教师：“很好，要解这道题，我们确实先要从集合的角度来理解条件，但是接下来的求解过程用集合的知识仿佛难以展开，那我们不妨试试转变角度，用别的知识点来思考，比如，这个集合给出的限定条件是不等式，你们能不能试试看在坐标轴上表示集合A和集合B中的元素的分布情况呢？”

学生B：“我知道了！我们可以把问题转化为函数的零点问题，因为给出的两个限定条件都是开口向上的抛物线，我们只需要确保函数f（x）=x2-ax+2的两个零点x1，x2满足条件x1≤1，x2≥2，求出此时参数a的取值范围就可以了.”

教师：“非常棒！用这样的方式解决这道题会十分轻松，这道题的求解过程可以分成两个阶段，第一个阶段是在集合视角下来解读条件，第二个阶段是用函数知识来求解答案，集合的限定条件常常以函数或不等式的形式出现，这提示我们要根据解题目标和问题特点灵活地转换解题视角，下面就请各位同学尝试着解决这道题.”

三、化抽象为形象，用数形结合的视角解决函数问题

函数能帮助我们忽视客观现象的杂芜，直接揭示蕴于其中的数学关系，大多数时候函数是一个强大且有力的工具，但是有时单纯从函数的视角下来研究问题会显得较为抽象，解决过程也会比较繁琐，这时候我们不妨借助函数图像，由形至数，形象直观地感悟问题，则可能会取得很好的效果.

比如有这样一道例题：若已知方程y=1与y=x2-|x|+a有四个公共解，求参数a的取值范围.

问题分析：一般来说，方程的公共解问题可以通过联立方程组来解决，但是本题中，y=x2-|x|+a不是我们所熟悉的方程类型，故难以求解，这时候我们不妨转变思考角度，用数形结合的思维来分析这个问题，有序数对（x，y）可以看成是坐标系中的点，方程组的公共解实际上可以等价为曲线的交点，此时问题可以转化为直线y=1与曲线y=x2-|x|+a有四个交点，作出两条曲线的难度远小于求出公共解，再通过分离参数，即可很快地求得结果.

问题解答：问题可以转化为曲线y=x2-|x|与直线y=1-a有四个交点，如图1所示作出曲线的图像.

再比如我们常见的方程零点问题，也可以用数形结合的思维来分析，如下题.

如果关于x的方程x2+（m+2）x+3=0有两个均大于1的零点，试求参数m（m∈R）的取值范围.

问题分析：以函数的思想来分析该题，我们需要解出方程的根，但由于方程中含有未知参数，若利用判别式法解题时会出现根号，求解较为繁琐，因此我们可以尝试通过参数分离的方法将问题简化，再利用数形结合的思想来求解该问题.

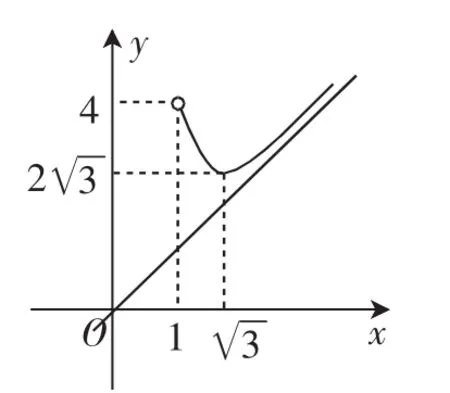
图2

问题解答：首先经过移项，我们可以得到方程-（m+2）=x+，再画出y=x+的图像（如图2），观察函数y=-（m+2）在什么情况下会与曲线有两个交点，求出此时参数的取值范围即可，易知参数需满足2（m+2）＜4，即-6＜m＜-2-2

当然，换角度思考的例子还有很多，笔者在这里只列举出了几个较为典型的案例.通过上述例题，我们能够直观地感受到换角度思考带来的便利.教师在日常教学中应有意识地让学生多接触这样的例题，鼓励学生提出新颖的思考视角，帮助学生保持思维的活跃，让他们在遇到棘手的问题或者陌生的问题时能够灵活应变，同时多进行这种转变思维的练习，能让学生感受到数学的魅力，激发起学生探索的欲望，拓宽学生的数学视野，提升他们的知识迁移应用能力，这也对其将来的学习有着深远的积极影响.