众里寻它千百度——2018年高考全国Ⅲ卷第22题

☉江苏省丹阳市吕叔湘中学 杨伟波

我国南宋时期杰出的数学家杨辉曾说：“夫学算者，题从法取，法将题验，凡欲明一法，必设一题.”其实，在教材中所选用的例题、练习题都是经过专家们再三选取、提炼而来的，能帮助我们有效地明晰概念、掌握方法.充分感受教材中所选用的例题、练习题中丰富的内涵，从而达到举一反三的目的，提高分析问题和解决问题的能力.

一、高考真题

【高考真题】（2018·全国Ⅲ卷文、理·22）在平面直角坐标系xOy中，⊙O的参数方程为为参数），过点（0，-）且倾斜角为α的直线l与⊙O交于A，B两点.

（1）求α的取值范围；

（2）求AB的中点P的轨迹的参数方程.

本题以参数方程与普通方程的互化为问题背景，通过直线与圆的位置关系、中点弦问题来考查化归与转化思想、运算求解能力以及数学运算与直观想象等数学核心素养.其实，本题在教材中有其身影，是在教材习题的背景下加以转化与拓展而来的.

二、教材背景

这个问题源于普通高中课程标准实验教科书《数学·选修2—1·A版》（人民教育出版社，2007年2月第2版）第81页习题2.5A组第4题：

过原点的直线与圆x2+y2-6x+5=0相交于A、B两点，求弦AB的中点M的轨迹方程.

三、官方标答

（1）⊙O的普通方程为x2+y2=1.

（2）方法1：

设A，B，P对应的参数分别为tA，tB，tP，

点评：第（2）小题中AB的中点P的轨迹的参数方程的求解，借助直线l的参数方程以及参数方程的几何意义下对应的参数，结合参数方程与普通方程的转化，采取根与系数的关系，并结合中点坐标公式，通过三角恒等变换的转化来确定点P的轨迹的参数方程.其实，求解第（2）小题中AB的中点P的轨迹的参数方程时，切入点各异，方法众多.

四、解几思维

除了利用参数思维或利用参数方程的几何意义来处理外，还可以借助问题本质，还原解析几何背景，通过解析几何中的直线斜率、勾股定理、圆的方程等不同的破解角度来切入，达到巧妙利用解析几何思维来处理问题的目的.

（1）方法2：

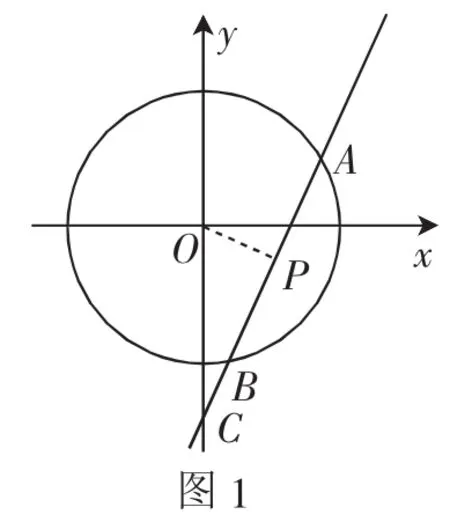
由题知⊙O的普通方程为x2+y2=1，设点（0，-）为C，如图1所示，连接OP，由于P是AB的中点，则有OP⊥AB.

即x2+y2+y=0，而当点P是O点时，也适合以上方程.

方程x2+y2+y=0表示圆，与圆x2+y2=1的公共弦所在的直线方程为y=-1，

点评：通过平面几何中的垂径定理，利用解几法中的直线的斜率公式，将垂直关系转化为直线的斜率关系来确定对应的P（x，y）的轨迹方程，根据两圆相交弦所在的直线方程并结合图形直观地来确定参数y的取值范围，进而把对应的普通方程转化为对应的参数方程即可解决.

（2）方法3：

由题知⊙O的普通方程为x2+y2=1，设点（0，-）为C，如图1所示，连接OP，由于P是AB的中点，则有OP⊥AB.

设P（x，y），由|OP|2+|PC|2=|OC|2，可得x2+y2+x2+（y+）2=（）2，

即x2+y2+y=0.

方程x2+y2+y=0表示圆，与圆x2+y2=1的公共弦所在的直线方程为y=-1，

点评：通过平面几何中的垂径定理，利用解几法中的勾股定理公式，根据两点间的距离公式来确定对应的P（x，y）的轨迹方程，并结合两圆相交弦所在的直线方程以及图形直观地来确定参数y的取值范围，进而把对应的普通方程转化为对应的参数方程即可得以解决.

（3）方法4：

由题知⊙O的普通方程为x2+y2=1，设点（0，-）为C，连接OP，由于P是AB的中点，则有OP⊥AB.

即x2+y2+=0.

点评：通过平面几何中的垂径定理，利用解几法中的圆的方程的确定，结合圆的标准方程来确定对应的P（x，y）的轨迹方程，并结合点P在⊙O内直观地来确定参数y的取值范围，进而把对应的普通方程转化为对应的参数方程即可得以解决.

五、总结分析

其实，从以上众多的破解方法中可以充分感受到中点弦问题的魅力，这也是高考中一个经常考查的热点问题.实际上，充分挖掘课本知识，感受教材中所选用的例题、练习题的底蕴，可以很好地拉近习题与高考之间的距离，并架起相应的桥梁，这也是平时数学教学与学习的一个关键所在.W