从三角问题解法错误上进行的探究性教学思考

☉安徽省临泉第二中学 刘 帅

帮助学生修正学习中的错误是教师的教学日常，因此，帮助学生有效认识错因并修正错误也就成了教师教学中的重大任务.很多教师在实际教学中喜欢采取直接告知的方式来纠正学生的错误，但这样的教学行为却往往无法收到教师预期的教学效果.事实上，教师准确把握学生的错误及原因并因此启发学生反思错因、探究错误的修正方法，才能真正使学生学有所获.

以下是笔者在学生的一些错误练习上进行的探究性教学，围绕学生的解法与错误所展开的教学简录.

一、课堂简录

1.凸显矛盾并制造问题

问题1：已知2cosx=1+sinx，求

（笔者在讲评之前打印了学生的四种解法并发给了学生，这四种解法都具有一定的代表性.）

解法1：两边平方，得4cos2x=（1+sinx）2.

因为cos2x=1-sin2x，所以4（1-sin2x）=（1+sinx）2，

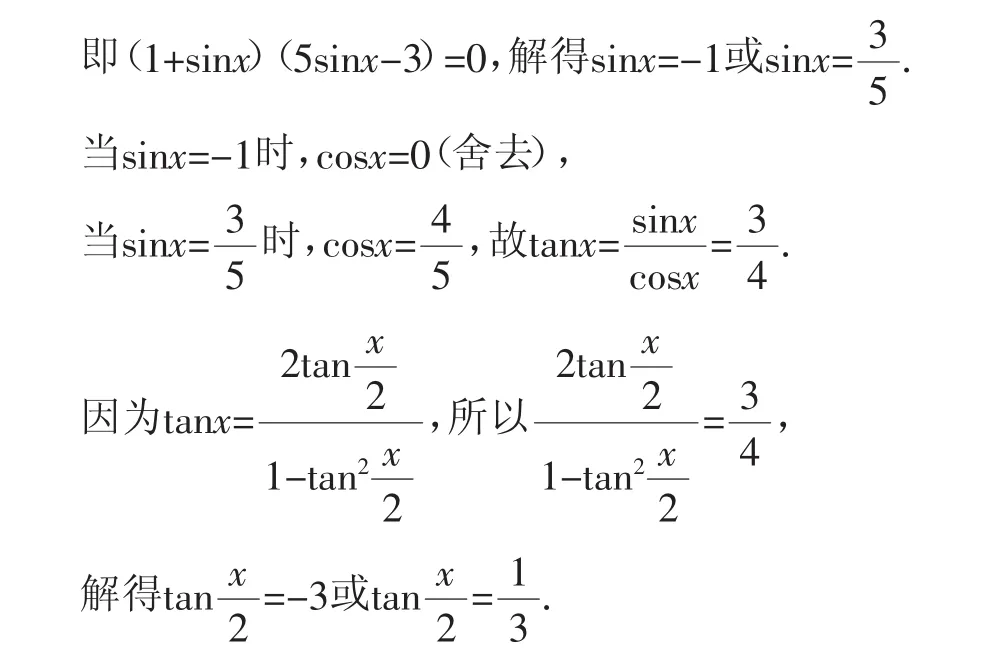
解法2：因为，所以2cosx=+sinx，两边同除以cosx得+tanx，解得tanx=

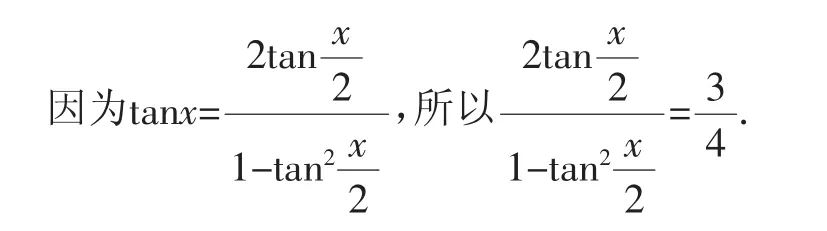
2.揭示矛盾并探究问题

师：大部分同学在本次练习中的表现都很好，现在请大家对以上四种解法进行认真的研究并阐述一下自己的想法.

（有意识地请运用解法1的学生代表首先进行了阐述）

生1：我运用的是解法1，我认为自己做得没错，不过对于解法3、解法4中出现的“-1”这个答案，我感到困惑.

师：你在解答过程中舍去了当sinx=-1时的情况，你这样做的理由是什么呢？

生1（理直气壮）：因为当sinx=-1时，cosx=0，因此可知tanx没有意义，利用二倍角的正切公式求是行不通的，因此将这一情况舍去.

（大家纷纷点头并表示赞赏）

师：很好，由以上讨论可知，解法2是不正确的，那么大家对于解法2的错误之处能进行仔细地分析吗？

生4：在解法2中，两边同除以cosx的过程中漏掉了cosx=0这一情况的讨论，因此将-1这个解遗漏了.实际上，当cosx=0时，sinx=-1，等式成立，根据解法1可得=-1；由求时，解法1中的错误就再次发生了.

师：你的分析很到位，太棒了！大家再对解法3和解法4进行一下研究吧，看结果是对的，那解题过程是否有问题？

生5：两种解法都对且在运算上显得很简洁.

师：大家的分析都很棒，大家比较一下这些解法并谈谈收获吧.

生6：解法3和解法4目标明确且运算简单，漏解和多解的现象也不易发生.

生7：方程的思想在以上四种解法中都得到了很好的运用.

（学生在分析、比较并收获解题心得后表现得更加积极.）

3.积极实践并深化认识

师：在三角函数的范畴中，角的范围对三角函数的取值往往能起到决定性的影响，三角函数的值对于角的范围也同样会起到决定性的作用.大家在解决涉及角的范围、三角函数取值之类的问题时一定要把握好两者之间的关系，把握好这一制约关系能使大家对题目形成更深层次的挖掘，很多错解也就能够得到很好的避免.

二、教学感悟

单纯的正面示范与反复练习在纠错中无法取得更好的效果，学生的“自我否定”往往能使其在产生内在的“观念冲突”时形成更好的思维，很多批判性的思维也会因此形成.

很多老师在平时教学中都会感觉较难搜集探究性学习的资料，事实上，很多的资料上提供的探究性学习材料与实际教学是无法有机衔接的，很多老师和学生面对这些材料时往往感觉无从下手，费时费力的同时也无法达到预期的教学效果.笔者认为，很多探究性学习的材料就在我们时时处处的留心之处，只要教师能够处处留心，就会发现很多能够促进学生理解力提升、问题意识形成、想象力和创造力发展的探究性学习材料.当然，教师在发现这些材料之余，还应注意材料内容、难度与学生已有知识的契合程度，恰当地把握材料的知识范畴与难度，才能令学生真正得到发展.事实上，学生的作业错误、测试错误、课堂生成问题等等都是教师可以好好利用的探究性材料.学生面对这些探究性学习材料时往往能结合自身的经验、认知能力进行新的审视与分析.本文所进行的解题探究就是在学生的解题错误上所形成的，具有初步解题思考的学生在面对解题错误时所产生的思考令人欣慰.学生在这样的探究过程中也更加具有自主参与和探究的热情，静态的知识也会因此顿时变得活跃，学生的自主发现与知识构建也因此变得积极而有意义，课堂活动充满张力与激情.

总之，学生在自主参与数学活动的过程中往往会经历更多的思考与体验，正确体验与错误体验不断交替出现的过程也将学生的问题一一暴露出来，学生的错误观念得到彻底纠正的同时也会因此形成正确的认知.因此，教师在平时教学中应善待学生的解题错误，在学生的解题错误上设计探究性活动并令学生全身心地投入到数学活动的思考、分析、反思与总结过程中.W