焦点之弦，灵巧善变

☉山东省济南市莱芜第一中学 黄 娜

抛物线的焦点弦问题一直是高考中的热点问题之一，常考常新，变化多端.解决此类问题，往往要熟练掌握抛物线的定义、方程、几何性质等内容，并结合其他相关的知识点加以综合与交汇，有时还要熟记一些焦点弦的常见的结论或公式，以便快速有效地解题，提升解题效率，优化解题过程.

一、问题呈现

【问题】（2019届高三烟台市一模·11）已知以点F为焦点的抛物线C：y2=4x上的两点A、B，满足≤ λ≤3），则弦AB的中点到抛物线C的准线的距离的最大值是（ ）.

二、多解剖析

分析1：根据抛物线的方程确定相应的焦点与准线方程，结合平面向量的线性关系确定对应线段的关系，利用抛物线的定义建立A、B两点的横坐标的关系式，求出对应横坐标的表达式，借助抛物线的定义确定弦AB的长度关系式，结合双勾函数的图象与性质确定最大值，进而求解弦AB的中点到抛物线C的准线的距离的最大值问题.

解法1：由抛物线C：y2=4x，可得p=2，则其焦点坐标为F（1，0），准线方程为x=-1.

设A（x1，y1），B（x2，y2），由，可得，

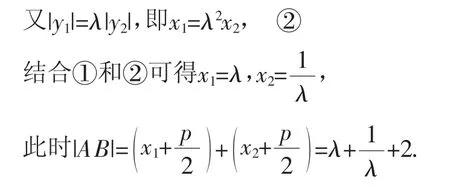
故选择答案：B.

分析2：根据抛物线的方程确定相应的焦点与准线方程，设出相应点的坐标以及直线AB的方程，并与抛物线方程联立，确定y1+y2与y1y2的关系式，结合平面向量的线性关系确定y1=-λy2，结合代数式的巧妙转化并借助双勾函数的图象与性质来确定m2的取值范围，进而通过抛物线的定义来确定弦AB的中点到抛物线C的准线的距离的关系式，进而结合m2的取值范围来确定弦AB的中点到抛物线C的准线的距离的取值范围，最终得以确定最大值问题.

解法2：由抛物线C：y2=4x，可得p=2，则其焦点坐标为F（1，0），准线方程为x=-1，

设A（x1，y1），B（x2，y2），弦AB的中点M（x0，y0），

设直线AB的方程为x=my+1，与抛物线C：y2=4x联立，可得y2-4my-4=0，

则有y1+y2=4m，y1y2=-4.

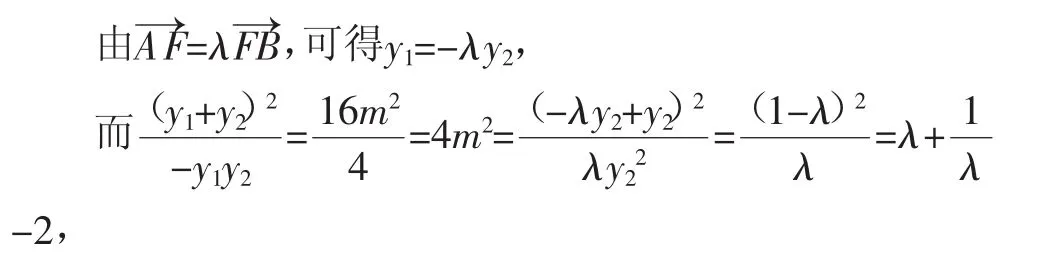
结合抛物线的定义知弦AB的中点到抛物线C的准线的距离为

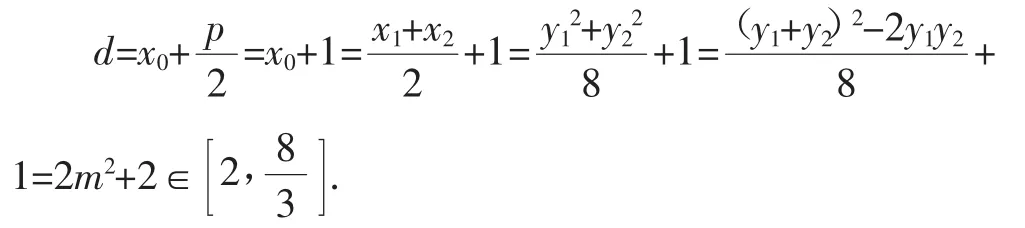
故选择答案：B.

分析3：根据抛物线的方程确定参数p的值，设出直线AB的倾斜角为θ，结合抛物线的极径公式可得|AF|与|BF|的三角关系式，结合条件中平面向量的线性关系的转化以及参数λ的取值范围来确定cosθ的取值范围，利用抛物线的焦点弦的长度公式确定|AB|的取值范围，最后再来确定弦AB的中点到抛物线C的准线的距离的最大值问题.

解法3：由抛物线C：y2=4x，可得p=2，

故选择答案：B.

三、变式拓展

探究1：保持题目条件不变，改变原来的“弦AB的中点到抛物线C的准线的距离的最大值”为“弦AB的中点到抛物线C的准线的距离的取值范围”，使得问题更为全面，难度相当.

【变式1】已知以点F为焦点的抛物线=4x上的两点A，B，满足≤ λ≤3），则弦AB的中点到抛物线C的准线的距离的取值范围是______.

解析：结合以上问题的解法2可知弦AB的中点到抛物线C的准线的距离d∈

探究2：保持题目条件不变，改变原来的参数为常数，会有不错的结论，难度相当.

【变式2】已知以点F为焦点的抛物线C：y2=4x上的两点A，B，满足（λ＞0），则弦AB的中点到抛物线C的准线的距离是______.

解析：结合以上问题的解法1可知|

由此可得两个基本的结论：

【结论1】已知以F为焦点的抛物线C：y2=2px（p＞0）上的两点A、B，满足（λ＞0），则弦AB的长度是

【结论2】已知以点F为焦点的抛物线C：y2=2px（p＞0）上的两点A，B，满足（λ＞0），则弦AB的中点到抛物线C的准线的距离是

探究3：保持题目条件不变，改变原来的“弦AB的中点到抛物线C的准线的距离的最大值”为“弦AB所在直线的倾斜角的取值范围”，转变求解角度，难度相当.

【变式3】已知以F为焦点的抛物线C：y2=4x上的两点A，B，满足≤ λ≤3），则弦AB所在直线的倾斜角的取值范围是______.

解析：结合以上问题的解法3可知

四、总结反思

其实，在平时学习与解题过程中，若涉及抛物线问题，要有意识地熟练掌握一些与之相关的技巧方法以及基本性质，特别是抛物线的焦点弦的性质，这样既有利于深入理解与掌握抛物线的定义、方程与几何性质，又能达到对相关知识的拓展与深化的目的.在破解问题时，熟练地掌握与应用常见的技巧方法与基本性质，可以减少解题时间，简化解题步骤，优化解题过程，弱化解题误区，进而全面提高数学效益，培养数学素质，提升思维品质等.W