一道预赛题的解法探究

☉上海市奉贤中学 金小蜂

☉上海市奉贤中学 王志和

2018年全国高中数学联赛福建省预赛有这样一道题：

题目已知F、F是椭圆=1（a＞b＞0）的左12右焦点，点P，1）在椭圆C上，△FPF的垂心是12

（1）求椭圆C的方程；

（2）设A是椭圆的左顶点，过F2的直线l与椭圆C交于D、E两点，记AD、AE的斜率分别是k1、k2，且满足k1+k2=，求直线l的方程.

略解：（1）椭圆C的方程为

（2）中求得直线l的斜率k=2.回顾此题的解答过程，发现，即k（k1+k2）为定值.

这激起了我们探究的兴趣，经过探究，进而得到了一些很好的结论.

结论1：已知F是椭圆=1（a＞b＞0）的右焦点， A为椭圆C的左顶点，过F且斜率是k的直线l交椭圆C于D、E两点，e为椭圆的离心率，直线AD、AE的斜率分别是k1、k2，则k·（k1+k2）=-2（1-e）.

结论1又为下述结论2的特殊情况，证明如同结论2.即我们把结论1的焦点F改成x轴上的任意一点，可以得到：

结论2：给出定点F（p，0）（p≠-a）及定点A（-a，0），过F作斜率为k（k≠0）的直线l，且与椭圆=1（a＞b＞0）交于D、E两点，直线AD、AE的斜率分别是k1、k（2k1k2≠0），则k·（

注：当A（-a，0）换成A（a，0）时，则k

证明：设直线l：y=k（x-p）并代入b2x2+a2y2=a2b2中，整理得（b2+a2k2）x2-2a2k2px+a2k2p2-a2b2=0，设D（x1，y1）、E（x2，y2），

又当p=-c时，有k·（k1+k2）=-2（1+e）.由此式及k·（k1+k2）=-2（1-e），可以得到：

结论3：已知F′、F是椭圆=1（a＞b＞0）的左、右焦点，A为椭圆C的左顶点，过F、F′分别作斜率都是k（k≠0）的直线l、l′，直线l交椭圆C于D、E两点，直线l′交椭圆C于G、H两点，直线AD、AE的斜率分别是k1、k2，直线AG、AH 的 斜 率 分 别 是 k3、k4，k1k2k3k4≠0，如图1所示，则k·（k1+k2+k3+k4）=-4.

这个式子的巧妙之处在于不论l、l′怎样运动，也不论a、b如何变化，这个定值始终是-4，真是难得！

注：此式在双曲线的情形下也有类似的结果，只要把定值-4改成4就是双曲线中对应的结论.

结论4：给出三定点F（p，0）、F′（-p，0）、A（-a，0），其中p≠±a，

过F、F′各作斜率都为k（k≠0）的直线l、l′与椭圆C：=1（a＞b＞0）分别交于D、E及G、H，直线AD、AE的斜率分别是k1、k2，直线AG、AH的斜率分别是k3、k4，0），则

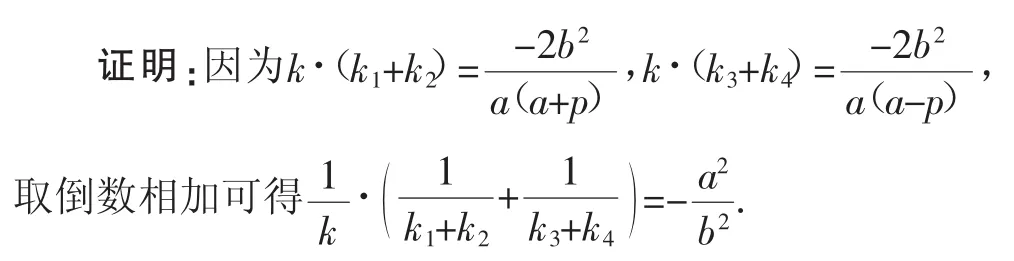
注：此处有六条动直线，且五个斜率都发生变化，而结果竟是一个定值，实属罕见.

结论5：给出定点F（0，p）（p≠-b）及定点A（0，-b），过F作斜率为k（k≠0）的直线l与椭圆=1（a＞b＞0）交于D、E两点，直线AD、AE的斜率分别是k1、k（2k1k0），则

证明：设l：x=m（y-p）（其中m=），代入b2x2+a2y2=a2b2中，整理得（b2m2+a2）y2-2b2m2py+b2m2p2-a2b2=0，设

结论6：给出三定点F（0，p）、F′（0，-p）、A（0，-b），其中p≠±b，过F、F′各作斜率都为k（k≠0）的直线l、l′，且与椭圆=1（a＞b＞0）分别交于D、E及G、H，直线AD、AE的斜率分别是k1、k2，直线AG、AH的斜率分别是k3、k4，（k1k2k3k4≠0），则

限于篇幅，对于双曲线和抛物线的相应结论在此便不再叙述.