高观点下的高考数学试题分析*

☉内江师范学院数学与信息科学学院 胡 琳

☉内江师范学院数学与信息科学学院 赵思林

“高观点”是“高观点下的初等数学”的简称，由此引申出“高观点”下的高考数学这一重要的研究课题.本文从“高观点”的角度，对高考数学试题的类型及案例做了分析，运用拉格朗日中值定理、定积分、拉格朗日乘数法等“高观点”，对一些高考数学试题做了分析.

一、有关“高观点”的研究现状

对于高考数学试题而言，“高观点”是指运用高等数学知识、方法、思想等，去分析、研究初等数学问题的一种解题策略和方法.结合“高观点”来研究高考数学问题，逐渐成为近年来高考数学研究的趋势和风向标，并且取得了大量的研究成果，如下：众所周知，菲利克斯·克莱因首次提出“高观点”，其著作为《高观点下的初等数学》；美国的JimFey指出了利用“高观点”来指导初等数学的教学过程；1989年蒋声教授提出“渗透观”；王敬庚立足变换群、拓展平面、数学方法论等“高观点”来考察解析几何；张劲松对“高观点”进行了再认识，并基于“高观点”来看待中学数学教师所处的角色；张劲松对“高观点”的内涵、理论基础、定位、在新课标中的体现等方面进行了总结；陈增武以高数的运算、概念、结论为背景，展现了高观点试题呈现出的高、低现象；赵思林从高考创新题的背景出发，研究了高数、竞赛数学等背景问题；周勇从2006年广东省高考数学压轴题中揭示了压缩映射的重要概念；范东晖研究了高考试题中数学竞赛的背景与策略；史利明用数学分析中的拉格朗日中值定理、数域概念等“高观点”对近几年的高考数学题进行了分析；蒲淑萍介绍了Klein与他的HPM思想，并给出了一定的启示；曾建国研究了高观点下关于圆锥曲线一组性质的统一，并总结了相应的命题、定理、引理等；方治结合2013年的高考数学试题来评析高考中的“高观点”；陈美茹运用柯西不等式、拉格朗日中值定理、凸函数的性质、矩阵的方法、组合数学等知识来解决数学高考题；林毅用矩阵方法解决了一类椭圆问题，以及运用洛必达法则解决了一类含参导数问题；侯代忠等从学生的解题故事出发，启发出初、高等数学两个不同角度的探究，以及展现了线性递归方程、母函数、不动点等“高观点”来研究问题的巧妙之处；王雅琪以2015年的北京高考数学的解析几何试题为例，将几何问题代数化；王雅琪以高考数学北京卷为例，考查了高考中的概率与统计问题；曹世鹏研究了以高等数学的符号和概念、以高等数学基本公式、以高等数学中的矩阵知识、以高等数学中的导数思想和积分思想等“高观点”为背景的高考数学问题；王雅琪运用极点极限的“高观点”解决了北京高考解析几何中的圆锥曲线问题；陈建华通过对新课标的解读，并结合“高观点”对行列式展开了研究；郝保国展示了数论知识渗透到高考试题中的独特魅力；张晓东从组合数学、反演变换、数论中的进位制等竞赛背景来巧解高考数学题；张永春等利用拉格朗日中值定理来解决高考中的导数问题；王珊珊立足于切比雪夫多项式视角来探究高考题与竞赛题；赵思林等从柯西不等式、凸函数的性质等高观点来对一道高考不等式题进行研究性学习.

二、“高观点”下高考数学试题的类型及案例

1.拉格朗日中值定理

例1（2017年全国Ⅱ卷文科21题）设函数f（x）=（1-x2）ex.

（Ⅰ）讨论函数f（x）的单调性；

（Ⅱ）当x≥0时，f（x）≤mx+1，求m的取值范围.

分析：借助高数知识，能够巧妙地解决高考中难度较大的导数压轴题.

解：（Ⅰ）对（fx）=（1-x2）ex求导，易得

（Ⅱ）首先，将x分成两类，

即（fx）≤mx+1.

当x=0时，成立，m∈R；

然后，判断f（x）=（1-x2）ex是否符合拉格朗日中值定理的条件.

因为f（x）=（1-x2）ex在［0，x］（x＞0）上连续，在（0，x）（x＞0）上可导，

所以存在ξ∈（0，x），使得

又f′（x）=ex（-x2-2x+1），

则f′（ξ）=eξ（-ξ2-2ξ+1），

所以f″（ξ）=-eξ（ξ2+4ξ+1）＜0.

则f′（ξ）在（0，x）上单调递减.

故f′（ξ）max=f′（0）=1.

所以m≥1.

最后，取交集，

综上所述，m的取值范围为［1，+∞）.

注：本例运用了数学分析中的拉格朗日中值定理，通过分类（如x=0和x＞0）、条件（即满足拉格朗日中值定理的前提条件）、取交集（即在分类讨论下取值范围的交集）来逐步完成对此类题的求解，但前提是不等式可以逐步构造成拉格朗日中值定理的形式，这也是数学的巧妙之处.

2.定积分

例2（2014年江西卷理科8题改编）若g（x）=2x+x）dx=______.

所以g′（x）=2.

可设g（x）=2x+c，

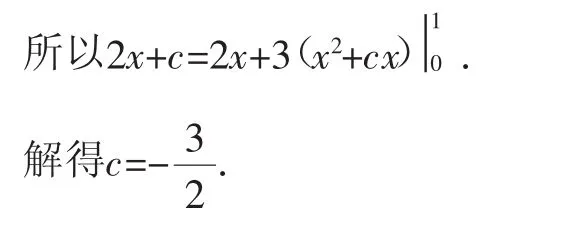
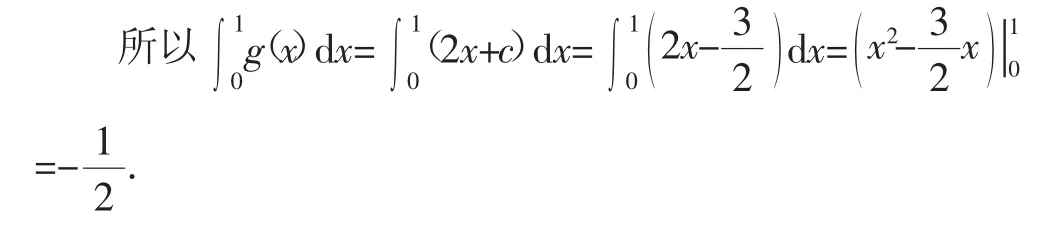
注：需要注意的是：如果定积分的积分上限和积分下限都是常数，则它的结果是一个数值.

3.拉格朗日乘数法

拉格朗日乘数法在条件φ（x，y）=0的限制下，求函数f（x）=f（y，z）的极值.对于条件极值问题，拉格朗日函数为L（x，λ）=L（y，z，λ）=f（y，z）+λφ（y，z），其中λ=（λ1，…，λm）T为拉格朗日乘数向量，依次求Lx′（x，y，λ）=0，Ly′（x，y，λ）=0，Lλ′（x，y，λ）=0，进而解出极值点（x，y）.

例3（2014年辽宁卷16题改编）∀c＞0，对于所有的实数a，b（a，b≠0）符合条件4a2-2ab+4b2-c=0，并且使|2a+b|最大时的最小值是______.

解析：因为|2a+b|2=4a2+4ab+b2，

所以构造函数L（a，b）=4a2+4ab+b2+λ（4a2-2ab+4b2-c）.

将λ消去，则有2a=3b，

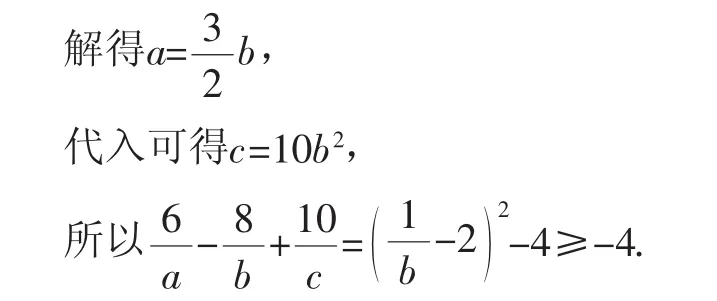
注：本例巧妙地利用了拉格朗日乘数法，便可使得多元参数的最值问题迎刃而解.

三、“高观点”数学试题的教学建议

张劲松曾提出了“高观点”的理论基础，有认识的辩证运动、下位学习、螺旋式课程等，从中可以体会到“高观点”对解决初等数学问题的独特作用.“高观点”是教学改革中的一种创新，“高观点”具有高、深、难等显著特点，高即是思维观点高、素养品质高，深即是深刻，难即是有一定难度.基于“高观点”的教学有如下建议：一是要结合要点学习、研究、思考；二是可以多搜集一些有关高观点的文献资料；三是精选案例进入课堂教学，为学生提供优良的教学案例；四是教师立足“高观点”，自己开发练习题，让学生得到好的训练；五是通过对“高观点”的学习，为学生编拟出更有价值的数学问题.“高观点”的教学，要激发学生积极思考数学问题，引起学生的学习兴趣，使学生们能举一反三，逐渐领会变式、迁移等技巧.此外，还可以鼓励并指导学有余力的尖子生学习一些高等数学.