多解赏析，变式探究——一道直线与圆的最值试题

☉山东省日照第一中学 孙 蕾

直线与圆是解析几何中的简单图形，但是它们两者间的位置关系涵盖方程与函数思想、数形结合思想等，常见的问题有位置关系问题、参数问题、弦长问题、最值问题、性质问题、动态问题等，有时也涉及相对难一点的轨迹问题，因此其一直成为各级各类考试的必考内容和热点内容，要引起重视.下面结合一道直线与圆的动态中的最值问题，采用多角度思维进行解法赏析与变式探究.

一、问题呈现

【问题】在平面直角坐标系xOy中，已知圆C：x2+（y-1）2=4，若等边△PAB的一边AB为圆C的一条弦，则|PC|的最大值为______.

本题以圆所对应的标准方程为问题背景，结合等边△PAB的一边AB为圆C的一条弦进行展开，探讨|PC|的最大值问题.由于随着弦AB的变化，要使得|PC|取得最大值，显然点P应该在弦AB异于圆心C的另一侧，且随着弦AB的变化，点P的位置也随着变化，因此如何把直线与圆的动态问题进行代数化，从而得以代数运算是解决问题的切入点.

二、多解思维

思维角度1：（直线与圆的位置关系法）取特殊情况，假设点P在y轴上，根据条件确定直线PB的倾斜角，进而设出对应的直线方程，根据条件转化已知直线PB与圆C有公共点，利用点到直线的距离公式以及绝对值不等式来确定|PC|的最大值.

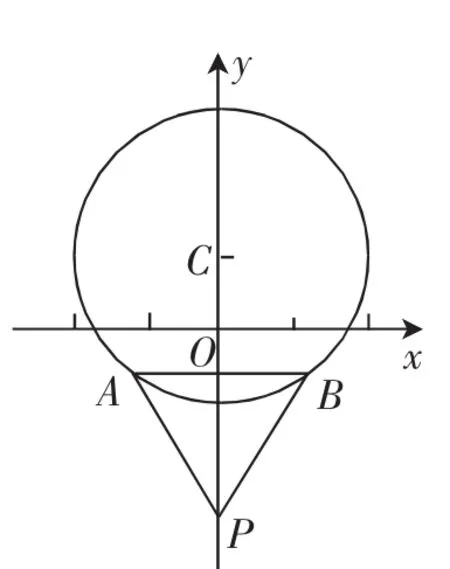
图1

解法1：由于等边△PAB的一边AB为圆C的一条弦，根据对称性可知PC⊥AB，假设点P在y轴上，设P（0，b），如图1所示，依题意可知直线PB的倾斜角为，其对应的斜率为，故设直线PB的方程为y=x+b，即x-y+b=0.根据题目条件可知直线PB与圆C有公共点，则有圆心C（0，1）到直线PB的距离≤r=2，则有|b-1|≤4，所以 |PC|=|b-1|≤4，即|PC|的最大值为4，故填答案：4.

思维角度2：（三角函数法）结合条件先确定圆C的半径r=2，利用等边△PAB的一边AB为圆C的一条弦得到PC⊥AB，设出∠ACP=α，结合三角函数的定义可得|AH|=2sinα，|HC|=2cosα，利用|PC|=|PH|+|HC|的关系式的转化，通过三角函数的辅助角公式的应用得以确定|PC|的最大值.

解法2：由题可得圆C的半径r=2，由于等边△PAB的一边AB为圆C的一条弦，根据对称性知PC⊥AB，垂足记为H，设∠ACP=α，可得|AH|=2sinα，|HC|=2cosα，那么|PC|=|PH|+|HC|=2sinα+2cosα=4sin时，即时，|PC|取最大值为4，故填答案：4.

思维角度3：（解三角形法）结合圆的对称性确定PC⊥AB，在△PBC中利用正弦定理建立相应的关系式，再通过转化得到|PC|所对应的三角关系式，利用三角函数的图象与性质来确定其最大值，此时恰好PB与圆C相切.

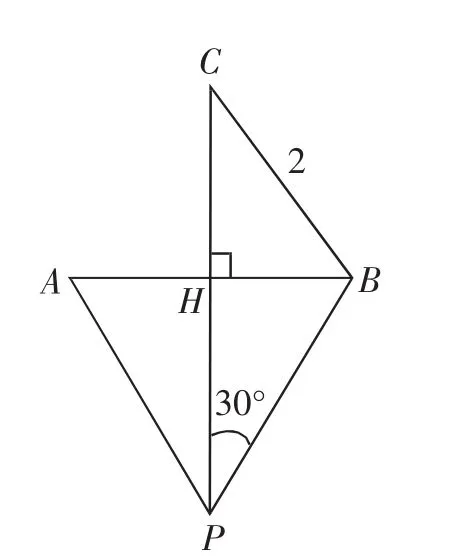
图2

解法3：由于等边△PAB的一边AB为圆C的一条弦，根据对称性知PC⊥AB，如图2所示，在△PBC中，|BC|=r=2，∠CPB=30°，由正弦定理有，可得·sin∠PBC=4sin∠PBC，则当∠PBC=90°时，此时PB与圆C相切，|PC|有最大值为4，故填答案：4.

思维角度4：（参数方程法）取特殊情况，假设点P在y轴上，并设出P（0，y0），结合圆C的参数方程，通过点B的坐标建立参数y0的关系式，并结合三角函数的辅助角公式转化为正弦函数来确定y0的最小值，进而通过数形结合来确定|PC|的最大值.

解法4：由于等边△PAB的一边AB为圆C的一条弦，根据对称性可知PC⊥AB，假设点P在y轴上，设，如图3所示，由圆C：x2+（y-1）2=4，其对应的参数方程为θ为参数），结合等边三角形的性质可知1，则当θ==1+2sinθ=0时，y取得最小0值-3+0=-3，此时|PC|的最大值为3+1=4，故填答案：4.

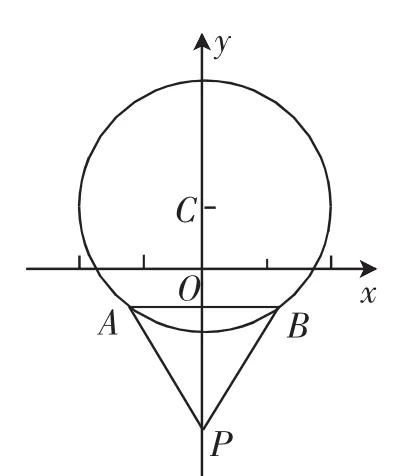
图3

思维角度5：（导数法）结合条件先确定圆C的半径r=2，利用等边△PAB的一边AB为圆C的一条弦得到PC⊥AB，设出|AB|=2t，利用s=|PC|=|PH|+|HC|得到对应的函数关系式，通过求导，结合函数的单调性来确定相应函数的极大值，也就是最大值，从而得以确定|PC|的最大值.

解法5：由题可得圆C的半径r=2，由于等边△PAB的一边AB为圆C的一条弦，根据对称性知PC⊥AB，垂足为H，设|AB|=2t，可得s=|PC|=|PH|+|HC|=0＜t＜2），而，令s′=0，解得t=，则当t∈（0，）时，s′＞0，函数单调递增；当t∈（，2）时，s′＜0，函数单调递减.

思维角度6：（柯西不等式法）结合条件先确定圆C的半径r=2，利用等边△PAB的一边AB为圆C的一条弦得到PC⊥AB，设出|AB|=2m，利用|PC|=|PH|+|HC|的关系式的转化，结合柯西不等式来确定其最值，从而得以确定|PC|的最大值.

解法6：由题可得圆C的半径r=2，由于等边△PAB的一边AB为圆C的一条弦，根据对称性可知PC⊥AB，垂足为H，设|AB|=2m，结合柯西不等式，可得|PC|=|PH|+|HC|=4，当且仅，即m=时等号成立，所以当|AB|=时，|PC|取最大值为4，故填答案：4.

三、变式探究

【变式1】在平面直角坐标系xOy中，已知圆C：x2+（y-1）2=4，若等边△PAB的一边AB为圆C的一条弦，则当|PC|取得最大值时，△PAB的面积为______.

解析：由题可得圆C的半径r=2，由于等边△PAB的一边AB为圆C的一条弦，根据对称性知PC⊥AB，垂足为H，设|AB|=2m，结合柯西不等式，可得|PC|=|PH|+|HC|=4，当且仅当，即m=时等号成立，所以当|AB|=2时，|PC|有最大值为4，此时△PAB的面积S=×3=3，故填答案：3

【变式2】在平面直角坐标系xOy中，已知圆C：x2+（y-1）2=4，若等腰直角△PAB的斜边AB为圆C的一条弦，则|PC|的最大值为______.

解析：由题可得圆C的半径r=2，由于等腰直角△PAB的斜边AB为圆C的一条弦，根据对称性知PC⊥AB，垂足为H，设∠ACP=α，可得|AH|=2sinα，|HC|=2cosα，那么|PC|=|PH|+|HC|=2sinα+2cosα=2sin），当α+时，即时，|PC|的最大值为2，故填答案：

解决此类平面解析几何中的动态问题，关键是抓住题目条件，把对应的动态问题进行有效的代数化或几何化，进而通过代数方法或几何方法来解决相应的动态问题，从而得以巧妙处理，正确破解，方法各异，奇思妙想，切入点不同，破解策略多样.其实，在处理数学中的动态问题时，合理地将动态问题静态化，然后通过代数法或几何法来处理，特别在破解一些相关的小题时是非常重要的一种解题策略，充分体现出“小题小做，小题巧做”的思想，有助于数学解题能力与应用能力的提高，从而真正提升综合能力，拓展数学素养.F