高三二轮复习专题：减元法解决导数多变元问题

☉四川省成都七中 王 华

导数是高中数学的重要内容，高考数学的压轴题也经常考查学生运用导数研究函数的综合能力.下面通过几个典型例题，说明“减元法”是解决导数压轴题中“多变元”问题的通性通法.

例已知函数f（x）=ax+lnx+1.（1）略；

（2）对任意x＞0，f（x）≤xe2x恒成立，求实数a的取值范围.

解：（2）方法一：由题意，对任意x＞0时ax+lnx+1≤xe2x恒成立，等价于）在（0，+∞）上恒成立.

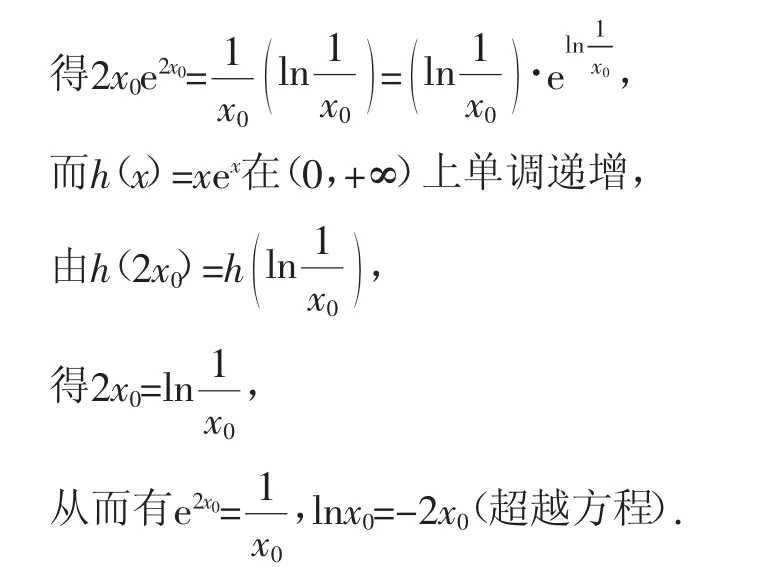
综上所述，a≤2（此方法也称为“隐零点法”，本质是消掉超越运算.）

方法二：由题意，x＞0时ax+lnx+1≤xe2x，即a≤e2x-

考题链接：1（.18届成都三诊改编）已知函数（fx）=xalnx-1，当a∈（0，1）∪（1，+∞）时，（fx）恰有两个零点x1，x2

证明：由题意得x＞0），而a∈（0，1）∪（1，+∞）.

思路一：

所以g（t）在（0，1）上单调递增，

所以当t∈（0，1）时，g（t）＜g（1）=0，

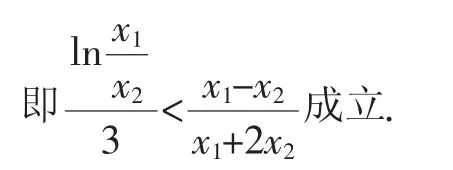
综上所述，原不等式成立.

考题链接：2（.2019届成都一诊）：已知函数（fx）=-alnx-，a∈R（.1）略.

解：（2）由题意得，当a=1时，不等式（fx）+bx≥1恒成立，

即xex-lnx+（1-b）x≥1恒成立，

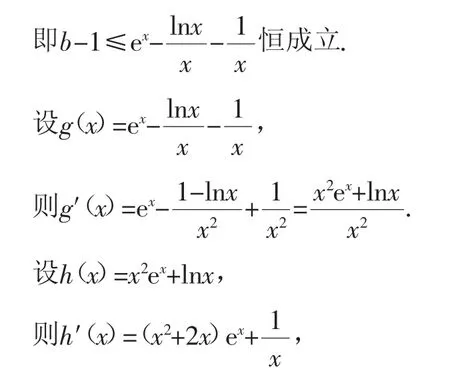
因为当x＞0时，有h′（x）＞0，

所以h（x）在（0，+∞）上单调递增，且h（1）=e＞0，-ln2＜0.

所以当x∈（0，x0）时，h（x）＜0，g′（x）＜0，g（x）单调递减；

当x∈（x0，+∞）时，h（x）＞0，g′（x）＞0，g（x）单调递增.

所以g（x0）为g（x）在定义域内的最小值.

而k（′x）=（x+1）ex＞0，对x∈（0，+∞）恒成立，

即k（x）在（0，+∞）上单调递增，

易知m（x）单调递增.

所以实数b的取值范围为（-∞，2］.

方法小结：

1.一般的多变元问题我们常考虑通过“减元法”将多变元转化为单变元进行求解.

2.“隐零点法”是通过代换，将超越形式消掉，化为普通运算.

3.文中所指的“多变元”问题，可以是广义上的，比如“隐零点法”中e2x0和lnx0的计算问题，利用方程进行消元，转化为普通多项式的计算问题，体现了化繁为简、化未知为已知的基本解题思路.

4.方程思想是“减元法”的灵魂.F