HPM视角下球体积公式推导的教学设计

☉上海市进才中学 张乐瑛

一、引言

祖暅原理是我国传统数学中的一个非常重要的成就，在数学史上它与被称为微积分萌芽的卡瓦列里定理是相媲美的；球体积公式的推导是古代几何学中的一个难题，东西方好几代数学家都竭尽智慧探求其精确公式.在沪教版高中数学教科书中由于篇幅有限，直接给出了祖暅原理以及由应用祖暅原理和长方体的体积推导出棱柱体积的结论，且对于球的体积公式仅有结论呈现.教材的安排很难让学生真正理解祖暅原理，亦感悟不到古代数学家在推导球体积公式时所迸发出的创造性的思维火花和丰富的文化内涵，因此本文将尝试从数学史的视角对祖暅原理以及球体积公式的推导进行教学设计.

二、数学史料

1.《九章算术》中的球体积公式

《九章算术》认为正方体与其内切圆柱的体积之比等于正方形和其内切圆的面积之比为4∶3（取π=3），等边圆柱与其内切球的体积之比是4∶3（如图1），于是得球与其外切正方体的体积之比为9∶16，即得公式

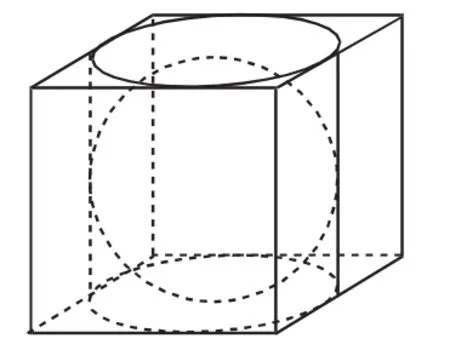
图1

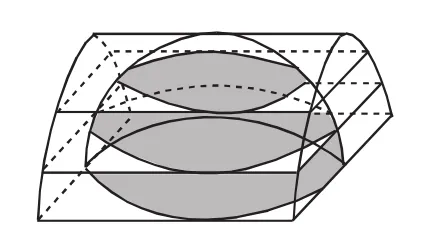
图2

2.刘徽和牟合方盖

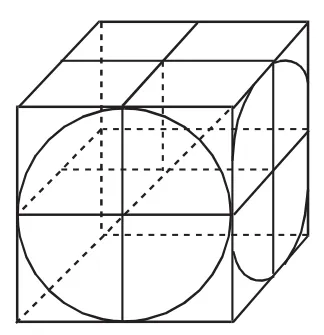
图3

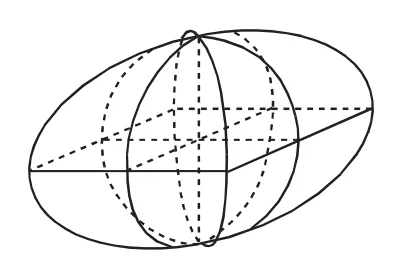
图4

牟合方盖恰好把立方体的内切球包含在内并且同其相切，因此两者的体积之比为面积之比

因为球体与牟合方盖任何一个等高的截面面积之比均为π∶4，所以可以确定球体与牟合方盖的体积之比亦为π∶4（如图5）.此时，只要求出牟合方盖的体积，球的体积便迎刃而解.

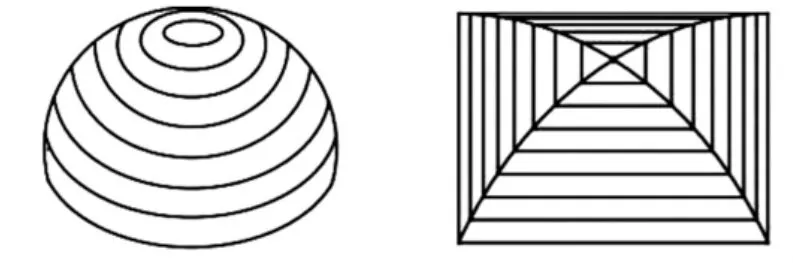
图5

3.祖暅原理和球的体积

两百年后，祖暅沿用刘徽的思想，利用牟合方盖的理论去进行体积计算.祖暅首先取牟合方盖的八分之一来进行研究，他没有直接求八分之一牟合方盖的体积，转而研究从八分之一小正方体中扣除八分之一牟合方盖后的剩余几何体的体积.按常规说来，剩余几何体形状不规则，更不易求，但祖暅用平行于底的平面在高h处截八分之一正方体与牟合方盖，发现截面在立方体内且在牟合方盖外的部分由勾股定理计算可得面积S阴影=r2-（r2-h2）=h2（如图6），且底边为r，高也为r的倒立方锥在高h处的截面面积亦为h2，于是他发现两个等高的几何体在任意等高处的横截面面积相同，即祖暅原理——缘幂势既同，则积不容异，根据这一结论，通过计算得出V剩余=V倒立锥，V牟合方盖=牟合方盖=故得出

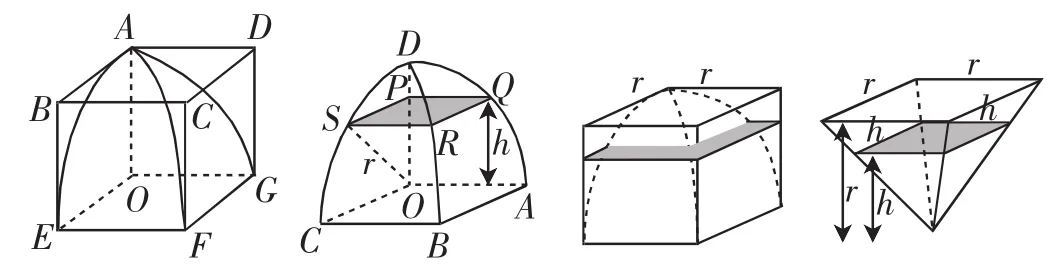
图6

三、教学设计与实施

1.回顾历史，提炼思路

教师：这节课首先让我们跟随前人探索和发现的脚步去重温古人是如何推导出球体积公式这段历史的.

学生阅读材料.

教师：从材料中我们可以看到，当古人探索球体积这个新问题时，他们是怎么做的？

生1：将球的体积问题和正方体、圆柱的体积联系起来.在高度相同的情况下，研究他们相切的面积之比作为体积之比.

教师：如果说面积是二维的，那么体积就是三维的，我们可以将体积问题向面积问题转化，这里体现了一种什么解决问题的方法？

生2：降低维度，就是将复杂向简单转化.

教师：祖暅沿用了刘徽的思想，他第一个聪明的地方是将原来的“牟合方盖”平均分为八份，取它的八分之一来研究.为什么可以这样做？

生3：因为对称性.

教师：祖暅第二个聪明的地方在于他没有直接求八分之一牟合方盖的体积，转而求从小正方体中扣除八分之一牟合方盖后的剩余体积.祖暅根据直觉和经验提出祖暅原理，今后可以用微积分知识证明.通过短短的回顾球体积公式推导的历史，我们看到了凝结在数学公式背后的努力和智慧，探索和突破，谈谈你印象最深刻的地方.

生4：刘徽的质疑和牟合方盖的构造，祖暅的分解难点和转化困难寻找突破的智慧.

2.应用原理，推导体积

教师：在这里最核心的就是祖暅原理，同学能把这个定理中的关键点提炼出来吗？

教师板书：祖暅原理：两个几何体

（1）等高；

（2）任意高度截面面积相等；

（3）转化为已知或者易求体积的几何体.

教师：今天我们能否尝试和古人一样从已知体积的几何体出发推导球的体积呢？想一想，我们前面学习了哪些几何体的体积？如果想运用祖暅原理，必须是两个几何体同底等高，但球没有底，我应该如何构造与它同底面的几何体？

生5：我们已知圆柱、圆锥的体积，由球的对称性，取二分之一的球体计算，半球是有底面的几何体.

教师：在祖暅原理中，除了高度相同，我们要关注截面的面积是否相同，在不知道用什么几何体来和半球对比时，我们可以从球的截面面积公式中寻找灵感，若已知球的半径为r，则用与底面平行且高度为h的平面截球所得的截面形状是什么？截面面积为多少？

生6：截面形状为圆，截面面积S=πr2-πh2.

教师：这样的形式，我们想到什么图形的面积会是这样？

生7：圆环.两个同心圆，大圆的半径为r，小圆的半径为h，大圆中挖去小圆形成圆环.

教师：如果球是确定的，则半径r是常数，而h是随着截面高度变化而变化的.根据祖暅原理，下面我们该怎么做才能求出半球的体积.

生8：要找一个几何体和半球等高，高度h的截面面积为S=πr2-πh2，一个圆柱去掉一个圆锥.底面半径为r的圆柱、高（迟疑之际，同学提醒：等高）也为r，底面半径和高均为r的圆锥.

教师：（画出正立圆锥）是这样的吗？距离底面距离为h的截面的面积是πh2？

生9：不是，应该是π（r-h）2.应该是倒立的圆锥！

教师：（画出倒立的圆锥）此时距离底面距离为h的截面的面积是πh2，你怎么想到的？

生10：祖暅想到的！所以根据祖暅原理，半球的体积等于圆柱的体积减去圆锥的体积，相当于是一个圆柱中挖去底面积相等，高度相同的圆锥（图7）大家鼓掌！

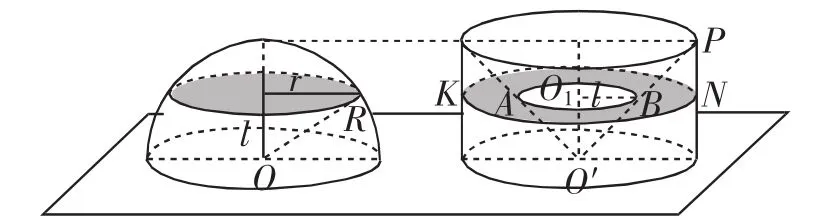
图7

教师：同学们通过对祖暅原理的学习，能够将体积求解的关注点放在截面上进行观察，从而通过截面的特征看到几何体的构造.今天我们站在巨人的肩膀上，用传统数学上的很重要的结论——祖暅原理，在短时间内完成了古人三百年探求的结论，说明我们只有跟随前人探索和发现的脚步，才能将前人思考和突破的方法进行借鉴与创新.

3.理解思路，应用巩固

教师：我们都知道球体可以看做是圆面绕直径旋转而成的旋转体，如果椭圆绕对称轴旋转一周是一个椭球，那么你能尝试求出来椭球的体积吗？

例1 请在研究和理解球的体积公式求法的基础上，解答问题：已知椭圆的标准方程为1，将此椭圆绕y轴旋转一周后，得一橄榄状的几何体，求其体积.

生11：先研究在x轴上方的椭圆绕y轴旋转所得的半个椭球的体积.

平行于x轴，且距离为y（y＞0）的直线交椭圆第一象限部分的交点为则对应平面截得椭球的截面是一个圆，面积为这个截面也可以看做是一个圆环，两个同心圆，大圆半径为2，小圆半径为

根据祖暅原理，可构造几何体，从一个圆柱中间挖去一个倒立的圆锥.所以椭球的体积为

教师：很好，该同学不仅正确地解决了这个问题，而且思路清晰，并将这类问题的解决步骤规范化，值得我们大家学习.（鼓掌）

四、结语

本节课属于重构式的HPM教学案例，通过探寻数学历史中球的体积公式的发展脉络，从刘徽到祖暅，从球的体积到祖暅原理，让学生经历探究过程，感受古人在探究过程中的非凡智慧和探索精神.同时，将前人的结论进行借鉴和创新，尝试后获得成功的快乐.本教案在设计和实践中，有如下感悟：

1.教学实践中应选择合适的数学史融入教学

我们在数学教学中经常会遇到学生有这样的问题：为什么要学这个定理？它是怎么想到的？本节课根据教学内容选择了重构式，重现刘徽构造牟合方盖推导球的体积，祖暅提出祖暅原理得到球体积公式的完整过程.数学史的运用使定理的出现合理自然，同时也解决了对祖暅原理的内涵理解，应用方式等教学难点.数学教材需要保证知识的系统性，但也容易让学生认为数学学习是靠死记硬背的方式去学习一些孤立的知识，解决这一矛盾的有效途径之一是适当地将数学史融入日常教学中，做到既让学生学习到系统的数学知识，又让学生清晰地了解和认识到数学知识的产生过程，养成良好的思维方式，从而为创新思维的培养做好铺垫.

2.教学实践中应重视数学史中蕴含的数学思想和教育功能

科学家傅鹰教授有一句名言“科学只给我们知识，而历史却给我们智慧”.在学科学习中，了解知识的发展历程，可以促进我们正确地理解科学本质.在球的体积公式的推导过程中，首先多次运用到转化思想，如《九章算术》中公式虽然不对，但古人将空间问题转化为平面问题处理的转化思想蕴含其中；其次在推导过程中构造的思想方法亦不断出现，学生印象最深刻的是祖暅将未知几何体的体积与倒立正方锥的体积对等，在后面构造几何体推导半球体积中根据截面面积S=πr2-πh2学生自然想到倒立的圆锥，教学难点不攻自破；最后，无论在刘徽构造牟合方盖还是祖暅提出祖暅原理的过程中都蕴含着极限思想，从直到曲，从有限到无限，虽然没有明确提出极限的概念，但是让学生感受到极限的思想.

在历史重构过程中学生经历了古人揭开数学奥秘的艰辛历程，经历了令人振奋的探索过程，为刘徽和祖暅的智慧而惊叹，为数学家敢于坚持真理的钻研精神而心生敬佩，为古代数学的辉煌成就而感到自豪，从而激励学生为科学的发展而努力学习.